文章目录
- 一、导数与微分
- 1.导数的概念
- (1)导数的定义
- (2)左右导数
- (3)定理:可导与左右导数的关系
- (4)可导三要素
- (5)用导数定义判断可导性
- 2.微分的概念
- (1)微分的定义
- (2)微分与可导的关系
- 3.导数与微分的几何意义
- (1)导数 f ′ ( x 0 ) f'(x_0) f′(x0)的几何意义:切线的斜率、相关变化率
- (2)微分的几何意义:切线的增量
- 4.连续、可导、可微之间的关系
- 5.导数公式
- 6.求导法则
- (0)结论:奇偶性、周期性、分段函数分段点
- (1)有理运算法则
- (2)复合函数:链式求导法则 (链导法)
- (3)隐函数求导法
- (4)参数方程求导法
- (5)反函数的导数
- (6)对数求导法
- (7)高阶导数
- 二、微分中值定理与导数应用
- 1.微分中值定理
- (0)费马引理
- (1)罗尔定理
- (2)拉格朗日中值定理
- (3)柯西中值定理
- (4)泰勒中值定理 (泰勒公式拉格朗日余项)
- 总结
- 微分中值定理的证明题
- (1)单中值:证明存在一个点ξ∈(a,b),使 g [ ξ , f ( ξ ) , f ′ ( ξ ) ] = 0 g[ξ,f(ξ),f'(ξ)]=0 g[ξ,f(ξ),f′(ξ)]=0
- (2)双中值:证明存在两个中值点 ξ,η∈(a,b),使 g [ ξ , η , f ( ξ ) , f ( η ) , f ′ ( ξ ) , f ′ ( η ) ] = 0 g[ξ,η,f(ξ),f(η),f'(ξ),f'(η)]=0 g[ξ,η,f(ξ),f(η),f′(ξ),f′(η)]=0
- (3)高阶导数:证明存在一个中值点 ξ∈(a,b),使 g [ ξ , f ( n ) ( ξ ) ] ≥ 0 ( n ≥ 2 ) g[ξ,f^{(n)}(ξ)]≥0 \ (n≥2) g[ξ,f(n)(ξ)]≥0 (n≥2)
- 2.泰勒公式
- (1)泰勒中值定理1:佩亚诺余项,局部泰勒公式,用于极限的计算
- (2)泰勒中值定理2:拉格朗日余项,整体泰勒公式,用于证明
- (3)麦克劳林公式
- 3.单调性与极值、最值
- (1)函数的极值
- (2)函数的最大值、最小值
- 4.曲线的凹凸性与拐点
- (1)凹凸性
- (2)拐点
- 5.曲线的渐近线
- ①水平渐近线 (双向)
- ②铅直渐近线 (找无穷间断点)
- ③斜渐近线 (双向)
- 快速求斜渐近线
- 6.平面曲线的曲率
- 7.方程的根:存在性、个数
- 8.函数不等式的证明
- (1)证明不等式的5种常用方法
- (2)基本不等式
一、导数与微分

1.导数的概念
(1)导数的定义
(1) f ′ ( x 0 ) = lim Δ x → 0 Δ y Δ x = lim Δ x → 0 f ( x 0 + Δ x ) − f ( x 0 ) Δ x = lim h → 0 f ( x 0 + h ) − f ( x 0 ) h f'(x_0)=\lim\limits_{Δx→0}\dfrac{Δy}{Δx}=\lim\limits_{Δx→0}\dfrac{f(x_0+Δx)-f(x_0)}{Δx}=\lim\limits_{h→0}\dfrac{f(x_0+h)-f(x_0)}{h} f′(x0)=Δx→0limΔxΔy=Δx→0limΔxf(x0+Δx)−f(x0)=h→0limhf(x0+h)−f(x0)
(2) f ′ ( x 0 ) = lim x → x 0 f ( x ) − f ( x 0 ) x − x 0 f'(x_0)=\lim\limits_{x→x_0}\dfrac{f(x)-f(x_0)}{x-x_0} f′(x0)=x→x0limx−x0f(x)−f(x0) 【 Δ x = x − x 0 ⇨ x = x 0 + Δ x Δx=x-x_0 ⇨ x=x_0+Δx Δx=x−x0⇨x=x0+Δx】
(3)
f
(
x
)
f(x)
f(x)在
x
=
0
x=0
x=0处可导
⇔
\Leftrightarrow
⇔
lim
x
→
0
f
(
x
)
−
f
(
0
)
x
\lim\limits_{x→0}\dfrac{f(x)-f(0)}{x}
x→0limxf(x)−f(0)存在
若
f
(
0
)
=
0
f(0)=0
f(0)=0,则
f
(
x
)
f(x)
f(x)在
x
=
0
x=0
x=0处可导
⇔
\Leftrightarrow
⇔
lim
x
→
0
f
(
x
)
x
\lim\limits_{x→0}\dfrac{f(x)}{x}
x→0limxf(x)存在
①导数是一种特殊的极限,导数是函数改变量与自变量改变量之比的极限(变化率的极限存在)。
②导数 刻画 函数在这一点的变化率。
(2)左右导数
①左导数的定义:
f
′
_
(
x
0
)
=
lim
Δ
x
→
0
−
Δ
y
Δ
x
=
lim
Δ
x
→
0
−
f
(
x
0
+
Δ
x
)
−
f
(
x
0
)
Δ
x
=
lim
x
→
x
0
−
f
(
x
)
−
f
(
x
0
)
x
−
x
0
f'\_(x_0)=\lim\limits_{Δx→0^-}\dfrac{Δy}{Δx}=\lim\limits_{Δx→0^-}\dfrac{f(x_0+Δx)-f(x_0)}{Δx}=\lim\limits_{x→x_0^-}\dfrac{f(x)-f(x_0)}{x-x_0}
f′_(x0)=Δx→0−limΔxΔy=Δx→0−limΔxf(x0+Δx)−f(x0)=x→x0−limx−x0f(x)−f(x0)
②右导数的定义:
f
+
′
(
x
0
)
=
lim
Δ
x
→
0
+
Δ
y
Δ
x
=
lim
Δ
x
→
0
+
f
(
x
0
+
Δ
x
)
−
f
(
x
0
)
Δ
x
=
lim
x
→
x
0
+
f
(
x
)
−
f
(
x
0
)
x
−
x
0
f'_{+}(x_0)=\lim\limits_{Δx→0^+}\dfrac{Δy}{Δx}=\lim\limits_{Δx→0^+}\dfrac{f(x_0+Δx)-f(x_0)}{Δx}=\lim\limits_{x→x_0^+}\dfrac{f(x)-f(x_0)}{x-x_0}
f+′(x0)=Δx→0+limΔxΔy=Δx→0+limΔxf(x0+Δx)−f(x0)=x→x0+limx−x0f(x)−f(x0)
(3)定理:可导与左右导数的关系
(1)可导
⇔
\Leftrightarrow
⇔ 左、右导数都存在且相等
(2)有连续一阶导数
⇔
{
①处处可导
②
f
′
(
x
)
连续
\Leftrightarrow \left\{\begin{aligned} ①处处可导 \\ ②f'(x)连续 \end{aligned}\right.
⇔{①处处可导②f′(x)连续
(3)
f
(
x
)
f(x)
f(x)
n
n
n阶可导,最多出现
f
(
n
−
1
)
(
x
)
f^{(n-1)}(x)
f(n−1)(x)
例题1:23李林六套卷(一) 2. 连续、极限存在、可导的定义

分析:

答案:D
例题2:18年1.

分析:
带绝对值的函数,分段(x>0,x<0)求f(x)、f’(x):
推导可知,A、C 有没有绝对值,f(x)表达式都相同,且f’(x)没有分母,一定可导
B.分段求f(x),f’(x),得
f
+
′
(
0
)
=
0
f_+'(0)=0
f+′(0)=0,
f
−
′
(
0
)
=
0
f_-'(0)=0
f−′(0)=0,则
f
′
(
0
)
=
0
f'(0)=0
f′(0)=0,f(x)在x=0处可导
D.分段求f(x),f’(x),得
f
+
′
(
0
)
=
−
1
2
f_+'(0)=-\dfrac{1}{2}
f+′(0)=−21,
f
−
′
(
0
)
=
1
2
f_-'(0)=\dfrac{1}{2}
f−′(0)=21,f(x)在x=0处不可导
答案:D
(4)可导三要素
lim f ( φ ( h ) ) Ψ ( h ) \lim \dfrac{f(φ(h))}{Ψ(h)} limΨ(h)f(φ(h))存在 【高数辅导讲义P54】
①双侧趋近: φ(h)既能趋近0+,又能趋近 0-
②同阶无穷小:φ(h)与Ψ(h)要同阶,或分子更高阶
③一动一定(固定一点)
例题1:高数辅导讲义 P53页例题2 (数一真题)

分析:
A.单侧趋近
B.正确
C.分母比分子高阶,极限不一定存在
D.两动点,没有固定一点
答案:B
例题2:

分析:
A、B:单侧趋近
C.没有固定一点,拆开两个极限不一定单独存在,所以不可拆。必须固定一点。
答案:D
例题3:20年2.

分析:
A、B:题干只说f(x)在(-1,1)内有定义,没说连续,故不可导。取可去间断点的分段函数为反例。A、B❌
C: f(x)在x=0处可导 ⇦⇨
f
′
(
0
)
=
lim
x
→
0
f
(
x
)
−
f
(
0
)
x
−
0
=
lim
x
→
0
f
(
x
)
x
f'(0)=\lim\limits_{x→0}\dfrac{f(x)-f(0)}{x-0}=\lim\limits_{x→0}\dfrac{f(x)}{x}
f′(0)=x→0limx−0f(x)−f(0)=x→0limxf(x)存在 ∴f(x)为x的同阶或高阶无穷小
又因为
∣
x
∣
\sqrt{|x|}
∣x∣比x低阶 ∴
lim
x
→
0
f
(
x
)
∣
x
∣
=
0
\lim\limits_{x→0}\dfrac{f(x)}{\sqrt{|x|}}=0
x→0lim∣x∣f(x)=0。 C✔
D:当f(x)比x²低阶, f ( x ) x 2 \dfrac{f(x)}{x²} x2f(x)应该为∞,不为0;当f(x)与x²同阶, f ( x ) x 2 \dfrac{f(x)}{x²} x2f(x)应该为 k ≠ 0 k≠0 k=0;举反例,取f(x)=x。D❌
答案:C
(5)用导数定义判断可导性
1.含绝对值的导数:
①设
f
(
x
)
=
φ
(
a
)
∣
x
−
a
∣
f(x)=φ(a)|x-a|
f(x)=φ(a)∣x−a∣,且
φ
(
x
)
φ(x)
φ(x)在
x
=
a
x=a
x=a处连续,则
f
(
x
)
f(x)
f(x) 在
x
=
a
x=a
x=a 处可导的充分必要条件是
φ
(
a
)
=
0
φ(a)=0
φ(a)=0
②
∣
x
∣
x
n
|x|x^n
∣x∣xn 在x=0处n阶可导 【
∣
x
∣
|x|
∣x∣在x=0处不可导,
x
∣
x
∣
x|x|
x∣x∣在x=0处1阶可导】
2.带极限号的函数的可导性:
①第一步:求极限,确定f(x)表达式
②第二步,根据f(x)表达式确定可导性
3.几何方法(选填):
画图,左右切线的斜率代表左右导数。若不同,则该点处不可导。
例题1:660 T151
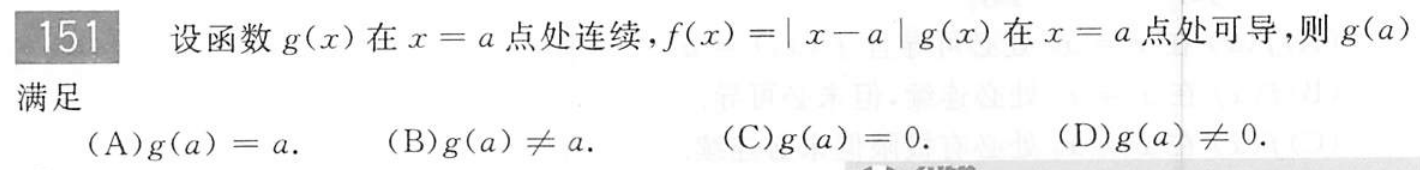
分析:

答案:C
例题2:660 T152

分析:
法一:二级结论:
∣
x
∣
x
n
|x|x^n
∣x∣xn 在x=0处n阶可导
法二:导数定义
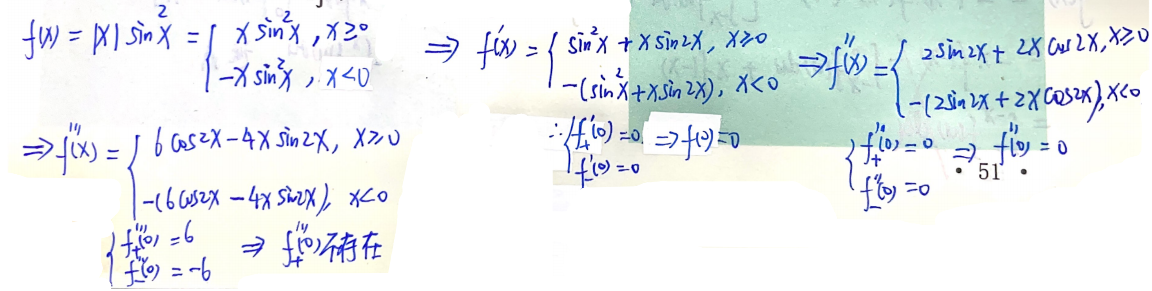
答案:C
例题3:05年7. 带极限号的函数的可导性的判定

分析:带极限号的函数的可导性,第一步:求极限,确定f(x)表达式; 第二步,根据f(x)表达式确定可导性
几何法:
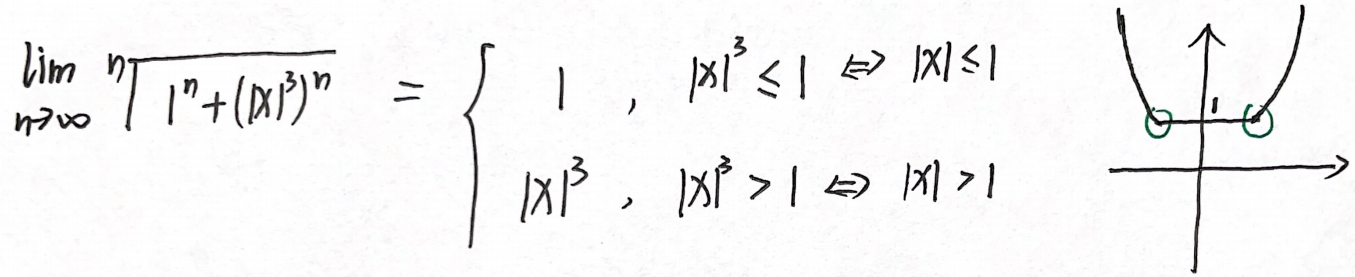
答案:C
2.微分的概念
(1)微分的定义
若 Δ y = f ( x 0 + Δ x ) − f ( x 0 ) Δy=f(x_0+Δx)-f(x_0) Δy=f(x0+Δx)−f(x0) 可以表示为 Δ y = A Δ x + o ( Δ x ) ( Δ x → 0 ) Δy=AΔx+o(Δx) \quad (Δx→0) Δy=AΔx+o(Δx)(Δx→0),则称函数 f ( x ) f(x) f(x)在点 x 0 x_0 x0处可微,称 A Δ x AΔx AΔx为函数 f ( x ) f(x) f(x)在点 x 0 x_0 x0处相应于自变量增量 Δ x Δx Δx的微分,记为 d y = A Δ x dy=AΔx dy=AΔx
微分是函数在这一点 改变量/变化量(增量) 的近似值,是函数改变量的线性主部 (忽略o(Δx))。
(2)微分与可导的关系
函数 y = f ( x ) y=f(x) y=f(x)在点 x 0 x_0 x0处可微的充分必要条件是 f ( x ) f(x) f(x)点 x 0 x_0 x0处可导,且有 d y = f ′ ( x 0 ) Δ x = f ′ ( x 0 ) d x dy=f'(x_0)Δx=f'(x_0){\rm d}x dy=f′(x0)Δx=f′(x0)dx
3.导数与微分的几何意义
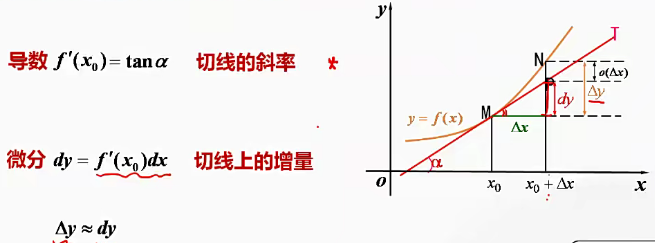
(1)导数 f ′ ( x 0 ) f'(x_0) f′(x0)的几何意义:切线的斜率、相关变化率
平面曲线可以用3种方法表示:①直角坐标 ②参数方程 ③极坐标:根据 { x = ρ c o s θ y = ρ s i n θ \left\{\begin{aligned} x & = ρcosθ \\ y & = ρsinθ \end{aligned}\right. {xy=ρcosθ=ρsinθ 把x、y表示成θ的参数方程
①切线的斜率: f ′ ( x 0 ) = d y d x = tan α = k 切线 f'(x_0)=\dfrac{dy}{dx}=\tanα=k_{切线} f′(x0)=dxdy=tanα=k切线
②法线的斜率 = − 1 切线斜率 -\dfrac{1}{切线斜率} −切线斜率1
③相切 ⇔ { Ⅰ . 函数值相等 Ⅱ . 导数值相等 \Leftrightarrow \left\{\begin{aligned} Ⅰ.函数值相等 \\ Ⅱ.导数值相等 \end{aligned}\right. ⇔{Ⅰ.函数值相等Ⅱ.导数值相等
④相关变化率:
知道一个变化率,求另一个相关的变量的变化率:和求参数方程的导数类似

例题1: ③极坐标

(2)微分的几何意义:切线的增量
①微分
d
y
=
f
′
(
x
0
)
d
x
dy=f'(x_0)dx
dy=f′(x0)dx在几何上表示曲线
y
=
f
(
x
)
y=f(x)
y=f(x)的切线上的增量。
②
Δ
y
=
f
(
x
0
+
Δ
x
)
−
f
(
x
0
)
Δy=f(x_0+Δx)-f(x_0)
Δy=f(x0+Δx)−f(x0)在几何上表示曲线
y
=
f
(
x
)
y=f(x)
y=f(x) 上的增量。
Δ
y
≈
d
y
Δy≈dy
Δy≈dy。
Δx:自变量的增量
Δy:函数的增量,曲线y(x)的增量
dy:函数的微分,切线的增量

例题1:06年7. 微分的几何意义

分析:
法1:画图法
Δ
x
Δx
Δx是自变量的增量,
Δ
y
Δy
Δy是函数曲线的增量,
d
y
dy
dy是切线的增量。在
f
′
(
x
)
>
0
f'(x)>0
f′(x)>0且
f
′
′
(
x
)
>
0
f''(x)>0
f′′(x)>0 的情况下,画图明显可知:0<切线的增量<曲线的增量,即 0<dy<Δy。
法2:拉格朗日中值定理
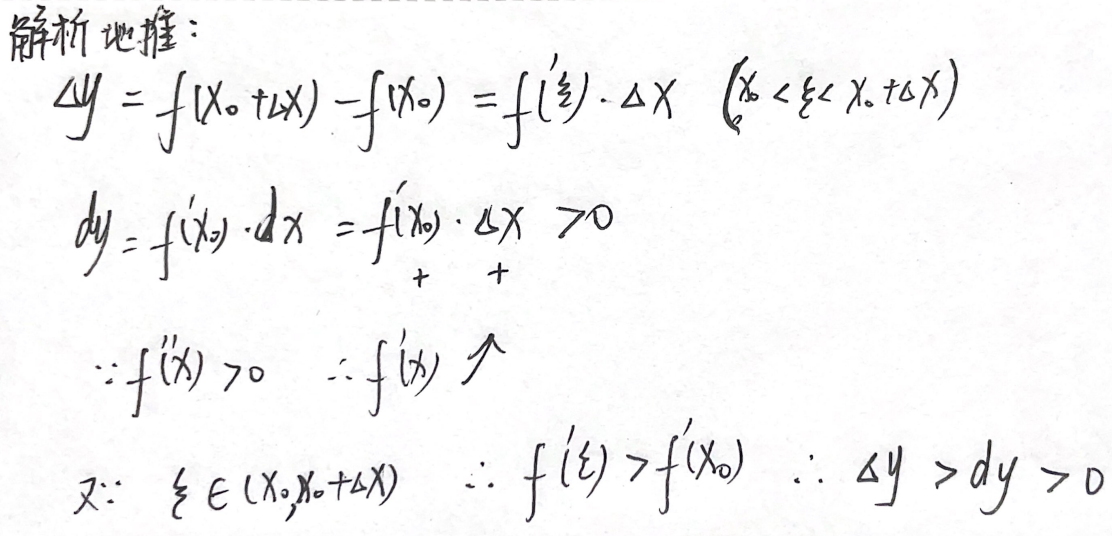
答案:A
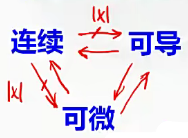
4.连续、可导、可微之间的关系
5.导数公式

(5) ( log a x ) ′ = 1 x ln a (\log_ax)'=\dfrac{1}{x\ln a} (logax)′=xlna1
(6) ( ln ∣ x ∣ ) ′ = 1 x (\ln|x|)'=\dfrac{1}{x} (ln∣x∣)′=x1
(9) ( tan x ) ′ = sec 2 x (\tan x)'=\sec ^2x (tanx)′=sec2x
(11) ( sec x ) ′ = sec x tan x (\sec x)'=\sec x\tan x (secx)′=secxtanx
(14) ( arccos x ) ′ = − 1 1 − x 2 (\arccos x)'=-\dfrac{1}{\sqrt{1-x^2}} (arccosx)′=−1−x21
6.求导法则
(0)结论:奇偶性、周期性、分段函数分段点
1.奇偶函数可导的性质
①f是奇函数,则
f
′
f'
f′为偶函数;f是偶函数,则
f
′
f'
f′为奇函数 【奇函数的导数为偶函数,偶函数的导数为奇函数】
②奇函数在x=0点处的偶次阶导数均为0,即:
f
(
x
)
f(x)
f(x)为奇函数
⇔
\Leftrightarrow
⇔
f
(
2
n
)
(
0
)
=
0
f^{(2n)}(0)=0
f(2n)(0)=0
偶函数在x=0点处的奇次阶导数均为0,即:
f
(
x
)
f(x)
f(x)为偶函数
⇔
\Leftrightarrow
⇔
f
(
2
n
+
1
)
(
0
)
=
0
f^{(2n+1)}(0)=0
f(2n+1)(0)=0
2.周期函数可导的性质:
若
f
(
x
)
f(x)
f(x)是可导的以T为周期的周期函数,则
f
′
(
x
)
f'(x)
f′(x)也是以T为周期的周期函数
3.分段函数在分段点的导数:用导数定义
例题1:17年9.
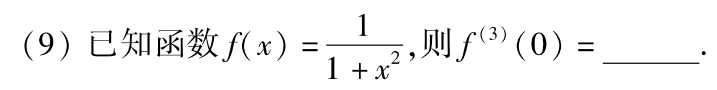
分析:奇偶性
f(x)是偶函数,则
f
′
′
′
(
x
)
f'''(x)
f′′′(x)为奇函数,则
f
′
′
′
(
0
)
=
0
f'''(0)=0
f′′′(0)=0
答案:0
例题2:
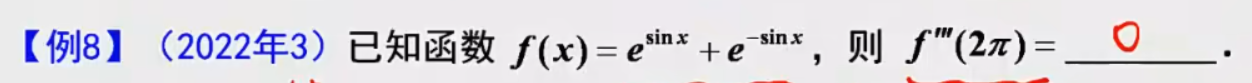
答案:周期性+奇偶性
①周期性:f(x)是可导的以2π为周期的周期函数,则
f
′
′
′
(
x
)
f'''(x)
f′′′(x)也是以2π为周期的周期函数,则
f
′
′
′
(
2
π
)
=
f
′
′
′
(
0
)
f'''(2π)=f'''(0)
f′′′(2π)=f′′′(0)。
②奇偶性:可验证,
f
(
x
)
f(x)
f(x)为偶函数,则
f
′
′
′
(
x
)
f'''(x)
f′′′(x)为奇函数。由奇函数的性质,可得
f
′
′
′
(
0
)
=
0
f'''(0)=0
f′′′(0)=0
(1)有理运算法则
①和、差的导数:
②乘法导数:
③除法导数:
(2)复合函数:链式求导法则 (链导法)
设
u
=
g
(
x
)
u=g(x)
u=g(x)在
x
x
x处可导,
y
=
f
(
u
)
y=f(u)
y=f(u)在相应点处可导【
g
′
(
x
0
)
g'(x_0)
g′(x0)存在,
f
′
[
g
(
x
0
)
]
f'[g(x_0)]
f′[g(x0)]存在】,则复合函数
y
=
f
(
g
(
x
)
)
y=f(g(x))
y=f(g(x))在
x
x
x处可导,且
d
y
d
x
=
d
y
d
u
⋅
d
u
d
x
=
f
′
(
u
)
g
′
(
x
)
\dfrac{dy}{dx}=\dfrac{dy}{du}·\dfrac{du}{dx}=f'(u)g'(x)
dxdy=dudy⋅dxdu=f′(u)g′(x)
由(1)、(2)可解决初等函数的导数 (和差积商、复合)
例题1:23李林四(三)11.
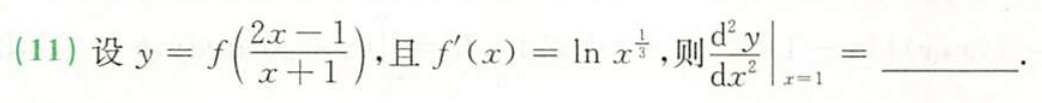
分析:
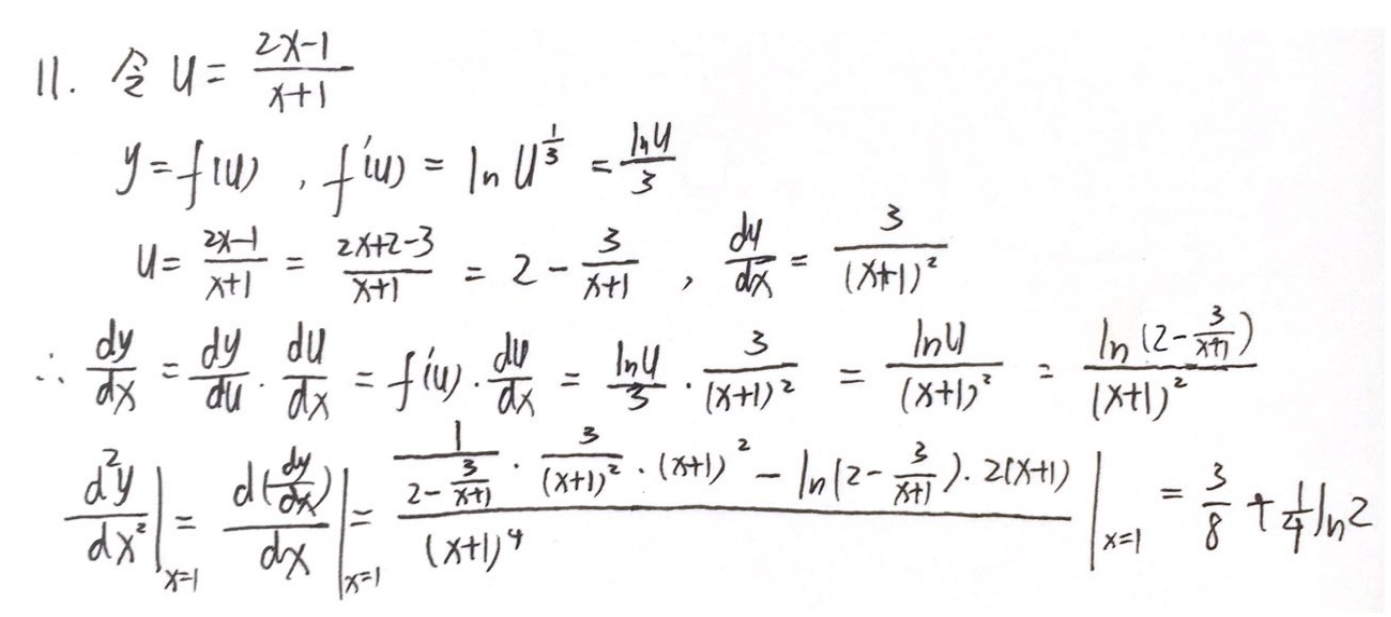
答案:
3
8
+
1
4
ln
2
\dfrac{3}{8}+\dfrac{1}{4}\ln2
83+41ln2
(3)隐函数求导法
求 y ′ ′ ( 0 ) y''(0) y′′(0):
①令x=0,得y(0)
②两边求导,代入x=0、y(0),得 y ′ ( 0 ) y'(0) y′(0)
③再两边求导,代入x=0、y(0)、 y ′ ( 0 ) y'(0) y′(0),得 y ′ ′ ( 0 ) y''(0) y′′(0)
1.概念:
y
=
y
(
x
)
y=y(x)
y=y(x)是由方程
F
(
x
,
y
)
=
0
F(x,y)=0
F(x,y)=0 确定,无法明确求出
y
=
y
(
x
)
y=y(x)
y=y(x)的具体表达式,称
y
(
x
)
y(x)
y(x)为隐函数。
2.方法:
①等式两边求导:隐函数求导:直接两边求导后,直接代入。不必化简为y’ = 多少
②隐函数求导公式:
d
y
d
x
=
−
F
x
′
F
y
′
\dfrac{dy}{dx}=-\dfrac{F'_x}{F'_y}
dxdy=−Fy′Fx′
(4)参数方程求导法
一阶:
d
y
d
x
=
d
y
d
t
d
x
d
t
\dfrac{dy}{dx}=\dfrac{\dfrac{dy}{dt}}{\dfrac{dx}{dt}}
dxdy=dtdxdtdy
二阶:
d
2
y
d
x
2
=
d
(
d
y
d
x
)
d
x
=
d
(
d
y
d
x
)
d
t
d
x
d
t
=
y
′
′
(
t
)
x
′
(
t
)
−
x
′
′
(
t
)
y
′
(
t
)
x
′
3
(
t
)
\dfrac{d^2y}{dx^2}=\dfrac{d(\dfrac{dy}{dx})}{dx}=\dfrac{\dfrac{d(\dfrac{dy}{dx})}{dt}}{\dfrac{dx}{dt}}=\dfrac{y''(t)x'(t)-x''(t)y'(t)}{x'^3(t)}
dx2d2y=dxd(dxdy)=dtdxdtd(dxdy)=x′3(t)y′′(t)x′(t)−x′′(t)y′(t)

例题1:10年9.
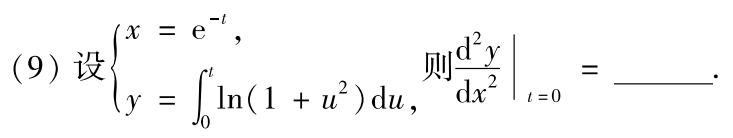
分析:
法一:链式求导
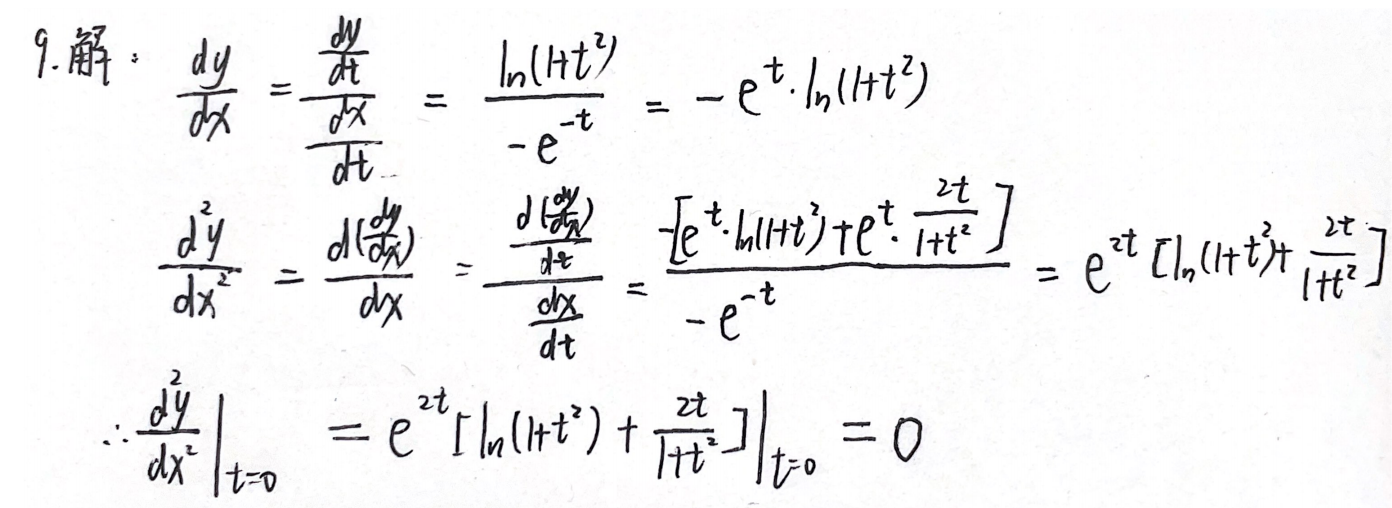
法二:公式法: d 2 y d x 2 = y ′ ′ ( t ) x ′ ( t ) − x ′ ′ ( t ) y ′ ( t ) x ′ 3 ( t ) \dfrac{d^2y}{dx^2}=\dfrac{y''(t)x'(t)-x''(t)y'(t)}{x'^3(t)} dx2d2y=x′3(t)y′′(t)x′(t)−x′′(t)y′(t)
答案:0
例题2:23李林六套卷(六)12. 参数方程 + 导数定义
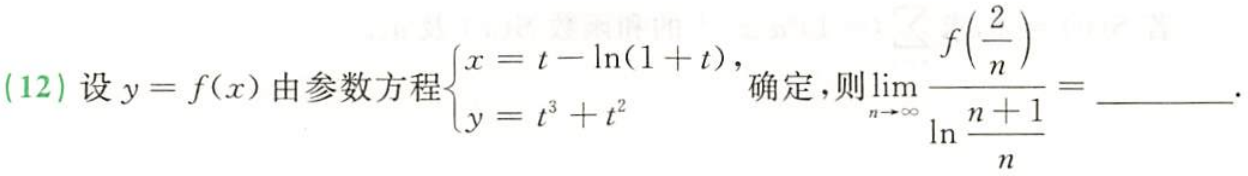
分析:
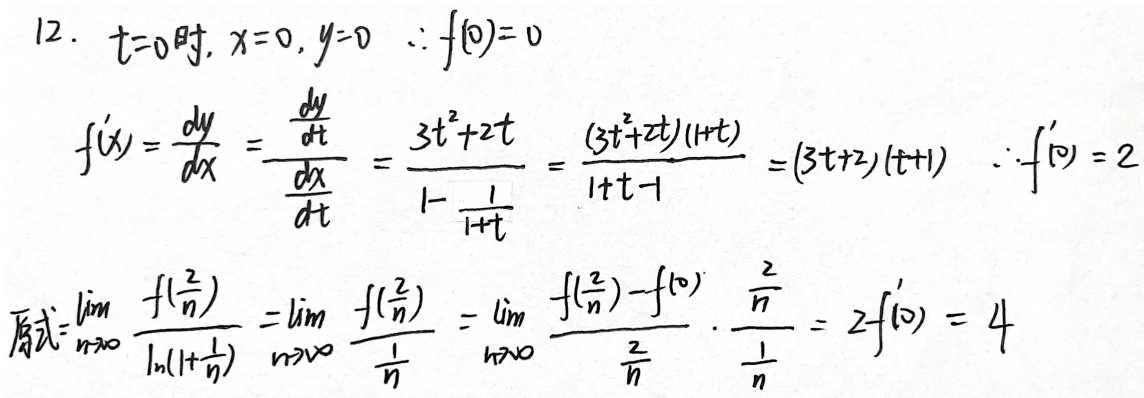
答案:4
(5)反函数的导数
一阶反函数的导数: φ ′ ( y ) = 1 f ′ ( x ) φ'(y)=\dfrac{1}{f'(x)} φ′(y)=f′(x)1
二阶反函数的导数: φ ′ ′ ( y ) = − f ′ ′ ( x ) f ′ 3 ( x ) φ''(y)=-\dfrac{f''(x)}{f'^3(x)} φ′′(y)=−f′3(x)f′′(x) 【注意:求φ’'(1),是y=1,此时x等于多少还需要代入原式求x的值】
推导:
① d x d y = 1 d y d x = 1 y ′ \dfrac{dx}{dy}=\dfrac{1}{\dfrac{dy}{dx}}=\dfrac{1}{y'} dydx=dxdy1=y′1
② d 2 x d y 2 = d ( d x d y ) d y = d ( d x d y ) d x d x d y = − y ′ ′ ( y ′ ) 2 1 y ′ = − y ′ ′ ( y ′ ) 3 \dfrac{d^2x}{dy^2}=\dfrac{d(\dfrac{dx}{dy})}{dy}=\dfrac{d(\dfrac{dx}{dy})}{dx}\dfrac{dx}{dy}=-\dfrac{y''}{(y')^2}\dfrac{1}{y'}=-\dfrac{y''}{(y')^3} dy2d2x=dyd(dydx)=dxd(dydx)dydx=−(y′)2y′′y′1=−(y′)3y′′

(6)对数求导法
由于和差的导数比乘除的导数运算简单,因此取对数,利用对数的运算法则,可将乘除的导数变为和差的导数。例如表达式:多个因式的乘除、乘幂、幂指函数的形式【连乘、连除、乘方、开方】
(7)高阶导数
(1)4个常用的高阶导数公式:
①
(
sin
x
)
(
n
)
=
sin
(
x
+
n
π
2
)
(\sin x)^{(n)}=\sin(x+\dfrac{nπ}{2})
(sinx)(n)=sin(x+2nπ)
② ( cos x ) ( n ) = cos ( x + n π 2 ) (\cos x)^{(n)}=\cos(x+\dfrac{nπ}{2}) (cosx)(n)=cos(x+2nπ)
③ ( u ± v ) ( n ) = u ( n ) ± v ( n ) (u±v)^{(n)}=u^{(n)}±v^{(n)} (u±v)(n)=u(n)±v(n)
④ ( u v ) ( n ) = ∑ k = 0 n C n k u ( k ) v ( n − k ) (uv)^{(n)}=\sum\limits_{k=0}^n{\rm C}_n^ku^{(k)}v^{(n-k)} (uv)(n)=k=0∑nCnku(k)v(n−k) 【乘法的n阶导数公式:莱布尼茨公式】
1 1 + x 、 ln ( 1 + x ) \dfrac{1}{1+x}、\ln(1+x) 1+x1、ln(1+x)的n阶导数,没必要背,求1阶、2阶,归纳n阶导数规律 即可
(2)求1阶,2阶导数,归纳n阶导数的规律
例如: ( 1 x + a ) ( n ) = ( − 1 ) n n ! ( x + a ) n + 1 (\dfrac{1}{x+a})^{(n)}=(-1)^n\dfrac{n!}{(x+a)^{n+1}} (x+a1)(n)=(−1)n(x+a)n+1n!,这种公式没必要背,现推很快的。
(3)泰勒公式:
f
(
n
)
(
x
0
)
=
a
n
⋅
n
!
f^{(n)}(x_0)=a_n·n!
f(n)(x0)=an⋅n!
f
(
x
)
=
a
0
+
a
1
(
x
−
x
0
)
+
a
2
(
x
−
x
0
)
2
+
a
3
(
x
−
x
0
)
3
+
.
.
.
+
a
n
(
x
−
x
0
)
n
+
o
(
(
x
−
x
0
)
n
)
(
x
→
x
0
)
f(x)=a₀+a₁(x-x₀)+a₂(x-x₀)²+a₃(x-x₀)³+...+a_n(x-x₀)^n+o((x-x₀)^n) (x→x₀)
f(x)=a0+a1(x−x0)+a2(x−x0)2+a3(x−x0)3+...+an(x−x0)n+o((x−x0)n)(x→x0)
总结:
(1)n阶导数公式、(2)求1阶2阶导数归纳规律:用于求n阶导函数 f ( n ) ( x ) f^{(n)}(x) f(n)(x)
(3)泰勒公式:用于求具体点 x 0 x_0 x0的n阶导数 f ( n ) ( x 0 ) f^{(n)}(x_0) f(n)(x0)
例题1:16年12. 泰勒公式
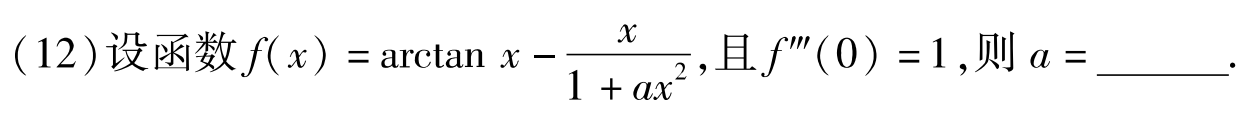
分析:
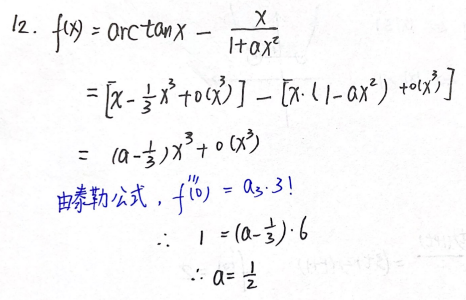
答案:
1
2
\dfrac{1}{2}
21
例题2:

分析:
法一:求一阶、二阶、三阶导数,归纳规律
法二:泰勒公式
f
(
n
)
(
0
)
=
a
n
⋅
n
!
f^{(n)}(0)=a_n·n!
f(n)(0)=an⋅n!

答案:
(
−
1
)
n
⋅
2
n
⋅
n
!
3
n
+
1
\dfrac{(-1)^n·2^n·n!}{3^{n+1}}
3n+1(−1)n⋅2n⋅n!
例题3:880 多元 综合填空3

例题4:武钟祥每日一题 24-Day60 啊,我“拆”开了!

分析:

二、微分中值定理与导数应用

1.微分中值定理
(0)费马引理

(1)罗尔定理
罗尔定理:如果函数f(x)满足:
(1)在闭区间
[
a
,
b
]
[a,b]
[a,b] 上连续
(2)在开区间
(
a
,
b
)
(a,b)
(a,b) 内可导
(3)在区间端点处的函数值相等,即
f
(
a
)
=
f
(
b
)
f(a)=f(b)
f(a)=f(b)
那么在开区间
(
a
,
b
)
(a,b)
(a,b) 内至少有一点
ξ
(
a
<
ξ
<
b
)
ξ (a<ξ<b)
ξ(a<ξ<b),使得
f
′
(
ξ
)
=
0
f'(ξ)=0
f′(ξ)=0 :
∃
ξ
∈
(
a
,
b
)
,使
f
′
(
ξ
)
=
0
\existξ∈(a,b),使 f'(ξ)=0
∃ξ∈(a,b),使f′(ξ)=0

(2)拉格朗日中值定理
若函数f(x)满足:
(1)在闭区间
[
a
,
b
]
[a,b]
[a,b] 上连续
(2)在开区间
(
a
,
b
)
(a,b)
(a,b) 内可导
那么在开区间
(
a
,
b
)
(a,b)
(a,b) 内至少有一点ξ (a<ξ<b),使如下等式成立:ョξ∈(a,b),使得
f
(
b
)
−
f
(
a
)
=
f
′
(
ξ
)
(
b
−
a
)
(
a
<
ξ
<
b
)
或
f
′
(
ξ
)
=
f
(
b
)
−
f
(
a
)
b
−
a
(
a
<
ξ
<
b
)
f(b)-f(a)=f'(ξ)(b-a)\qquad (a<ξ<b)\\[5mm] 或 \qquad f'(ξ)=\dfrac{f(b)-f(a)}{b-a}\qquad (a<ξ<b)
f(b)−f(a)=f′(ξ)(b−a)(a<ξ<b)或f′(ξ)=b−af(b)−f(a)(a<ξ<b)


1.罗尔定理与拉格朗日中值定理的关系:
①罗尔定理是拉格朗日中值定理的特例:f(a)=f(b),则f’(ξ)=0
②拉格朗日中值定理是罗尔定理的推广
2.拉朗转化功能
①
f
(
b
)
−
f
(
a
)
b
−
a
\dfrac{f(b)-f(a)}{b-a}
b−af(b)−f(a)不会操作,转化为
f
′
(
ξ
)
f'(ξ)
f′(ξ)
②
f
(
b
)
−
f
(
a
)
f(b)-f(a)
f(b)−f(a)不好操作,转化为
(
b
−
a
)
f
′
(
ξ
)
(b-a)f'(ξ)
(b−a)f′(ξ)
③
f
′
(
b
)
−
f
′
(
a
)
f'(b)-f'(a)
f′(b)−f′(a)不好操作,转化为
(
b
−
a
)
f
′
′
(
ξ
)
(b-a)f''(ξ)
(b−a)f′′(ξ)
3.证明拉格朗日中值定理:构造辅助函数,用罗尔定理

(3)柯西中值定理

证明:①是传统的辅助函数,但难于验证F(a)=F(b) ②是更好的辅助函数,更易得F(a)=F(b)

(4)泰勒中值定理 (泰勒公式拉格朗日余项)

佩阿诺余项:局部性态,研究极限
拉格朗日余弦:整体性态,研究中值定理
总结
1.四大中值定理的本质
①罗尔、拉朗、柯西 三者建立了函数值与一阶导数的联系
f
(
x
)
⇦⇨
f
′
(
x
)
f(x)⇦⇨f'(x)
f(x)⇦⇨f′(x)。给函数,证导数 / 给导数,证函数。
②泰勒中值定理:函数值
f
(
x
)
f(x)
f(x)与高阶导数
f
(
n
)
(
x
)
f^{(n)}(x)
f(n)(x)
2.四者的关系:
罗尔定理
⇌
推广
特例
拉格朗日中值定理
⇌
推广
特例
柯西中值定理
罗尔定理 \underset{特例}{\xrightleftharpoons{推广}} 拉格朗日中值定理\underset{特例}{\xrightleftharpoons{推广}}柯西中值定理
罗尔定理特例推广
拉格朗日中值定理特例推广
柯西中值定理
但是,拉朗和柯西都是通过 罗尔定理+构造辅助函数 证明出来的

微分中值定理的证明题
(1)单中值:证明存在一个点ξ∈(a,b),使 g [ ξ , f ( ξ ) , f ′ ( ξ ) ] = 0 g[ξ,f(ξ),f'(ξ)]=0 g[ξ,f(ξ),f′(ξ)]=0
方法:构造辅助函数,用罗尔定理:
构造辅助函数的三种方法:
1.分析法(还原法)
观察分析,确定辅助函数F(x),使得
F
′
(
x
)
=
g
[
ξ
,
f
(
ξ
)
,
f
′
(
ξ
)
]
F'(x)=g[ξ,f(ξ),f'(ξ)]
F′(x)=g[ξ,f(ξ),f′(ξ)]。且F(x)有两个端点函数值相等,用罗尔定理可得
F
′
(
x
)
=
g
[
ξ
,
f
(
ξ
)
,
f
′
(
ξ
)
]
=
0
F'(x)=g[ξ,f(ξ),f'(ξ)]=0
F′(x)=g[ξ,f(ξ),f′(ξ)]=0。
2.微分方程法
①求微分方程
g
[
x
,
y
,
y
′
]
=
0
g[x,y,y']=0
g[x,y,y′]=0的通解
H
(
x
,
y
)
=
C
H(x,y)=C
H(x,y)=C
②设辅助函数:
F
(
x
)
=
H
(
x
,
f
(
x
)
)
F(x)=H(x,f(x))
F(x)=H(x,f(x))
3.常用辅助函数:【辅导讲义P79】
①
ξ
f
′
(
ξ
)
+
n
f
(
ξ
)
=
0
ξf'(ξ)+nf(ξ)=0
ξf′(ξ)+nf(ξ)=0,令
F
(
x
)
=
x
n
f
(
x
)
F(x)=x^nf(x)
F(x)=xnf(x)
② ξ f ′ ( ξ ) − n f ( ξ ) = 0 ξf'(ξ)-nf(ξ)=0 ξf′(ξ)−nf(ξ)=0,令 F ( x ) = f ( x ) x n F(x)=\dfrac{f(x)}{x^n} F(x)=xnf(x)
③ f ′ ( ξ ) + λ f ( ξ ) = 0 f'(ξ)+λf(ξ)=0 f′(ξ)+λf(ξ)=0,令 F ( x ) = e λ x f ( x ) F(x)=e^{λx}f(x) F(x)=eλxf(x)
④ f ′ ( ξ ) + g ( ξ ) f ( ξ ) = 0 f'(ξ)+g(ξ)f(ξ)=0 f′(ξ)+g(ξ)f(ξ)=0,令 F ( x ) = e ∫ g ( x ) d x f ( x ) F(x)=e^{\int g(x)dx}f(x) F(x)=e∫g(x)dxf(x)
(2)双中值:证明存在两个中值点 ξ,η∈(a,b),使 g [ ξ , η , f ( ξ ) , f ( η ) , f ′ ( ξ ) , f ′ ( η ) ] = 0 g[ξ,η,f(ξ),f(η),f'(ξ),f'(η)]=0 g[ξ,η,f(ξ),f(η),f′(ξ),f′(η)]=0
1.方法:
(1)不要求
ξ
≠
η
ξ≠η
ξ=η
在同一区间[a,b]上用两次中值定理(拉格朗日、柯西中值定理)
(2)要求
ξ
≠
η
ξ≠η
ξ=η
将区间[a,b]分为两个子区间,在两个子区间上分别用拉格朗日中值定理
难点和关键点:两个子区间上分界点的选取:
①用第一问的结论
②逆推法:先假设一个分界点c,(a,c)和(c,b)上各用一次拉格朗日中值定理,代入要证明的条件,观察
f
(
c
)
f(c)
f(c)的选取。【辅导讲义P83例5】
(3)高阶导数:证明存在一个中值点 ξ∈(a,b),使 g [ ξ , f ( n ) ( ξ ) ] ≥ 0 ( n ≥ 2 ) g[ξ,f^{(n)}(ξ)]≥0 \ (n≥2) g[ξ,f(n)(ξ)]≥0 (n≥2)
方法:用带拉格朗日余项的泰勒公式,展开点 x 0 x_0 x0选提供函数值和导数值信息多的点。(当提供函数值、提供导数值信息一样多,如都各自提供一个,此时选提供导数值的点展开,然后分别令x=提供函数值的点,代入泰勒公式 【辅导讲义P85例题2】)
2.泰勒公式
泰勒公式的伟大意义:
①建立了函数值与高阶导数之间的联系:
f
(
x
)
⇦⇨
f
(
n
)
(
x
)
f(x)⇦⇨f^{(n)}(x)
f(x)⇦⇨f(n)(x) 【题目出现了n阶导数,应该要想到泰勒公式】
②用多项式逼近。多项式求极限、求导数、求积分都比较简单。

(1)泰勒中值定理1:佩亚诺余项,局部泰勒公式,用于极限的计算
f ( x ) = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) + f ′ ′ ( x 0 ) 2 ! ( x − x 0 ) 2 + f ′ ′ ′ ( x 0 ) 3 ! ( x − x 0 ) 3 + . . . + f ( n ) ( x 0 ) n ! ( x − x 0 ) n + o ( ( x − x 0 ) n ) f(x)=f(x_0)+f'(x_0)(x-x_0)+\dfrac{f''(x_0)}{2!}(x-x_0)^2+\dfrac{f'''(x_0)}{3!}(x-x_0)^3+...+\dfrac{f^{(n)}(x_0)}{n!}(x-x_0)^n+o((x-x_0)^n) f(x)=f(x0)+f′(x0)(x−x0)+2!f′′(x0)(x−x0)2+3!f′′′(x0)(x−x0)3+...+n!f(n)(x0)(x−x0)n+o((x−x0)n)
佩亚诺余项(用于计算极限): R n ( x ) = o ( ( x − x 0 ) n ) R_n(x)=o((x-x_0)^n) Rn(x)=o((x−x0)n)
(2)泰勒中值定理2:拉格朗日余项,整体泰勒公式,用于证明
f ( x ) = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) + f ′ ′ ( x 0 ) 2 ! ( x − x 0 ) 2 + f ′ ′ ′ ( x 0 ) 3 ! ( x − x 0 ) 3 + . . . + f ( n ) ( x 0 ) n ! ( x − x 0 ) n + R n ( x ) f(x)=f(x_0)+f'(x_0)(x-x_0)+\dfrac{f''(x_0)}{2!}(x-x_0)^2+\dfrac{f'''(x_0)}{3!}(x-x_0)^3+...+\dfrac{f^{(n)}(x_0)}{n!}(x-x_0)^n+R_n(x) f(x)=f(x0)+f′(x0)(x−x0)+2!f′′(x0)(x−x0)2+3!f′′′(x0)(x−x0)3+...+n!f(n)(x0)(x−x0)n+Rn(x)
拉格朗日余项(用于证明): R n ( x ) = f ( n + 1 ) ( ξ ) ( n + 1 ) ! ( x − x 0 ) n + 1 ( x 0 < ξ < x ) R_n(x)=\dfrac{f^{(n+1)}(ξ)}{(n+1)!}(x-x_0)^{n+1} (x_0<ξ<x) Rn(x)=(n+1)!f(n+1)(ξ)(x−x0)n+1(x0<ξ<x)
(3)麦克劳林公式
| 原式 | 泰勒展开 (写到3阶) |
|---|---|
| e x e^x ex | 1 + x + x 2 2 ! + x 3 3 ! + o ( x 3 ) 1+x+\dfrac{x^2}{2!}+\dfrac{x^3}{3!}+o(x^3) 1+x+2!x2+3!x3+o(x3) |
| sin x \sin x sinx | x − x 3 3 ! + x 5 5 ! + o ( x 5 ) x-\dfrac{x³}{3!}+\dfrac{x^5}{5!}+o(x^5) x−3!x3+5!x5+o(x5) |
| cos x \cos x cosx | 1 − x 2 2 ! + x 4 4 ! + o ( x 4 ) 1-\dfrac{x^2}{2!}+\dfrac{x^4}{4!}+o(x^4) 1−2!x2+4!x4+o(x4) |
| a r c s i n x \rm arcsinx arcsinx | x + x 3 3 ! + o ( x 3 ) x+\dfrac{x^3}{3!}+o(x^3) x+3!x3+o(x3) |
| 1 1 − x \dfrac{1}{1-x} 1−x1 | 1 + x + x 2 + x 3 + o ( x 3 ) 1+x+x^2+x^3+o(x^3) 1+x+x2+x3+o(x3) |
| 1 1 + x \dfrac{1}{1+x} 1+x1 | 1 − x + x 2 − x 3 + o ( x 3 ) 1-x+x^2-x^3+o(x^3) 1−x+x2−x3+o(x3) |
| ln ( 1 + x ) \ln(1+x) ln(1+x) | x − x 2 2 + x 3 3 x-\dfrac{x^2}{2}+\dfrac{x^3}{3} x−2x2+3x3 − x 4 4 + . . . + ( − 1 ) n + 1 x n n + o ( x n ) -\dfrac{x^4}{4}+...+(-1)^{n+1}\dfrac{x^n}{n}+o(x^n) −4x4+...+(−1)n+1nxn+o(xn) |
| 1 1 + x 2 \dfrac{1}{1+x^2} 1+x21 | 1 − x 2 + x 4 − x 6 + . . . 1-x^2+x^4-x^6+... 1−x2+x4−x6+... |
| a r c t a n x {\rm arctan}x arctanx | x − x 3 3 + x 5 5 + . . . x-\dfrac{x^3}{3}+\dfrac{x^5}{5}+... x−3x3+5x5+... |
| t a n x {\rm tan}x tanx | x + x 3 3 + o ( x 3 ) x+\dfrac{x³}{3}+o(x³) x+3x3+o(x3) |
| ( 1 + x ) α (1+x)^α (1+x)α | 1 + α x + α ( α − 1 ) 2 ! x 2 + . . . + α ( α − 1 ) . . . ( α − n + 1 ) n ! x n + o ( x n ) 1+αx+\dfrac{α(α-1)}{2!}x^2+...+\dfrac{α(α-1)...(α-n+1)}{n!}x^n+o(x^n) 1+αx+2!α(α−1)x2+...+n!α(α−1)...(α−n+1)xn+o(xn) |
3.单调性与极值、最值
(1)函数的极值
1.极值的定义
设函数f(x)在点
x
0
x_0
x0的某邻域
U
(
x
0
)
U(x_0)
U(x0)内有定义,如果对于去心邻域
U
˚
(
x
0
)
Ů(x_0)
U˚(x0)内的任一x,【极值是局部形态】
恒有
f
(
x
)
<
f
(
x
0
)
f(x)<f(x_0)
f(x)<f(x0),则称
x
0
x_0
x0为
f
(
x
)
f(x)
f(x)的一个极大值点,称
f
(
x
0
)
f(x_0)
f(x0)是函数
f
(
x
)
f(x)
f(x)的一个极大值。
恒有
f
(
x
)
>
f
(
x
0
)
f(x)>f(x_0)
f(x)>f(x0),则称
x
0
x_0
x0为
f
(
x
)
f(x)
f(x)的一个极小值点,称
f
(
x
0
)
f(x_0)
f(x0)是函数
f
(
x
)
f(x)
f(x)的一个极小值。
函数的极大值与极小值统称为函数的极值,使函数取得极值的点称为极值点。
极大值可能小于极小值,没有大小关系

2.极值的判定
(1)极值的必要条件:
y
=
f
(
x
)
y=f(x)
y=f(x),①
x
0
x_0
x0是极值点 + ②
f
(
x
)
f(x)
f(x)在点
x
0
x_0
x0处可导 ⇨
x
0
x_0
x0是驻点,即
f
′
(
x
0
)
=
0
f'(x_0)=0
f′(x0)=0
【意思是:①可导函数f(x)的极值点,一定是它的驻点。②驻点不一定是极值点,如f(x)=x³ ③函数f(x)的极值点,不一定是它的驻点,因为极值点处可能不可导。如f(x)=|x|】
(1)可能的极值点:
①驻点,即 f ′ ( x 0 ) = 0 f'(x_0)=0 f′(x0)=0
②不可导点,即 f ′ ( x 0 ) f'(x_0) f′(x0)不存在
(2)普通函数f(x)的极值点与驻点没有关系
(2)极值的充分条件:
①极值第一充分条件:
x
0
x_0
x0两侧:①
f
′
(
x
)
f'(x)
f′(x)变号 或
f
(
x
)
f(x)
f(x)单调性相反
Ⅰ.极大值:
f
′
(
x
)
f'(x)
f′(x)由正变负 或
f
(
x
)
f(x)
f(x)由单增变单减
Ⅱ.极小值:
f
′
(
x
)
f'(x)
f′(x)由负变正 或
f
(
x
)
f(x)
f(x)由单减变单增
Ⅲ.没有极值:
f
′
(
x
)
f'(x)
f′(x)不变号 或
f
(
x
)
f(x)
f(x)单调性不变
②极值第二充分条件
设函数f(x)在
x
0
x_0
x0处具有二阶导数且
f
′
(
x
0
)
=
0
,
f
′
′
(
x
0
)
≠
0
f'(x_0)=0,f''(x_0)≠0
f′(x0)=0,f′′(x0)=0,则
Ⅰ.当
f
′
(
x
0
)
=
0
,
f
′
′
(
x
0
)
<
0
f'(x_0)=0,f''(x_0)<0
f′(x0)=0,f′′(x0)<0时,函数f(x)在
x
0
x_0
x0处取得极大值
Ⅱ.当
f
′
(
x
0
)
=
0
,
f
′
′
(
x
0
)
>
0
f'(x_0)=0,f''(x_0)>0
f′(x0)=0,f′′(x0)>0时,函数f(x)在
x
0
x_0
x0处取得极小值
③极值第三充分条件
若
y
=
f
(
x
)
y=f(x)
y=f(x)在
x
0
x_0
x0的某邻域内有n阶导数,且
f
′
(
x
0
)
=
f
′
′
(
x
0
)
=
.
.
.
=
f
(
n
−
1
)
(
x
0
)
=
0
f'(x_0)=f''(x_0)=...=f^{(n-1)}(x_0)=0
f′(x0)=f′′(x0)=...=f(n−1)(x0)=0,但
f
(
n
)
(
x
0
)
≠
0
f^{(n)}(x_0)≠0
f(n)(x0)=0,则
(1)n为偶数,则
x
0
x_0
x0为
f
(
x
)
f(x)
f(x)的极值点。且
f
(
n
)
(
x
0
)
>
0
f^{(n)}(x_0)>0
f(n)(x0)>0为极小值,
f
(
n
)
(
x
0
)
<
0
f^{(n)}(x_0)<0
f(n)(x0)<0为极大值
(2)n为奇数,f(x)在
x
0
x_0
x0处无极值,但
(
x
0
,
f
(
x
0
)
)
(x_0,f(x_0))
(x0,f(x0))为曲线y=f(x)的拐点

(2)函数的最大值、最小值
1.求连续函数f(x)在闭区间[a,b]上的最值:
①求出(a,b)内所有驻点和不可导点
②求出驻点函数值、不可导点函数值、端点函数值。
③比较大小,最大的为最大值,最小的最小值
注:若函数f(x)在(a,b)内仅有唯一极值点,则唯一极值点处就取得最值
2.最大最小值应用题:
①建立目标函数
②求最大值最小值
4.曲线的凹凸性与拐点
(1)凹凸性
(1)凹:判定方法:
①定义:
f
(
x
1
+
x
2
2
)
<
f
(
x
1
)
+
f
(
x
2
)
2
f(\dfrac{x_1+x_2}{2})<\dfrac{f(x_1)+f(x_2)}{2}
f(2x1+x2)<2f(x1)+f(x2)
②二阶导:
f
′
′
(
x
)
>
0
f''(x)>0
f′′(x)>0
③曲线形状: 曲线是凹的
(2)凸:判定方法:
①定义:
f
(
x
1
+
x
2
2
)
>
f
(
x
1
)
+
f
(
x
2
)
2
f(\dfrac{x_1+x_2}{2})>\dfrac{f(x_1)+f(x_2)}{2}
f(2x1+x2)>2f(x1)+f(x2)
②二阶导:
f
′
′
(
x
)
<
0
f''(x)<0
f′′(x)<0
③曲线形状: 曲线是凸的

(2)拐点

1.拐点的定义:
(
x
0
,
f
(
x
0
)
)
(x_0,f(x_0))
(x0,f(x0))是曲线上的点,一对坐标。
拐点
x
0
x_0
x0两侧凹凸性改变:凹→凸、凸→凹
2.拐点的判定:(一个必要,三个充分)
(1)拐点的必要条件:
f
′
′
(
x
0
)
=
0
f''(x_0)=0
f′′(x0)=0 或
f
′
′
(
x
0
)
f''(x_0)
f′′(x0)不存在
(2)拐点的充分条件:
①拐点的第一充分条件:
x
0
x_0
x0左右两侧
f
′
′
(
x
)
f''(x)
f′′(x) 异号 或
f
′
(
x
)
f'(x)
f′(x) 在
x
0
x_0
x0两侧单调性相反
②拐点的第二充分条件:
f
′
′
(
x
0
)
=
0
,
f
′
′
′
(
x
0
)
≠
0
f''(x_0)=0,f'''(x_0)≠0
f′′(x0)=0,f′′′(x0)=0
③拐点的第三充分条件:若
f
′
′
(
x
0
)
=
f
′
′
′
(
x
0
)
=
.
.
.
=
f
(
n
−
1
)
(
x
0
)
=
0
f''(x_0)=f'''(x_0)=...=f^{(n-1)}(x_0)=0
f′′(x0)=f′′′(x0)=...=f(n−1)(x0)=0,但
f
(
n
)
(
x
0
)
≠
0
f^{(n)}(x_0)≠0
f(n)(x0)=0,n为奇数【最高次导数为奇数阶导数不为0,为拐点】【2到n-1阶导为0,不要求1阶导为0】
奇数阶导数不为0:拐点 ;举例: f ′ ( x 0 ) = f ′ ′ ( x 0 ) = f ′ ′ ′ ( x 0 ) = f ( 4 ) ( x 0 ) = 0 , f ( 5 ) ( x 0 ) ≠ 0 f'(x_0)=f''(x_0)=f'''(x_0)=f^{(4)}(x_0)=0,f^{(5)}(x_0)≠0 f′(x0)=f′′(x0)=f′′′(x0)=f(4)(x0)=0,f(5)(x0)=0,则 x 0 x_0 x0为拐点
偶数阶导数不为0:极值点 ;举例: f ′ ( x 0 ) = f ′ ′ ( x 0 ) = f ′ ′ ′ ( x 0 ) = 0 , f ( 4 ) ( x 0 ) ≠ 0 f'(x_0)=f''(x_0)=f'''(x_0)=0,f^{(4)}(x_0)≠0 f′(x0)=f′′(x0)=f′′′(x0)=0,f(4)(x0)=0,则 x 0 x_0 x0为极值点
3.极值点 vs 拐点:
(1)极值点是x轴上的点
x
=
x
0
x=x_0
x=x0,拐点是曲线上的点
(
x
0
,
y
0
)
(x_0,y_0)
(x0,y0)
(2)点的必要条件、第一第二充分条件,就是极值的必要条件、第一第二充分条件抬高一阶
(3)①可导函数的可导的点,不能同时出现极值点和拐点:
x
0
x_0
x0若为极值点,则
(
x
0
,
f
(
x
0
)
)
(x_0,f(x_0))
(x0,f(x0))不会是拐点。若
(
x
0
,
f
(
x
0
)
)
(x_0,f(x_0))
(x0,f(x0))为拐点,则
x
0
x_0
x0不会是极值点。
②不可导的点(如分段函数分界点),可以同时出现极值点和拐点
即,
f
(
x
)
f(x)
f(x)在
x
=
x
0
x=x_0
x=x0不可导,
x
=
x
0
x=x_0
x=x0与
(
x
0
,
f
(
x
0
)
)
(x_0,f(x_0))
(x0,f(x0))可以同时是
y
=
f
(
x
)
y=f(x)
y=f(x)的极值点与拐点。 【660 T161】
5.曲线的渐近线
(1)渐近线的本质:割线的极限位置
(2)分析顺序:①铅直渐渐线→ ②水平渐近线(双向)→ ③斜渐近线(双向)
(3)铅直渐近线可以有无数条,而 水平渐近线+斜渐近线 最多只能有2条,为x轴的正向和负向
①水平渐近线 (双向)
水平渐近线有+∞和-∞两个方向
若有
lim
x
→
+
∞
f
(
x
)
=
c
\lim\limits_{x→+∞}f(x)=c
x→+∞limf(x)=c 或者
lim
x
→
−
∞
f
(
x
)
=
c
\lim\limits_{x→-∞}f(x)=c
x→−∞limf(x)=c
则称
y
=
c
y=c
y=c为曲线
y
=
f
(
x
)
y=f(x)
y=f(x)的水平渐近线
②铅直渐近线 (找无穷间断点)
有无穷间断点a,则 x=a 为曲线的铅直渐近线
③斜渐近线 (双向)
斜渐近线也有+∞和-∞两个方向。有该方向上的水平渐近线,则无该方向上的斜渐近线。即,水平渐近线 + 斜渐近线 ≤ 2
若有
lim
x
→
+
∞
f
(
x
)
x
=
a
≠
0
\lim\limits_{x→+∞}\dfrac{f(x)}{x}=a≠0
x→+∞limxf(x)=a=0 且
lim
x
→
+
∞
(
f
(
x
)
−
a
x
)
=
b
\lim\limits_{x→+∞}(f(x)-ax)=b
x→+∞lim(f(x)−ax)=b
或者
lim
x
→
−
∞
f
(
x
)
x
=
a
≠
0
\lim\limits_{x→-∞}\dfrac{f(x)}{x}=a≠0
x→−∞limxf(x)=a=0 且
lim
x
→
−
∞
(
f
(
x
)
−
a
x
)
=
b
\lim\limits_{x→-∞}(f(x)-ax)=b
x→−∞lim(f(x)−ax)=b
则称
y
=
a
x
+
b
y=ax+b
y=ax+b为曲线
y
=
f
(
x
)
y=f(x)
y=f(x)的斜渐近线
快速求斜渐近线
若 y = f ( x ) = a x + b + α ( x ) , α ( x ) → 0 【线性函数+无穷小量】。则 y = f ( x ) 有斜渐近线 y = a x + b 若y=f(x)=ax+b+α(x),α(x)→0【线性函数+无穷小量】。则y=f(x)有斜渐近线y=ax+b 若y=f(x)=ax+b+α(x),α(x)→0【线性函数+无穷小量】。则y=f(x)有斜渐近线y=ax+b
6.平面曲线的曲率
曲率的定义:描述函数在一点处的弯曲程度。 K = lim Δ s → 0 ∣ Δ α Δ s ∣ K=\lim\limits_{Δs→0}|\dfrac{Δα}{Δs}| K=Δs→0lim∣ΔsΔα∣
曲率的计算: K = ∣ y ′ ′ ∣ ( 1 + y ′ 2 ) 3 2 K=\dfrac{|y''|}{(1+y'^2)^{\frac{3}{2}}} K=(1+y′2)23∣y′′∣
曲率半径: R = 1 K R=\dfrac{1}{K} R=K1
7.方程的根:存在性、个数
1.根的存在性
①方法一:零点定理
②方法二:罗尔定理
2.根的个数
①方法一:单调性
②方法二:罗尔定理推论
罗尔定理推论:若在区间 I \rm I I 上 f ( n ) ( x ) ≠ 0 f^{(n)}(x)≠0 f(n)(x)=0,则方程 f ( x ) = 0 f(x)=0 f(x)=0 最多有 n n n 个实根
3.做题步骤:
(1)构造函数,令
f
(
x
)
=
.
.
.
f(x)=...
f(x)=... 【则 原方程有根
⇔
\Leftrightarrow
⇔
f
(
x
)
=
0
f(x)=0
f(x)=0】
(2)求
f
′
(
x
)
f'(x)
f′(x),令
f
′
(
x
)
=
0
f'(x)=0
f′(x)=0,得驻点
(3)根据驻点分区间讨论单调性
8.函数不等式的证明
(1)证明不等式的5种常用方法
①单调性
②最大最小值
③拉格朗日中值定理
④泰勒公式
⑤凹凸性
(2)基本不等式
① 2 a b ≤ a 2 + b 2 2ab≤a^2+b^2 2ab≤a2+b2
② sin x < x < tan x , x ∈ ( 0 , π 2 ) \sin x<x<\tan x,x∈(0,\dfrac{π}{2}) sinx<x<tanx,x∈(0,2π)
③ x 1 + x < ln ( 1 + x ) < x , x ∈ ( 0 , + ∞ ) \dfrac{x}{1+x}<\ln(1+x)<x,x∈(0,+∞) 1+xx<ln(1+x)<x,x∈(0,+∞) ⇨ 1 n + 1 < ln ( 1 + 1 n ) < 1 n \dfrac{1}{n+1}<\ln(1+\dfrac{1}{n})<\dfrac{1}{n} n+11<ln(1+n1)<n1
④ 1 + x ≤ e x 1+x≤e^x 1+x≤ex
⑤放缩常用不等式:
∣
a
±
b
∣
≤
∣
a
∣
+
∣
b
∣
≤
2
max
{
∣
a
∣
,
∣
b
∣
}
|a±b|≤|a|+|b|≤2\max\{|a|,|b|\}
∣a±b∣≤∣a∣+∣b∣≤2max{∣a∣,∣b∣}