1. 快速排序的描述

1.1基本描述

  快速排序是一种时间复杂度为 O(n^2) 的排序算法。虽然最坏情况时间复杂度很差，但他的平均性能却很好，它的期望时间复杂度是 O(nlgn) 而且 O(nlgn) 中隐含的常数因子很小大约是1.44左右。
  快速排序与归并排序一样，也是基于归并的思想以下是对其子数组 A[ p…r ] 进行快速排序三步分治的过程：

分解：数组 A[ p…r ] 被划分为两个子数组 A[ p…q-1] 和 A[q+1…r]，使得 A[ p…q-1]中的每一个元素都小于等于 A[ q ] ，而 A[ q ]也小于等于 A[ q+1…r]中的每一个元素。

解决：通过递归调用快速排序，对子数组A[ p…q-1] 和 A[q+1…r]进行排序。

合并：因为子数组都是原址排序的，所以并不需要合并操作：A[ p…r ] 已经有序。

快速排序伪代码：

QUICKSORT(A,p,r)
    if p < r
        q = PARTITION(A, p ,r)
        QUICKSORT(A, p ,q-1)
        QUICKSORT(A, q+1 ,r)

其中，q = PARTITION(A, p ,r) 所执行的操作就是分解操作，并返回 q。

1.2 PARTITOION函数

​
PARTITION函数伪代码：

PARTITION(A, p, r) 
    x = A[r] 
    i = p - 1 
    for j = p to r - 1 
        do if A[j] ≤ x
            then i = i + 1 
            exchange A[i] with A[j] 
exchange A[i + 1] with A[r] 
return i + 1

PARTITION函数思路简介：

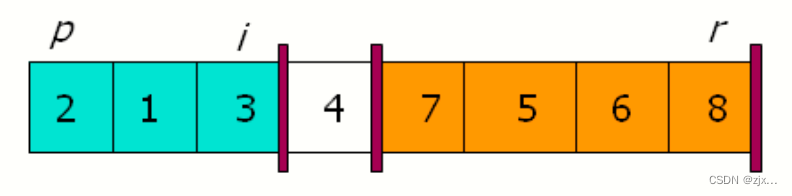
  其中 0 - i 维护的是小于等于A[ r ] 的序列，A[ i+1 ] 即为比 A[ r ] 大的第一个数，j从开始节点遍历到倒数第二个节点，遇到比 A[ r ] 小的数便进行 A[ j ] 与 A[ i+1 ] 的交换，以此维护了 0 - i 序列中比 A[ r ]小的特性。j 遍历完成后，即实现了A[0…i] 小于等于 A[ r ] ，A[i+1…j] 大于 A[ r ]。

PARTITION函数执行过程：

1.3 快速排序C++完整代码

# include <iostream>
using namespace std;
int PARTITION(int A[],int p,int r)
{
    int x = A[r];
    int i = p - 1;
    for(int j = p; j <= r - 1; j++)
    {
        if(A[j] <= x)
        {
            i = i + 1;
            swap(A[i],A[j]);
        }
    }
    swap(A[i+1] , A[r]);
    return i+1;
}
void QUICKSORT(int A[],int p,int r)
{
    if(p < r)
    {
        int q = PARTITION(A,p,r);
        QUICKSORT(A,p,q-1);
        QUICKSORT(A,q+1,r);
    }
}
int main()
{
    int A[100010];
    int n;
    cin>>n;
    for(int i=0;i<n;i++)
    {
        cin>>A[i];
    }
    QUICKSORT(A,0,n-1);
    for(int i=0;i<n;i++)
    {
        cout<<A[i]<<" ";
    }
    return 0;
}

2. 快速排序的性能

2.1 最坏时间复杂度

因为无法举出使快速排序达到最坏情况的例子所以我们通过两步证明其最坏时间复杂度为 O( n^2 )

1. 举一个例子证明其时间复杂度为 O( $n^2$)
   当对快速排序进行分解的过程中得到的结果为一部分为 n 个元素，另一部分为0个元素时，该例的运行时间递归式为：
   $$\begin{array}{rl}T(n)& =T(n-1)+T(0)+\theta (n)\\ & =T(n-1)+\theta (n)\end{array}$$可以得到：$$T(n)=\theta (n^2)$$
   由此可知， Quicksort 的最坏运行时间为： Ω( $n^2$)
2. 证明其时间复杂度不超过 O( $n^2$)
   设T(n)是对大小为 n 的输入进行快速排序的最坏情况时间，则有递归：
   $$T(n)=\underset{0\le q\le n-1}{\max }(T(q)+T(n-q-1))+C_{1}n$$我们猜测对于某个常数C使得T (n) ≤ C，将这个猜测代入上面的递推式，我们得到：
   $$\begin{array}{rl}T(n)& \le \underset{0\le q\le n-1}{\max }(C{q}^2+C(n-q-1{)}^2)+C_{1}n\\ & =C\ast \underset{0\le q\le n-1}{\max }(q^2+(n-1-q{)}^2)+C_{1}n\end{array}$$由于 $q^2+(n-1-q{)}^2$ 是 $q$ 的二次函数，求导可得，在区间 [1… n ] 范围内该函数只可能在 $q=1，q=n，q=n/4$，等三个点处取极值，由此可知：
   $$\sum _{0\le q\le n-1}(q^2+(n-1-q{)}^2)\le n^2$$所以有：
   $$T(n)\le C(n-1{)}^2+C_{1}n=C\ast n^2-2Cn+C_{1}n+C$$当取 C > C1 时，$T(n)<=C{n}^2$ 对所有 $n>=1$ 成立，由此证得快速排序时间复杂度不超过 O($n^2$)。

2.2 平均时间复杂度

  设 $T(n)$ 为输入规模为 n 时 QUICKSORT 算法的平均运行时间， $T_k(n)$为所选划分元序号为 k+1 时 QUICKSORT 算法的平均运行时间，则 $T(n)$ 满足以下递归方程：
$$T(n)=\sum _{k=0}^{n-1}(p(k+1)T_k(n))$$其中 $p(k+1)$为划分元素序号为$k+1$的概率，我们可以知道划分元素序号的概率是相同的故： $p(k+1)=\frac{1}{n}$，带入上式可得：
$$T(n)=\sum _{k=0}^{n-1}\frac{1}{n}{T}_k(n))=\frac{1}{n}\sum _{k=0}^{n-1}(T(k)+T(n-k-1)+cn)$$继续化简可得：
$$\frac{1}{n}(\sum _{k=0}^{n-1}T(k)+\sum _{k=0}^{n-1}T(n-k-1))+cn=\frac{2}{n}\sum _{k=0}^{n-1}T(k)+cn$$解递归方程可得：
$$nT(n)=2\sum _{k=0}^{n-1}T(k)+c{n}^2$$$$(n-1)T(n-1)=2\sum _{k=0}^{n-1}T(k)+c{n}^2$$两式相减，可得：
$$nT(n)-(n-1)T(n-1)=2T(n-1)+c(2n-1)$$$$\frac{T(n)}{n+1}<=\frac{T(n-1)}{n}+\frac{2c}{n}$$令
$$G(n)=\frac{T(n)}{(n+1)}$$则有：
$$\begin{array}{rl}G(n)& \le C(n-1)+\frac{2c}{n}\\ & =G(n-2)+2c(\frac{1}{n-1}+\frac{1}{n})\\ & =G(n-3)+2c(\frac{1}{n-2}+\frac{1}{n-1}+\frac{1}{n})\\ & =G(n-k)+2c(\frac{1}{n-k+1}+...+\frac{1}{n-1}+\frac{1}{n})\end{array}$$整理后得到：$$G(1)+2c\sum _{k=0}^{n-2}\frac{1}{n-k}=2c\sum _{k=2}^n\frac{1}{k}<=2c\ast H_n<=2clogn$$
所以，Quicksort 算法的平均时间复杂度为：$$T(n)=G(n)(n+1)=\theta (nlogn)$$

​