文章目录
- 参考:
- 总结
- [CSP-J 2021] 分糖果
- 题目背景
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- 样例 #2
- 样例输入 #2
- 样例输出 #2
- 样例 #3
- 样例输入 #3
- 样例输出 #3
- 提示
- 答案1
- 答案2-优化
- [CSP-J 2021] 插入排序
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- 提示
- 答案1
- 答案2
- 答案3
- 现场真题注意事项

参考:
https://www.luogu.com.cn/problem/P7909
总结
本系列为CSP-J/S算法竞赛真题讲解,会按照年份分析每年的真题,并给出对应的答案。本文为2021年真题。
https://www.luogu.com.cn/problem/list?tag=343&page=1
[CSP-J 2021] 分糖果
题目背景
红太阳幼儿园的小朋友们开始分糖果啦!
题目描述
红太阳幼儿园有 n n n 个小朋友,你是其中之一。保证 n ≥ 2 n \ge 2 n≥2。
有一天你在幼儿园的后花园里发现无穷多颗糖果,你打算拿一些糖果回去分给幼儿园的小朋友们。
由于你只是个平平无奇的幼儿园小朋友,所以你的体力有限,至多只能拿 R R R 块糖回去。
但是拿的太少不够分的,所以你至少要拿 L L L 块糖回去。保证 n ≤ L ≤ R n \le L \le R n≤L≤R。
也就是说,如果你拿了 k k k 块糖,那么你需要保证 L ≤ k ≤ R L \le k \le R L≤k≤R。
如果你拿了 k k k 块糖,你将把这 k k k 块糖放到篮子里,并要求大家按照如下方案分糖果:只要篮子里有不少于 n n n 块糖果,幼儿园的所有 n n n 个小朋友(包括你自己)都从篮子中拿走恰好一块糖,直到篮子里的糖数量少于 n n n 块。此时篮子里剩余的糖果均归你所有——这些糖果是作为你搬糖果的奖励。
作为幼儿园高质量小朋友,你希望让作为你搬糖果的奖励的糖果数量(而不是你最后获得的总糖果数量!)尽可能多;因此你需要写一个程序,依次输入 n , L , R n, L, R n,L,R,并输出你最多能获得多少作为你搬糖果的奖励的糖果数量。
输入格式
输入一行,包含三个正整数 n , L , R n, L, R n,L,R,分别表示小朋友的个数、糖果数量的下界和上界。
输出格式
输出一行一个整数,表示你最多能获得的作为你搬糖果的奖励的糖果数量。
样例 #1
样例输入 #1
7 16 23
样例输出 #1
6
样例 #2
样例输入 #2
10 14 18
样例输出 #2
8
样例 #3
样例输入 #3
见附件中的 candy/candy3.in。
样例输出 #3
见附件中的 candy/candy3.ans。
提示
【样例解释 #1】
拿 k = 20 k = 20 k=20 块糖放入篮子里。
篮子里现在糖果数 20 ≥ n = 7 20 \ge n = 7 20≥n=7,因此所有小朋友获得一块糖;
篮子里现在糖果数变成 13 ≥ n = 7 13 \ge n = 7 13≥n=7,因此所有小朋友获得一块糖;
篮子里现在糖果数变成 6 < n = 7 6 < n = 7 6<n=7,因此这 6 6 6 块糖是作为你搬糖果的奖励。
容易发现,你获得的作为你搬糖果的奖励的糖果数量不可能超过 6 6 6 块(不然,篮子里的糖果数量最后仍然不少于 n n n,需要继续每个小朋友拿一块),因此答案是 6 6 6。
【样例解释 #2】
容易发现,当你拿的糖数量 k k k 满足 14 = L ≤ k ≤ R = 18 14 = L \le k \le R = 18 14=L≤k≤R=18 时,所有小朋友获得一块糖后,剩下的 k − 10 k - 10 k−10 块糖总是作为你搬糖果的奖励的糖果数量,因此拿 k = 18 k = 18 k=18 块是最优解,答案是 8 8 8。
【数据范围】
| 测试点 | n ≤ n \le n≤ | R ≤ R \le R≤ | R − L ≤ R - L \le R−L≤ |
|---|---|---|---|
| 1 1 1 | 2 2 2 | 5 5 5 | 5 5 5 |
| 2 2 2 | 5 5 5 | 10 10 10 | 10 10 10 |
| 3 3 3 | 10 3 {10}^3 103 | 10 3 {10}^3 103 | 10 3 {10}^3 103 |
| 4 4 4 | 10 5 {10}^5 105 | 10 5 {10}^5 105 | 10 5 {10}^5 105 |
| 5 5 5 | 10 3 {10}^3 103 | 10 9 {10}^9 109 | 0 0 0 |
| 6 6 6 | 10 3 {10}^3 103 | 10 9 {10}^9 109 | 10 3 {10}^3 103 |
| 7 7 7 | 10 5 {10}^5 105 | 10 9 {10}^9 109 | 10 5 {10}^5 105 |
| 8 8 8 | 10 9 {10}^9 109 | 10 9 {10}^9 109 | 10 9 {10}^9 109 |
| 9 9 9 | 10 9 {10}^9 109 | 10 9 {10}^9 109 | 10 9 {10}^9 109 |
| 10 10 10 | 10 9 {10}^9 109 | 10 9 {10}^9 109 | 10 9 {10}^9 109 |
对于所有数据,保证 2 ≤ n ≤ L ≤ R ≤ 10 9 2 \le n \le L \le R \le {10}^9 2≤n≤L≤R≤109。
【感谢 hack 数据提供】
wangbinfeng
答案1
#include <bits/stdc++.h>
//#include<cstdio>//必须包含cstdio头文件
//#include<iostream>
using namespace std;
int main(){
freopen("candy.in","r",stdin);
freopen("candy.out","w",stdout);
int n,L,R,maxn=-1;
cin>>n>>L>>R;
for(int k=L;k<=R;k++)
{
maxn = max(maxn,k%n);
}
cout<<maxn<<endl;
//fclose(stdin);
//fclose(stdout);
return 0;
}
答案2-优化
#include <bits/stdc++.h>
//#include<cstdio>//必须包含cstdio头文件
//#include<iostream>
using namespace std;
int main(){
//freopen("candy.in","r",stdin);
//freopen("candy.out","w",stdout);
int n,L,R,maxn=-1;
cin>>n>>L>>R;
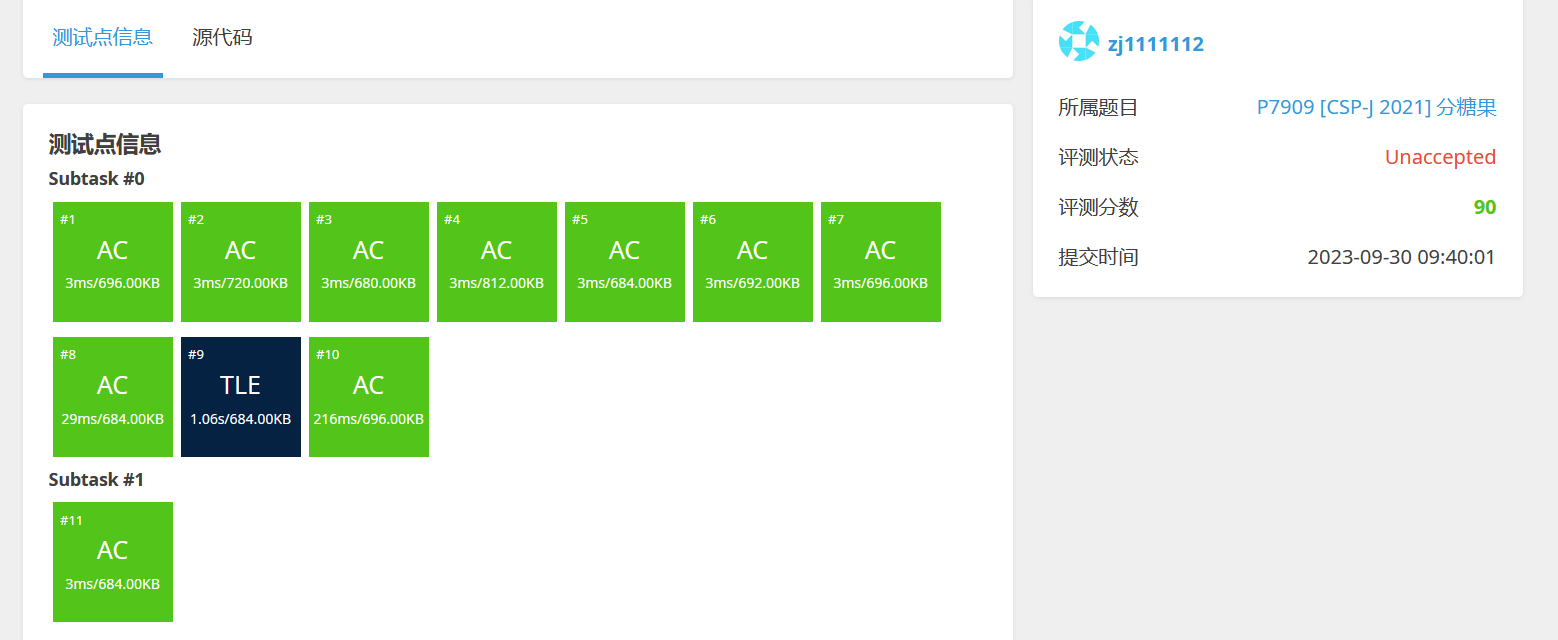
if(L%n+R-L >= n-1)
{
cout<<n-1<<endl;
}
else{
cout<<L%n + R - L<<endl;
}
//fclose(stdin);
//fclose(stdout);
return 0;
}
[CSP-J 2021] 插入排序
https://www.luogu.com.cn/problem/P7910
题目描述
插入排序是一种非常常见且简单的排序算法。小 Z 是一名大一的新生,今天 H 老师刚刚在上课的时候讲了插入排序算法。
假设比较两个元素的时间为 O ( 1 ) \mathcal O(1) O(1),则插入排序可以以 O ( n 2 ) \mathcal O(n^2) O(n2) 的时间复杂度完成长度为 n n n 的数组的排序。不妨假设这 n n n 个数字分别存储在 a 1 , a 2 , … , a n a_1, a_2, \ldots, a_n a1,a2,…,an 之中,则如下伪代码给出了插入排序算法的一种最简单的实现方式:
这下面是 C/C++ 的示范代码:
for (int i = 1; i <= n; i++)
for (int j = i; j >= 2; j--)
if (a[j] < a[j-1]) {
int t = a[j-1];
a[j-1] = a[j];
a[j] = t;
}
这下面是 Pascal 的示范代码:
for i:=1 to n do
for j:=i downto 2 do
if a[j]<a[j-1] then
begin
t:=a[i];
a[i]:=a[j];
a[j]:=t;
end;
为了帮助小 Z 更好的理解插入排序,小 Z 的老师 H 老师留下了这么一道家庭作业:
H 老师给了一个长度为 n n n 的数组 a a a,数组下标从 1 1 1 开始,并且数组中的所有元素均为非负整数。小 Z 需要支持在数组 a a a 上的 Q Q Q 次操作,操作共两种,参数分别如下:
1 x v 1~x~v 1 x v:这是第一种操作,会将 a a a 的第 x x x 个元素,也就是 a x a_x ax 的值,修改为 v v v。保证 1 ≤ x ≤ n 1 \le x \le n 1≤x≤n, 1 ≤ v ≤ 1 0 9 1 \le v \le 10^9 1≤v≤109。注意这种操作会改变数组的元素,修改得到的数组会被保留,也会影响后续的操作。
2 x 2~x 2 x:这是第二种操作,假设 H 老师按照上面的伪代码对 a a a 数组进行排序,你需要告诉 H 老师原来 a a a 的第 x x x 个元素,也就是 a x a_x ax,在排序后的新数组所处的位置。保证 1 ≤ x ≤ n 1 \le x \le n 1≤x≤n。注意这种操作不会改变数组的元素,排序后的数组不会被保留,也不会影响后续的操作。
H 老师不喜欢过多的修改,所以他保证类型 1 1 1 的操作次数不超过 5000 5000 5000。
小 Z 没有学过计算机竞赛,因此小 Z 并不会做这道题。他找到了你来帮助他解决这个问题。
输入格式
第一行,包含两个正整数 n , Q n, Q n,Q,表示数组长度和操作次数。
第二行,包含 n n n 个空格分隔的非负整数,其中第 i i i 个非负整数表示 a i a_i ai。
接下来 Q Q Q 行,每行 2 ∼ 3 2 \sim 3 2∼3 个正整数,表示一次操作,操作格式见【题目描述】。
输出格式
对于每一次类型为 2 2 2 的询问,输出一行一个正整数表示答案。
样例 #1
样例输入 #1
3 4
3 2 1
2 3
1 3 2
2 2
2 3
样例输出 #1
1
1
2
提示
【样例解释 #1】
在修改操作之前,假设 H 老师进行了一次插入排序,则原序列的三个元素在排序结束后所处的位置分别是 3 , 2 , 1 3, 2, 1 3,2,1。
在修改操作之后,假设 H 老师进行了一次插入排序,则原序列的三个元素在排序结束后所处的位置分别是 3 , 1 , 2 3, 1, 2 3,1,2。
注意虽然此时 a 2 = a 3 a_2 = a_3 a2=a3,但是我们不能将其视为相同的元素。
【样例 #2】
见附件中的 sort/sort2.in 与 sort/sort2.ans。
该测试点数据范围同测试点 1 ∼ 2 1 \sim 2 1∼2。
【样例 #3】
见附件中的 sort/sort3.in 与 sort/sort3.ans。
该测试点数据范围同测试点 3 ∼ 7 3 \sim 7 3∼7。
【样例 #4】
见附件中的 sort/sort4.in 与 sort/sort4.ans。
该测试点数据范围同测试点 12 ∼ 14 12 \sim 14 12∼14。
【数据范围】
对于所有测试数据,满足 1 ≤ n ≤ 8000 1 \le n \le 8000 1≤n≤8000, 1 ≤ Q ≤ 2 × 10 5 1 \le Q \le 2 \times {10}^5 1≤Q≤2×105, 1 ≤ x ≤ n 1 \le x \le n 1≤x≤n, 1 ≤ v , a i ≤ 1 0 9 1 \le v,a_i \le 10^9 1≤v,ai≤109。
对于所有测试数据,保证在所有 Q Q Q 次操作中,至多有 5000 5000 5000 次操作属于类型一。
各测试点的附加限制及分值如下表所示。
| 测试点 | n ≤ n \le n≤ | Q ≤ Q \le Q≤ | 特殊性质 |
|---|---|---|---|
| 1 ∼ 4 1 \sim 4 1∼4 | 10 10 10 | 10 10 10 | 无 |
| 5 ∼ 9 5 \sim 9 5∼9 | 300 300 300 | 300 300 300 | 无 |
| 10 ∼ 13 10 \sim 13 10∼13 | 1500 1500 1500 | 1500 1500 1500 | 无 |
| 14 ∼ 16 14 \sim 16 14∼16 | 8000 8000 8000 | 8000 8000 8000 | 保证所有输入的 a i , v a_i,v ai,v 互不相同 |
| 17 ∼ 19 17 \sim 19 17∼19 | 8000 8000 8000 | 8000 8000 8000 | 无 |
| 20 ∼ 22 20 \sim 22 20∼22 | 8000 8000 8000 | 2 × 1 0 5 2 \times 10^5 2×105 | 保证所有输入的 a i , v a_i,v ai,v 互不相同 |
| 23 ∼ 25 23 \sim 25 23∼25 | 8000 8000 8000 | 2 × 1 0 5 2 \times 10^5 2×105 | 无 |
答案1
#include <bits/stdc++.h>
//#include<cstdio>//必须包含cstdio头文件
//#include<iostream>
using namespace std;
struct node
{
int id,num;
}a[8010];
int n,q;
bool cmp(node a,node b)
{
if(a.num == b.num){
return a.id<b.id;
}else{
return a.num<b.num;
}
}
int main(){
//freopen("candy.in","r",stdin);
//freopen("candy.out","w",stdout);
scanf("%d%d",&n,&q);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i].num);
a[i].id = i;
}
sort(a+1,a+1+n,cmp);
// cout<<"*****"<<endl;
// for(int i=1;i<=n;i++)
// {
// cout<<a[i].id<<" "<<a[i].num<<endl;
// }
int op,u,v;
while(q--){
scanf("%d",&op);
if(op == 1){//修改
scanf("%d%d",&u,&v);
//找到值,进行修改,排序
for(int i=1;i<=n;i++){
if(a[i].id==u){
a[i].num = v;
break;
}
}
sort(a+1,a+1+n,cmp);
}else{//查找
scanf("%d",&u);
for(int i=1;i<=n;i++){
if(a[i].id==u){
printf("%d\n",i);
break;
}
}
}
}
// system("pause");
//fclose(stdin);
//fclose(stdout);
return 0;
}
答案2
#include <bits/stdc++.h>
//#include<cstdio>//必须包含cstdio头文件
//#include<iostream>
using namespace std;
struct node
{
int id,num;
}a[8010];
int n,q;
int b[8010];// 用来保存原来的下标和现在的下标
bool cmp(node a,node b)
{
if(a.num == b.num){
return a.id<b.id;
}else{
return a.num<b.num;
}
}
int main(){
//freopen("candy.in","r",stdin);
//freopen("candy.out","w",stdout);
scanf("%d%d",&n,&q);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i].num);
a[i].id = i;
}
sort(a+1,a+1+n,cmp);
for(int i=1;i<=n;i++){
b[a[i].id] = i;//
}
// cout<<"*****"<<endl;
// for(int i=1;i<=n;i++)
// {
// cout<<a[i].id<<" "<<a[i].num<<endl;
// }
int op,u,v;
while(q--){
scanf("%d",&op);
if(op == 1){//修改
scanf("%d%d",&u,&v);
//找到值,进行修改,排序
// for(int i=1;i<=n;i++){
// if(a[i].id==u){
// a[i].num = v;
// break;
// }
// }
a[b[u]].num=v;
sort(a+1,a+1+n,cmp);
// 新增
for(int i=1;i<=n;i++){
b[a[i].id]=i;
}
}else{//查找
scanf("%d",&u);
// for(int i=1;i<=n;i++){
// if(a[i].id==u){
// printf("%d\n",i);
// break;
// }
//
// }
printf("%d\n",b[u]);
}
}
// system("pause");
//fclose(stdin);
//fclose(stdout);
return 0;
}
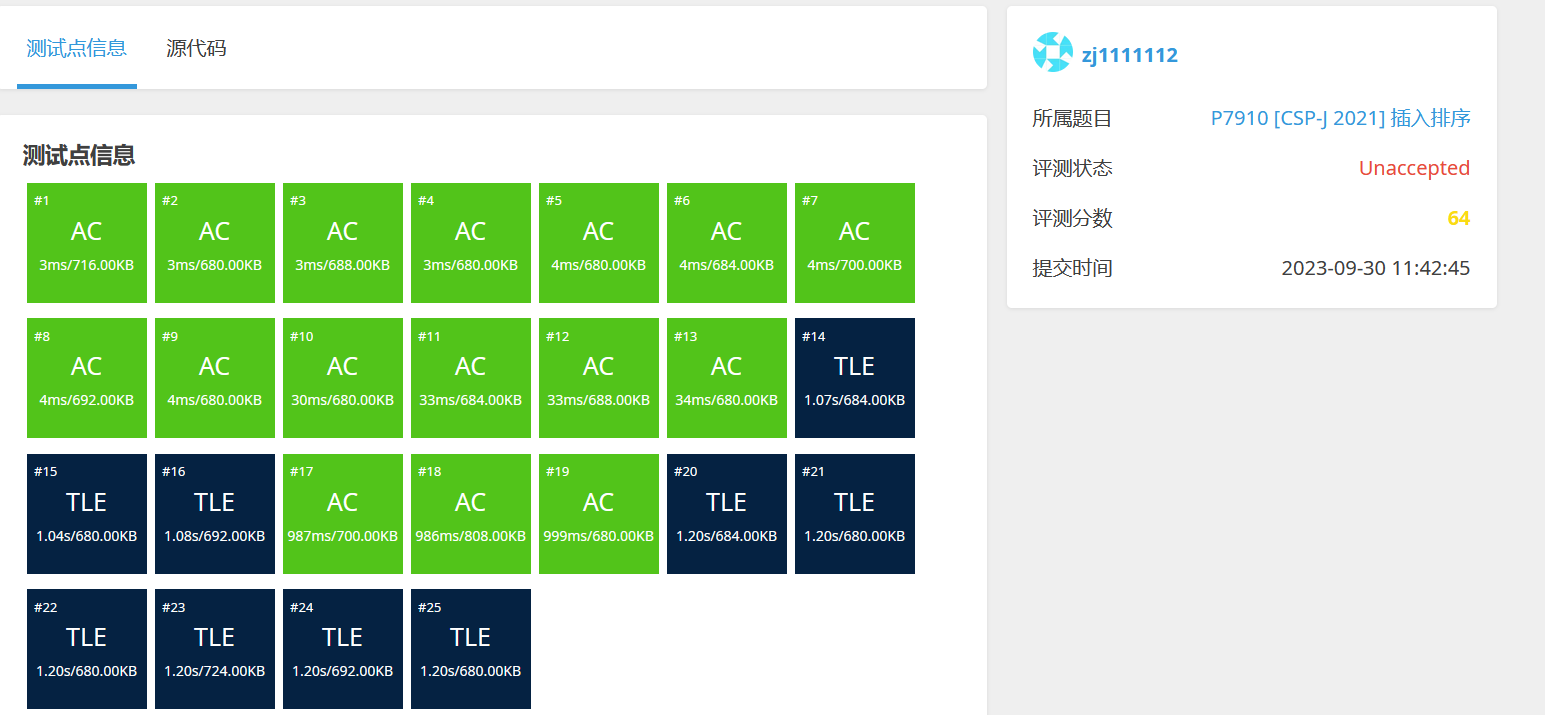
答案3
#include <bits/stdc++.h>
//#include<cstdio>//必须包含cstdio头文件
//#include<iostream>
using namespace std;
struct node
{
int id,num;
}a[8010];
int n,q;
int b[8010];// 用来保存原来的下标和现在的下标
bool cmp(node a,node b)
{
if(a.num == b.num){
return a.id<b.id;
}else{
return a.num<b.num;
}
}
void change(int pos){
while(pos > 1){
if(a[pos].num>a[pos-1].num) break;
if(a[pos].num==a[pos-1].num && a[pos].id>a[pos-1].id) break;
swap(a[pos],a[pos-1]);
b[a[pos].id]=pos;
pos--;
}
while(pos<n){
if(a[pos].num<a[pos+1].num) break;
if(a[pos].num==a[pos+1].num && a[pos].id<a[pos+1].id) break;
swap(a[pos],a[pos+1]);
b[a[pos].id]=pos;
pos++;
}
b[a[pos].id]=pos;
}
int main(){
//freopen("candy.in","r",stdin);
//freopen("candy.out","w",stdout);
scanf("%d%d",&n,&q);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i].num);
a[i].id = i;
}
sort(a+1,a+1+n,cmp);
for(int i=1;i<=n;i++){
b[a[i].id] = i;//
}
// cout<<"*****"<<endl;
// for(int i=1;i<=n;i++)
// {
// cout<<a[i].id<<" "<<a[i].num<<endl;
// }
int op,u,v;
while(q--){
scanf("%d",&op);
if(op == 1){//修改
scanf("%d%d",&u,&v);
//找到值,进行修改,排序
// for(int i=1;i<=n;i++){
// if(a[i].id==u){
// a[i].num = v;
// break;
// }
// }
a[b[u]].num=v;
change(b[u]);
// sort(a+1,a+1+n,cmp);
// // 新增
// for(int i=1;i<=n;i++){
// b[a[i].id]=i;
// }
}else{//查找
scanf("%d",&u);
// for(int i=1;i<=n;i++){
// if(a[i].id==u){
// printf("%d\n",i);
// break;
// }
//
// }
printf("%d\n",b[u]);
}
}
// system("pause");
//fclose(stdin);
//fclose(stdout);
return 0;
}
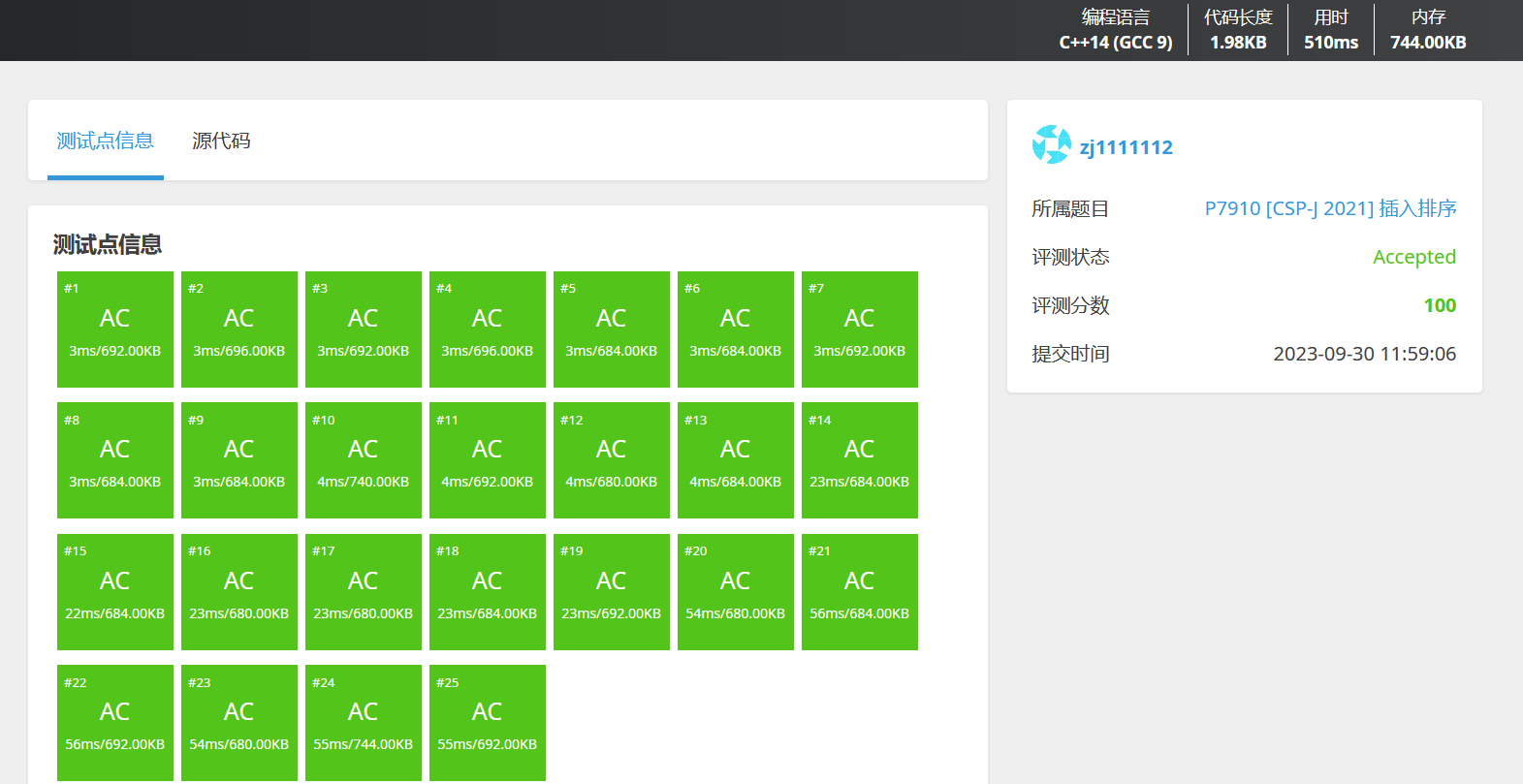
现场真题注意事项
https://cspoj.com/contest.php?cid=1002
Fus5yz4x3EcSJH1Z
注意事项
- 文件名(程序名和输入输出文件名)必须使用英文小写。(提交必须使用freopen()进行提交)
- C/C++ 中函数 main() 的返回值类型必须是 int,程序正常结束时的返回值必须是0。
- 提交的程序代码文件的放置位置请参考各省的具体要求。
- 因违反以上三点而出现的错误或问题,申述时一律不予受理。
- 若无特殊说明,结果的比较方式为全文比较(过滤行末空格及文末回车)。
- 程序可使用的栈空间内存限制与题目的内存限制一致。
- 全国统一评测时采用的机器配置为:Inter® Core™ i7-8700K CPU @3.70GHz,内存 32GB。上述时限以此配置为准。
- 只提供 Linux 格式附加样例文件。
- 评测在当前最新公布的 NOI Linux 下进行,各语言的编译器版本以此为准
/*
假设输入样例数据存在文件test.in中,输出样例数据存在文件test.out中,
则在CSP、NOI等比赛的代码中,需添加freopen、fclose语句,
内容详见模板代码如下。
*/
#include <bits/stdc++.h>
#include<cstdio>//必须包含cstdio头文件
#include<iostream>
using namespace std;
int main(){
freopen("test.in","r",stdin);
freopen("test.out","w",stdout);
cout<<"Hello NOI"<<endl;
fclose(stdin);
fclose(stdout);
return 0;
}
下面为函数的简介,详细可参见 http://www.cplusplus.com/reference/clibrary/cstdio/freopen.html
函数名:freopen
声明:FILE *freopen( const char *path, const char *mode, FILE *stream );
所在文件: stdio.h
参数说明:
path: 文件名,用于存储输入输出的自定义文件名。
mode: 文件打开的模式。和fopen中的模式(如r-只读, w-写)相同。
stream: 一个文件,通常使用标准流文件。
返回值:成功,则返回一个path所指定文件的指针;失败,返回NULL。(一般可以不使用它的返回值)
功能:实现重定向,把预定义的标准流文件定向到由path指定的文件中。标准流文件具体是指stdin、stdout和stderr。其中stdin是标准输入流,默认为键盘;stdout是标准输出流,默认为屏幕;stderr是标准错误流,一般把屏幕设为默认。通过调用freopen,就可以修改标准流文件的默认值,实现重定向。
#include<iostream>
#include<cstdio>
using namespace std;
int main(){
freopen("7532.in", "r", stdin);
freopen("7532.out", "w", stdout);
//原来的代码保持不变
double a, b, r;
int k;
cin >> a >> b;
k = int(a/b);
r = a - b * k;
printf("%g", r);
//-------------
fclose(stdin);
fclose(stdout);
return 0;
}