文章目录
- 从方法论上来讲
- 从问题范式上来讲
- 从研究对象来讲

Hi,你好。我是茶桁。
上一章中,我们谈论了人工智能在时间维度上的不同时间不同的侧重点,这只是一个片面的方面。当然除此之外,我们还要从其他方向来认识人工智能,才能更加的全面。
那下面,我们就分别从方法论,问题范式和研究对象来分别认识一下人工智能,看看有没有什么不一样的心得。
从方法论上来讲
接下来大家来讲从方法论上来看待人工智能。
方法论就是一件问题其实用不同的方法都可以解决,一件问题用不同的方法都可以解决。同样的一个问题,不同的人说的是不一样的。
在整个人工智能的历史上,此起彼伏的一直有两种方法在做:一种叫做基于统计的,一种叫做基于逻辑分析的。
Statistical vs Logic analysis

上节课给大家举的李开复的那个例子,当时人们是希望通过语法树,希望能够写程序去分析语法术来解决,结果发现越做越难。
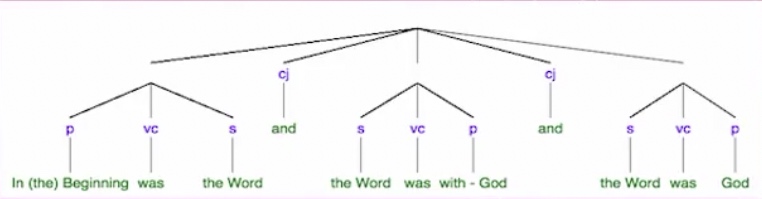
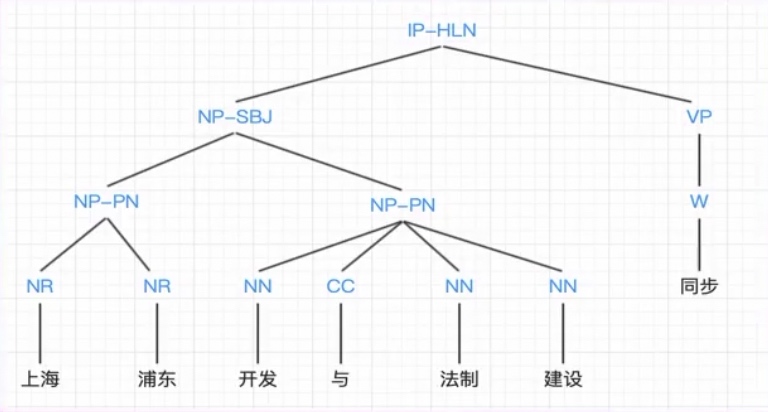
后来人们就把它变成了基于统计去做,统计就简单了,只要我数一下出现的频率就可以了。
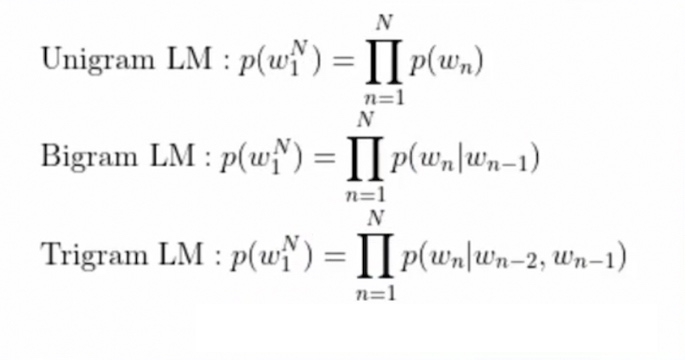
这就是这两个学派,现在是统计学派占优势。
从1990年开始到现在,基本上是统计学派占优势。我们之后要学习的,从第5节课开始,基本上学习的最主流的80%-90%的内容都是基于统计的方法。
但是逻辑的分析方法依然存在,而且如果你以后要做NLP自然语言处理,或者做计算机视觉等等,都会遇到这种逻辑类。
待会咱们会来出一道题,我们一起来动手去完成它。就是我们怎么样来生成一个句子。
逻辑和统计的区别非常大,我们如何让计算机生成语言。这个问题其实是当时要做图灵测试非常非常重要的一个能力。包括现在做什么小爱机器人,大家可以拿这个电话去打你最近的海底捞,你会发现海底捞现在基本上100%都是机器人在回答了。
那么现在我们摆出来了一个问题,就是机器怎么生成语言?
今天就跟大家来讲解, 这是一个非常古老人工智能方法。但是是一个非常非常具有代表性的,大家可以通过他来看到人工智能的多样性。
我们可能之后学习的时候,从第5课学的都是基于统计的方法,但是我们今天要给大家说的是,历史上有很多种方法非常有用。最近虽然不是占主流,但是大家在需要的时候一定要想起它,它能解决你很多很重要的问题。
而且在这个过程中为什么我们提出来了这些新的深度学习方法,也能知道到底哪些东西是解决不了的。
OK,我们现在来看一下这个问题:计算机如何能够生成像人类一样的语言。
当时人们想了很多种方法,有很多人知道,现在用什么LSTM,GPT-4等等去做。
它们来做语言生成很好,但是我们来跟大家看看当年人们是怎么样解决这个问题的,曾经一度非常重要的一种方法。
有人他定义了一个东西, 比方说我们现在知道了一个grammar
grammar = """
句子 = 主 谓 宾
谓 = 吃 | 喝 | 玩
宾 = 皮球 | 桃子
主 = 你 | 我 | 他
"""
假设我们现在有一个东西叫做「句子」,大家都知道这个句子是主、谓、宾生成的,主语、谓语、宾语。
然后我们这个谓语就是动词,比方说吃|喝|玩,宾语比如说皮球|桃子,然后主语就是你|我|他。
曾经有一段时间,人们为了解决这个问题,写了这样的东西。
import random
def generate_verb():
return random.choice('吃|喝|玩|'.split('|'))
def 生成宾语():
return random.choice('皮球|桃子'.split('|'))
print(生成宾语()+generate_verb())
---
桃子玩
大家看,这是非常非常原始,非常非常古老的一种写法。当时人们想利用模板解决问题,最简单的方法。但是人们发现一个问题,就是假如说我们这里的谓语动词有个变化,比如说我们要再加一个动词,或者我们要在这里的宾语再加一个东西:
grammar = """
句子 = 主 谓 宾
谓 = 吃 | 喝 | 玩 | 打
宾 = 皮球 | 桃子 | 饺子
主 = 你 | 我 | 他 | 她
"""
这样的话,就意味着我们每修改一下这个语法,是不是原代码也要操作?
import random
def generate_verb():
return random.choice('吃|喝|玩|打'.split('|'))
def 生成宾语():
return random.choice('皮球|桃子|饺子'.split('|'))
print(generate_verb()+生成宾语())
---
吃饺子
如果这样的话,代码整合起来就很复杂。而且我们有可能还要说别的话,例如我们在这里的说一个招待,招待的场景就等于打招呼。
grammar2 = """
招待 = 打招呼 玩 活动 吗?
打招呼 = 你好 | 您好 | 好久不见
玩 = 需要玩 | 喜欢玩 | 想玩
活动 = 骑马 | 打球 | 喝茶
"""
你看,我们如果还有另外的一个句子,想把它生成这样的话,意味着又得重新再写一套程序。才能解决grammar2的这个问题。
这个东西看起来很简单,但其实它会越来越难。如果说我们现在有个grammar2,又要再重新写很多句子。
这个时候最古老的一批程序员们就希望:“我能不能不要每次都改写代码,每次代码都不要改了?你给我不同的输入我能接受,代码不经过改动、就能解决这个问题。”
这个思想其实是我们站在程序员视角,程序员思考的人工智能其实是最接近这种想法。
假如说把一张图片要做到识别率99%那是很简单的,要把两张图片做到90%也是很简单的,专门写一个程序就行。但是怎么样做到每次改了图片之后,还能做到99%呢?这是我们需要讨论问题。这个朴素的想法一直延伸到现在。
怎么解决这个问题呢?这个时候就需要抽象了。怎么抽象呢?
我们现在把它变成一行一行:
for line in grammar.split('\n'):
if not line.strip(): continue
print(line)
---
句子 = 主 谓 宾
谓 = 吃 | 喝 | 玩
宾 = 皮球 | 桃子
主 = 你 | 我 | 他
然后再留一个grammar,我们把它变成一个表达式:
grammar_gen = dict()
for line in grammar.split('\n'):
if not line.strip(): continue
print(line)
stmt, expr = line.split('=')
grammar_gen[stmt] = expr
print(grammar_gen)
---
句子 = 主 谓 宾
谓 = 吃 | 喝 | 玩
宾 = 皮球 | 桃子
主 = 你 | 我 | 他
{'句子 ': ' 主 谓 宾', '谓 ': ' 吃 | 喝 | 玩', '宾 ': ' 皮球 | 桃子', '主 ': ' 你 | 我 | 他'}
就是statement,期望表达的东西,和expression。
首先我们把每个grammar变成了一个Dictionary,那么如果能够有一种东西通过Dictionary来生成的话,它是不是就可以输入不同的grammar street形式。
grammar_gen = dict()
for line in grammar.split('\n'):
if not line.strip(): continue
print(line)
stmt, expr = line.split('=')
expressions = expr.split('|')
grammar_gen[stmt.strip()] = [e.strip() for e in expressions]
print(grammar_gen)
---
句子 = 主 谓 宾
谓 = 吃 | 喝 | 玩
宾 = 皮球 | 桃子
主 = 你 | 我 | 他
{'句子': ['主 谓 宾'], '谓': ['吃', '喝', '玩'], '宾': ['皮球', '桃子'], '主': ['你', '我', '他']}
谓语后面跟的是一个list, 宾语也是这样。
现在来写一个很有趣的一个代码。
def generate_sentence(gram, target='句子'):
if target not in gram: return target
exp = random.choice(gram[target])
return ''.join([generate_sentence(gram, e) for e in exp.split()])
print('generated: \n'+generate_sentence(grammar_gen))
---
generated:
我吃桃子
我们来看一下这段代码,如果我们现在要根据这样的一个Dictionary来生成句子,怎么来生成句子呢?这是一个当年很经典的一个程序。
如果我们的一个target它在grammar的key里边,那么我们就证明现在需要去扩展,如果他不在我们的key里边,我们就说他不需要扩展,直接返回就可以了。
if target not in garm: return target
如果他在这个key里边我们怎么扩展呢? 比方说我们在这里收一个句子, 它等于主谓宾, 先要扩展主语, 再扩展谓语, 再扩展宾语。
扩展它的时候,就需要随机去选择一个去扩展的表达式。选择这个表达式之后,按照空格分割生成很多个小的表达式,再把这个小的表达式再次进行生成。
generate_sentence(gram, e) for e in exp.split()
generate_sentence(grammar_gen)就会生成一句话,当然是随机的,这次我们生成的是:“我吃桃子”。
那么这样的好处是什么?
我们现在来封装一个方法get_grammar, 将之前对grammar的处理封装进去, 然后我们再修改下generate_sentence方法,之后再打印的时候,我们可以尝试将之前定义的grammar2代入进去,只不过我们需要将之前写的招待修改为句子, 因为我们判断target是句子,完整代码如下:
grammar = """
句子 = 主 谓 宾
谓 = 吃 | 喝 | 玩
宾 = 皮球 | 桃子
主 = 你 | 我 | 他
"""
grammar2 = """
句子 = 打招呼 玩 活动 吗?
打招呼 = 你好 | 您好 | 好久不见
玩 = 需要玩 | 喜欢玩 | 想玩
活动 = 骑马 | 打球 | 喝茶
"""
def get_grammar(grammar_string):
grammar_gen = dict()
for line in grammar_string.split('\n'):
if not line.strip(): continue
stmt, expr = line.split('=')
expressions = expr.split('|')
grammar_gen[stmt.strip()] = [e.strip() for e in expressions]
return grammar_gen
def generate_sentence(gram, target='句子'):
if target not in gram: return target
exp = random.choice(gram[target])
return ''.join([generate_sentence(gram, e) for e in exp.split()])
print('generated: \n'+generate_sentence(get_grammar(grammar)))
print('generated: \n'+generate_sentence(get_grammar(grammar2)))
---
generated:
你吃桃子
generated:
你好需要玩骑马吗?
在这里就可以做到, 写了一个grammar, 打印结果为「你吃桃子」,接下来变成grammar2, 打印出来就是「你好需要玩骑马吗?」
是不是很有意思?我们做到改变了输入,程序没有改,他能接受新的输入,都是随机的。
这就是站在程序员视角,当时研究人工智能AI最渴望的就是不需要改变程序了。
下面我们再修改一下grammar, 给他加上复合句子,起名为句子,将之前的句子修改为Single句子, 简写为s_句子
grammar = """
句子 = s_句子 , 连词 句子 | s_句子
连词 = 而且 | 但是 | 不过
s_句子 = 主语 谓语 宾语
主语 = 你| 我 | 他
谓语 = 吃| 玩
宾语 = 桃子| 皮球
"""
这样修改之后,大家觉得会发生什么事情呢?我们还是使用之前的代码,代码不变,然后我们可以得到:
---
generated:
你吃桃子,不过你吃皮球,不过你玩桃子,但是你吃皮球,但是他玩皮球,而且他玩皮球
generated:
您好喜欢玩打球吗?
他可以产生更加长、更加复杂的句子。
如果我们再加一个判断句子概率的东西, 就能够生成更像句子的句子了。
就是之前讲的,李开复在一九八几年探索出来的一种东西,能够去判断一个句子出现的概率。那么当这个程序出现很多句子的时候,我们就能做个判断,给他做个排序、做个打分,就能够知道哪个句子的概率最大了。
这个程序厉害的点不在于它采用了什么非常高科技的方法,而是在这个时候提出来的一种思想,这个思想就是问题的输入变化了,但是我们的代码希望不要变,我们的程序不希望变。这个是这个程序最主要的一个特点。
以后咱们整个课程上,机器学习等等代码,其实都是冲着这一个目标去的。
当时基于这个规则的程序其实也没有那么好写。大家看一下上面这段程序,其实看起来好像很短,但是一个人如果想靠自己的脑力思考出来这样的程序,你会发现并不简单。
这段代码当然不是我原创的,如果你想原创的去解决这个问题其实很复杂。就这也是为什么后来通过这种逻辑分析规则方法没有再进行下去的原因,因为它太复杂了。
这是咱们的第一个案例,目的是希望大家知道AI写程序的目的是什么,也希望大家知道有一种方法,只不过最近几年他不太火了,但是曾经产生过很多很重要的方法。
刚刚给大家讲过基于统计的方法,我们判断一句话的概率,会把它变成一组词的概率去统计,也可以变成一个数形的东西。
那么大家现在想想,基于统计和基于逻辑推理这两种方法,他们有什么特点?有什么优缺点呢?
统计永远达不到100%的准确,基于逻辑的灵活性差、代码很复杂。
从问题范式上来讲
好,接下来呢,我们再从另外一个问题的角度来分析一下:从问题范式上。
什么叫做问题范式?
方法论,就是准备用什么东西去解决它,到底用统计,还是用分析的方法去解决它。
所谓的问题范式就是Paradigm,其实和方法论类似。只不过它又把问题分成了不同的类型。
第一种类型叫做Relax based。

解决起来对于人类来说很轻松,比方说这张图里,公交车在哪。

我们一眼就指出来了对不对? 或者问左边亮的是红灯还是绿灯?我们一眼就看出来了。
大家一定要清楚一个概念,准则就是人觉得越简单的问题,对于计算机来说越复杂。让计算机去判断这个地方的车在哪里,这个地方的红灯到底表示什么意思,其实是很复杂的一个事情。

这张图里,哪边是狗,哪边是猫,对我们人类来说是So easy的一个问题。那这种问题,就叫做Relax based。
还有一类情况叫做State based。

在这局对局中,假如你是红方,你该怎么走?
这个问题我们要思考的时候,和前面就会发现不一样了。前面是看一眼就能懂,而这个你得经过思考,思考你现在在什么状态,走了之后会怎么样。在脑子里面要思考一系列问题。
现在AI主要解决的问题是第一种问题,是Relax based。后面这种State based问题解决的不多,但是其实是现在迫切急需解决的问题。AlphaGo其实解决了一部分, 但是它也是需要大量的算力,大量的训练样本。
再比如,从齐齐哈尔到鄂尔多斯这两个地方我开车怎么去。
你要看到地图也不能一下子就知道,也得一个一个点去看。这种问题就是一个典型的我们需要考虑现在在什么情况,做了之后,下一个状态会是什么情况的问题。
再下一种情况叫做优化模型。

什么叫优化模型?比方说一个工厂就这么多时间这么多人力,我怎么样让这个工厂现在产出最大的金额,在一个固定的范围之内,固定的约束条件之下要得到一个最优质的答案。
这也是一种很典型的AI问题,给一个复杂函数,怎么样找到这个函数的最优点?这也是一类情况。
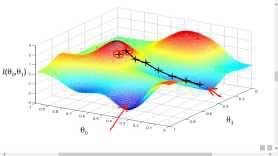
美团外卖的小哥,怎么样能够让他最快的接到单子,怎么样给他策划一个线路,让他最快的能够送达,这就是属于这样的一个问题。
除此之外,还有一类情况叫做纯推理问题。
这个其实也是人们一直在期望解决,但是现在解决的情况也不好。
比方说,下过雨天地面就会湿,那么现在我告诉你地面湿了,问你下过雨没。机器就应该自动知道下过雨。
这个问题现在难点是难在,首先人类社会中有大量的场景需要这个,在医学上、在法律上、保险上。但是用机器学习的方法现在不好做,效果很差。人们各种探索做的也不太好。
斯坦福大学为了掩饰这个问题写了一个简单程序,但是也只能解决非常非常基础的问题。


注释:此截图来自于地址:https://stanford-cs221.github.io/autumn2020/assignments/logic/index.html
在这些问题的类型里边,Relax based model是现在AI解决的最多的, 图像分类识别。接下来就是优化问题,应用的也比较多。State based model会用到一些,比如说滴滴打车,其实我们常用的就有高德导航。最难的是逻辑推理,逻辑推理的问题很难做。
接下来,讲解一下什么叫做State based model。出这么一道问题,一道很典型的智力题。很多人不太理解我们State besed model是解决什么问题,我们先来做一道智力题。

现在有两个杯子,左边的杯子是90毫升,右边的杯子是40毫升的。

现在这边有个水池,水池有个水龙头可以接水。现在我问个问题,如何得到50毫升的水?
很简单对吧?拿90的杯子去给它装满,然后我们再不断的倒水,把90往40里倒,
40的倒满之后,90里剩下的就是50。
那我再问一下,如何得到60毫升的水?或者我们问,通过这样的方法能得到60毫升的水吗?
这个问题是不是看着就很难?那能不能得到65?能不能得到70?能不能得到30呢?
或者,现在告诉你大杯子是60,小杯子是40,我们能不能得到70的水呢?假设我们这里有5个杯子,一个杯子是3,一个杯子是7,一个杯子是13,一个杯子是17,然后还有一个杯子是25,我们如何得到18?
是不是很奇怪?想问解决这个问题有什么意义?这个问题其实代表了很多所谓的需要推理的智力题。就是今天要跟大家说的,是一种通用的方法。
那么我们再思考一下,我们再变个问题。假如说两边中间有条河,有有五个人,现在是晚上,有一个手电筒,要把这五个人从左边全部运到右边。现在想让计算机告诉我们一次过。
我们标好ABCDE,第一次把a和b过去,然后呢a再过来,再把c接回去等等。让计算机解决这样的问题。
再来一个经典的问题,传教士和食人族。就是有一群传教士带了一群食人族的人,他们要过一条小河,左边和右边必须满足一种情况,传教士的人数必须大于等于食人族的人数,否则食人族就会把传教士给吃了,船上也是。
传教士的人数在岸边和船上都大于等于食人族的人数,要不然就会被吃了。那问你,如果现在给你n个食人族m个传教士,你怎么样制定一个策略把它移过去?
现在的问题是,我们要让计算机来解决这两个问题。这种问题就是典型的State based model。
这几个问题,看起来都有类似的过程。都是我们现在在一个情况下,要达到另外的一个情况下,我怎么样到达?我们现在要知道的是它的路径是什么。就这几个问题,共同点都是要知道路径是什么。
那我们来分析一下,怎么解决这个问题。
如果大家想到一个数学方法来解决这非常的好,但是我想告诉大家,我们现在是学习人工智能的课程,以后遇到这种的问题的思考方向一定是你要想一种办法让机器自动能解决。就是你要想的是机器自动解决这个问题的方法,而不是我们要花心思去找到这个答案。
这个是你和一个参加奥数的学生的区别,我们要让机器自动解决这个问题,这是咱们学习这个的工作。
我们来看看咱们怎么样解决这个问题。
这个问题抽象一下就是我们在一种状态a下,要达到另外一种状态b。我们期望能解决问题现在最简单的就是,首先我们需要用一种方法来表示状态,如果是两杯水的问题,可以用一个二元数组(B1, B2)来表示现在这个状态。
假如说我们这里是(0,0), 要变到(x,6)或者(6, x)。
这个就和下棋,走地图一摸一样。如果从a这一步开始能够知道下一步有哪些状态,然后在下一步我们又知道再下一步有哪些状态。我们继续这样扩展下去,机器就可以找到一点。如果我们让机器去把这个图做个遍历,就能从a点找到b点。
倒水问题和下棋、地图,以及我们做决策都很类似。都是有一个状态
之后,要看到接下来的状态是哪些,再接下来之后再去思考一步一步的。
现在来看一下,如果对于任意的一个状态(x,y)我们已知,已知这两个杯子的大小是(X,Y),对于任意一个状态(x,y)。 它会有哪些状态呢?
第一个状态可能是(0, y), 也就是x清零。
第二个状态可以是(x,0)。
也就是就是我从(X,Y)可以到(0,y)和(x,0)这两种状态。
第三种还可以把X灌满,就是(X,y)。
第四种可以把y灌满,就是(x,Y).
那第一种就是把x清空了,第二种就是把y清空了,第三种是把x灌满,第四种是把y灌满。
除了这几个状态之外,还有那些状态我们没有说?我们没说互相倒水的情况。
那第五个状态就是(0, x+y), 也就是将x的水倒入y中。不知道大家发觉没有,这第五个状态有个坑,把x倒给y,能这样做是因为x+y是小于等于Y才可以。如果不是的,这里其实就变成了(x+y-Y, y)。
同理第六个状态是我们把y倒给x,也就是(x+y,0),需要x+y <= x,如果不是的,这里把X倒满了, y的状态就应该是x+y-X,那就变成(X, x+y-X)。
每一个状态就和走象棋很像,每个象棋后边都有一个状态。坐车也是一样,每到一站下一步有不同的路线。
在这里,其实就是每个状态会接6个状态。然后让机器自动去找一遍就可以了。
那咱们来解决一下这个问题,把它实现一下。
def successors(x, y, X, Y):
return{
(x, 0): '倒空y',
(0, y): '倒空x',
(x, Y): '装满y',
(X, y): '装满x',
(0, x+y) if x+y <= Y else (x+y-Y, Y): 'x => y',
(x+y, 0) if x+y <= X else (X, x+y-x): 'y => x',
}
print(successors(30,40,90,40))
---
{(30, 0): '倒空y', (0, 40): '倒空x', (30, 40): 'x => y', (90, 40): '装满x', (70, 0): 'y => x'}
这样,我们就写出了返回状态的一个方法。其中x,y是当前杯子的状态,X,Y是我们已知的杯子状态,也就是最大可装多少水。
然后我们将当前的x,y设置为(30,40),然后我们就可以输出在这种情况下会有怎样的一些状态。
我们就能够找到它的解法了,就能够找到它的答案了。也知道我们需要写一个程序搜索。
我们来看一下这个问题的输入, 输入分别是capacity1,capacity2,表示两个杯子的容量。然后还有期望得到的目标goal, 以及它初始状态时候的值start, 如果不专门的声明, 就给他默认成是0。
如果目标已经在初始状态了, 那我们就把这个初始状态返回就行了,这是最简单的一种状态。
if goal in start: return [start]
如果这个目标没有在初始状态下, 我们在定义一个set,这个是表示我们所有探测过的点。
explored = set()
然后,我们还有一个paths, 这个paths就是我们现在已经观测到的所有的点,已经观测到的所有路线。现在有一个start状态,然后要去给他扩展很多路径。
paths = [['init', start]]
现在就定义一个变量paths,这个paths就是指各种各样的路径,但现在只有一条路,现在只知道一个初始节点,这个初始节点就是我们的start。
那么有了这个之后, 我们发现还有路径需要去扩展,咱们现在就取出来这个路径,在这些所有的路线里面取出来一条路。
这条路最后的状态就是这条路的末端,表示的是此时此刻的状态
大家想象一下这个探索的过程,这个路假如已经探索了很多次了,采取了最前面这条路,这条路里面的-1就是现在的这个状态。
while paths:
path = paths.pop(0)
(x, y) = path[-1][-1]
x和y现在是把最末端的状态拿出来了。这个时候,我们刚刚写的函数就有用了:
for state, action in successors(x, y, capacity1, capacity2).items():
pass
我们有了此时此刻的(x,y), 还知道这个杯子的capacity,这段代码就让我们知道最末端的(x, y)接下来的状态了。
那么,如果state在explored中,这个点我们已经探索过了,那么就continue。
if state in explored: continue
如果不这样做,则可能造成前面探索过的点包含下一步的状态中,就会造成形成一个环,从而无限循环。所以我们要把每一个探索过的点加到explored里边。这样我们才可以不兜圈子。
explored.add((x,y))
如果它在explored里边我们就跳过这个循环。它不在这个里边,我们就先定义一个新的path: new_path, 这个新的path就等于之前的老的path再加上action。
new_path = path + [(action, state)]
这个action和state,就是我们刚刚写的那个求接下来的这个action和state。
那现在,如果我们的目标在state里边, 我们就把现在这个new_path给它返回出来。如果不在, 那这个paths里边,探索路线里面, 就再给它加上一个现在的这个路线。
if goal in state:
return new_path
else:
paths.append(new_path)
最后返回一个空, 就说没有这个路径。
这个问题乍一看要用计算机编程的方法去解决会觉得比较复杂,但是我们写完整个也就这么多:
def search_solution(capacity1, capacity2, goal, start=(0,0)):
if goal in start: return [start]
explored = set()
paths = [[('init', start)]]
while paths:
path = paths.pop(0)
(x, y) = path[-1][-1]
for (state, action) in successors(x, y, capacity1, capacity2).items():
if state in explored: continue
new_path = path + [(action, state)]
if goal in state:
return new_path
else:
paths.append(new_path)
explored.add(state)
return []
下面呢,我们来求解一下。 假如我们定义两个杯子, 第一个杯子是9,第二个杯子是4,我们的目标刚开始是5,start是空的。来看看我们该怎么解决:
if __name__ == '__main__':
print(search_solution(9,4,5))
---
[('init', (0, 0)), ('装满x', (9, 0)), ('x => y', (5, 4))]
我们来修改一下这一段代码,让其看着跟清晰一点,我们将步骤和结果分别取出来并且进行打印:
solutin = search_solution(9, 4, 5)
for i, s in enumerate(solution):
print('step:{},{}'.format(i,s))
---
step:0,('init', (0, 0))
step:1,('装满x', (9, 0))
step:2,('x => y', (5, 4))
step0刚开始是(0,0),然后第一步装满x,第二步把x倒给y,把y装满。因为我们知道y是4,所以就可以得到容量是5的水。
那我们现在再来看一下,如果我们现在把这个问题再换一下,我们还是一样(9,4),假如求解是6,如果无解的话会返回一个空,不过最终我们还是得到了解,虽然步骤比较多。
solution = search_solution(9, 4, 6)
---
step:0,('init', (0, 0))
step:1,('装满x', (9, 0))
step:2,('x => y', (5, 4))
step:3,('倒空y', (5, 0))
step:4,('x => y', (1, 4))
step:5,('倒空y', (1, 0))
step:6,('x => y', (0, 1))
step:7,('装满x', (9, 1))
step:8,('x => y', (6, 4))
那我们每次要求一个新解,都需要重新定义一遍solution,这样十分不方便,那我们现在就需要将其修改成一个函数,方便我们随意传入不同的值:
def get_solution(c1, c2, goal, start=(0, 0)):
solution = search_solution(c1, c2, goal, start)
for i, s in enumerate(solution):
print('step:{},{}'.format(i,s))
接着,我们如果求一个.5,就返回一个空。
get_solution(9, 4, 6.5)
返回空的就就是没有路径。
我们再回过头看看刚才的求解(9, 4, 6), 这个时候已经能够解决这个问题了。它不是经过了复杂的数学运算得出来的,是自己找到的结果。那完整的代码如下:
def successors(x, y, X, Y):
return{
(x, 0): '倒空y',
(0, y): '倒空x',
(x, Y): '装满y',
(X, y): '装满x',
(0, x+y) if x+y <= Y else (x+y-Y, Y): 'x => y',
(x+y, 0) if x+y <= X else (X, x+y-x): 'y => x',
}
def search_solution(capacity1, capacity2, goal, start=(0,0)):
if goal in start: return [start]
explored = set()
paths = [[('init', start)]]
while paths:
path = paths.pop(0)
(x, y) = path[-1][-1]
for (state, action) in successors(x, y, capacity1, capacity2).items():
if state in explored: continue
new_path = path + [(action, state)]
if goal in state:
return new_path
else:
paths.append(new_path)
explored.add(state)
return []
def get_solution(c1, c2, goal, start=(0, 0)):
solution = search_solution(c1, c2, goal, start)
for i, s in enumerate(solution):
print('step:{},{}'.format(i,s))
if __name__ == '__main__':
get_solution(9, 4, 6.5)
就这段代码,虽然并不长,但是难度稍微有点大,你们在看完之后最好是多敲几遍。
这就是人们当时讨论AI程序的作用,人们不希望每次都自己去解决,希望能够让程序解决。
我们来试试7:
get_solution(9, 4, 7)
---
step:0,('init', (0, 0))
step:1,('装满x', (9, 0))
step:2,('x => y', (5, 4))
step:3,('倒空y', (5, 0))
step:4,('x => y', (1, 4))
step:5,('倒空y', (1, 0))
step:6,('x => y', (0, 1))
step:7,('装满x', (9, 1))
step:8,('x => y', (6, 4))
step:9,('倒空y', (6, 0))
step:10,('x => y', (2, 4))
step:11,('倒空y', (2, 0))
step:12,('x => y', (0, 2))
step:13,('装满x', (9, 2))
step:14,('x => y', (7, 4))
7也是可以的, 给一个9的杯子和一个4的杯子,要得到7升水也是可以的。只不过过程比较复杂,那如果现在给你人工来解,你觉得7你可以吗?
假如要让你的最短路径优先,你可以在paths.append(new_path)这里做一些优化,就是减枝、排序等等。
7这个问题乍一看感觉是不行的,完不成。但是这倒腾来倒腾去竟然可以,好神奇对不对?
回头我给大家说一个比较容易误解的地方:
(x, y) = path[-1][-1]
就这段代码解释一下, 这个[-1]是你找到一条路径的最后一个节点,并不是值为-1, 因为我们最后一个节点存了两个东西,一个是他的action, 一个是他的状态。所以这个就是他最后那个节点的状态。
这个问题的特点在于咱们从始至终都没有去写数学方程或者找规律,然后求解,而是让程序自动解决的。
同样问题,像刚才传教士和食人族过河,还有那个手电筒、下棋的问题。其实你会发现都是类似的问题。
从研究对象来讲
接着,我们再从最后一个维度上来区分一下人工智能的这个问题,它有什么区别。
从他研究的对象上来看,首先,会有一群人在研究我们怎么样能够创建解决AI的问题和方法,就是研究如何创建能够解决AI问题的方法与模型。


有一部分人是创造模型和方法的人,但还有一些是研究如何使用这些模型和方法的人。

那以上两者,这些人都是AI工作者。有些同学可能是发明算法的,有些同学可能是使用算法的。
因为用现有的方法去解决问题,其实也是很难的一个事情。
好,那么本节课就到这里,这节课还是有一些难度的,希望大家能好好的消化一边,课内代码多敲几遍去理解。
下节课就没这么难了,也就吹吹牛逼聊聊天就过了。不过大家要做好准备,下一节课是咱们最后一节轻松的课程了,之后的课程将会… 大家做好心理准备吧。
好,我是茶桁,咱们下节课见。