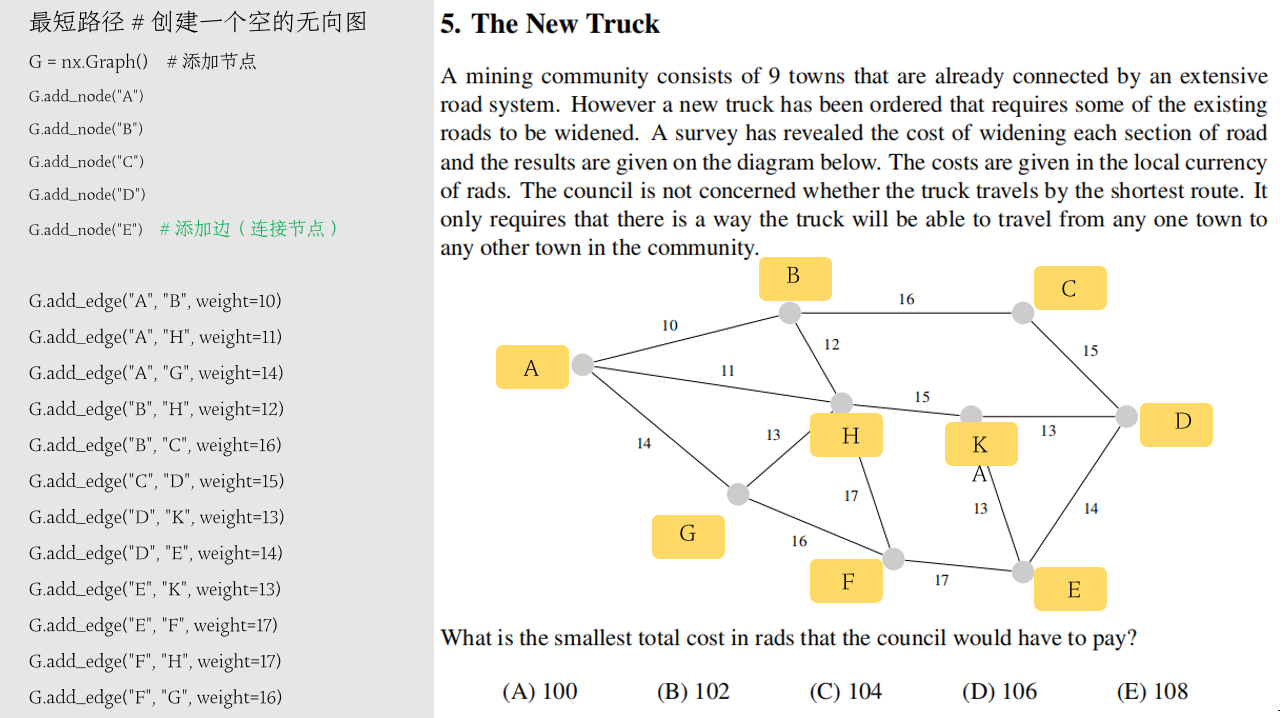
最小生成树 | 市政道路拓宽预算的优化 (Minimum Spanning Tree)

news2024/11/24 4:32:45

任务描述：

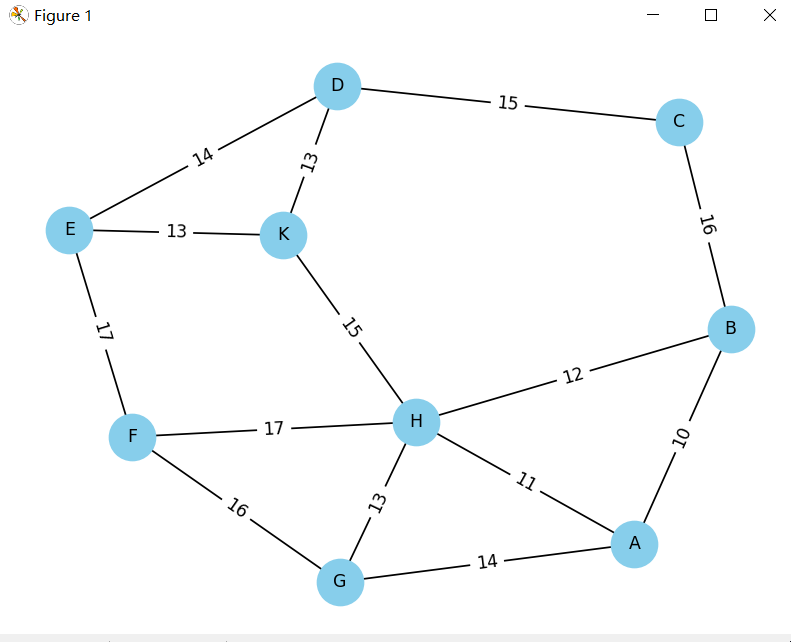
市政投资拓宽市区道路，本着执政为民，节省纳税人钱的目的，论证是否有必要对每一条路都施工拓宽？

这是一个连问带答的好问题。项目制学习可以上下半场，上半场头脑风暴节省投资的所有可行的思路；

下半场总结可行的思路，归为算法问题解决。

思路

MST = Minimum Spanning Tree 最小生成树

1、选择每一个节点的最短边，加入树Tree，涂成颜色标记如下：

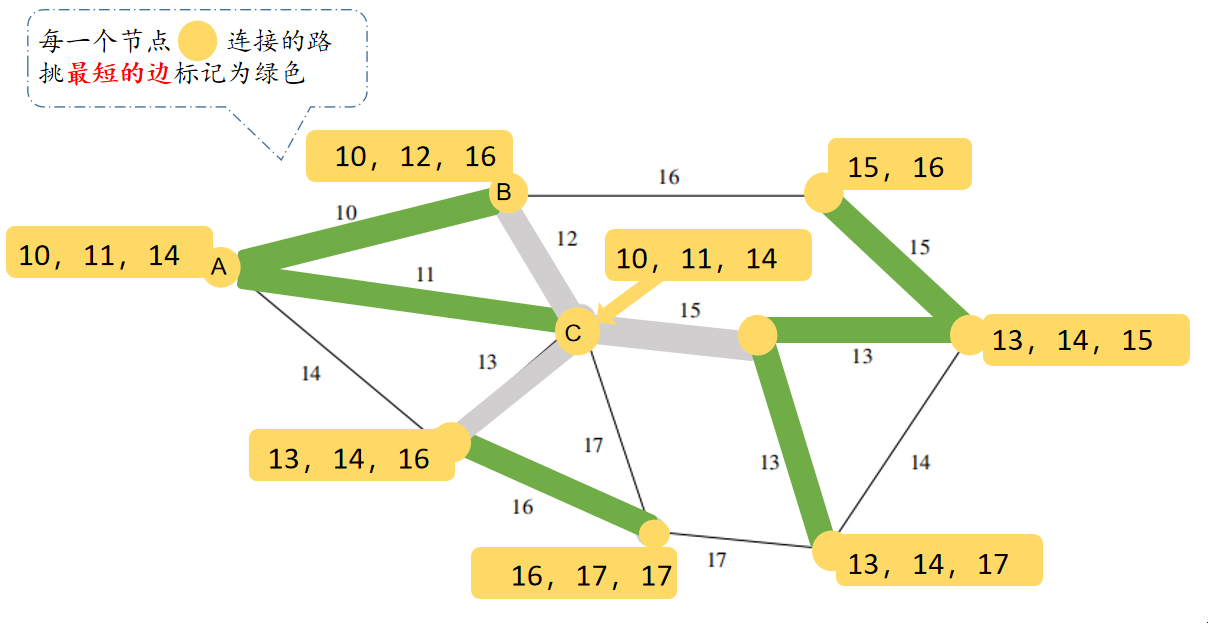
2、同时避免形成环路,

3、遍历所有的节点，循环执行以上步骤直至所有节点都在MST中；

使用Kruskal算法求解最小生成树(Minimum Spanning Tree)的Python代码实现

#上述代码利用Kruskal算法的贪心思想, 每次选择权值最小的边加入MST, 同时避免形成环路,

#直到遍历完所有节点, 得到最小生成树的所有边。

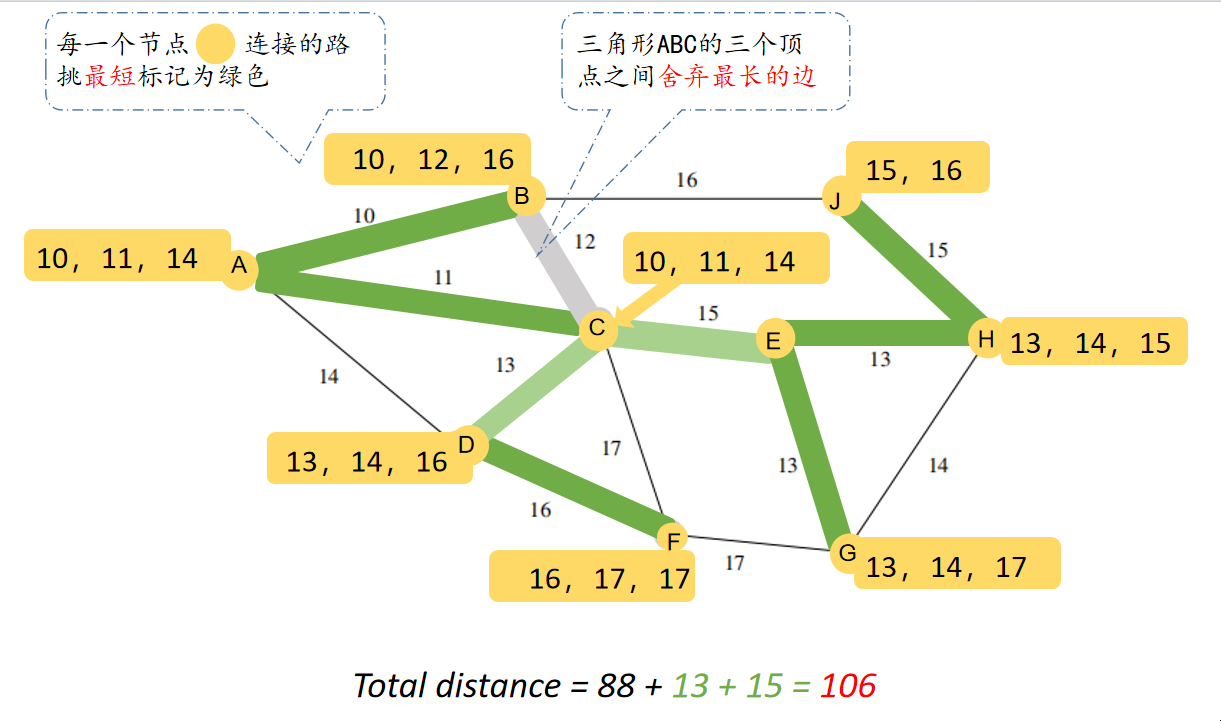
Kruskal算法和Prim算法都是解决最小生成树（Minimum Spanning Tree，MST）问题的常用算法，但它们的工作原理和实现方式略有不同。以下是它们之间的主要区别：

  1. 工作原理：

    • Kruskal算法：Kruskal算法基于贪心策略。它首先将所有的边按权重升序排列，然后从最小权重的边开始，逐渐构建最小生成树。在构建的过程中，Kruskal算法不断选择下一条最小权重的边，但要确保选择的边不会形成环路。它使用了一个并查集（Disjoint Set）数据结构来判断边是否会形成环路。

    • Prim算法：Prim算法也是一种贪心算法，但它从一个初始顶点开始，逐步添加顶点到最小生成树中。它每次选择一个与当前最小生成树相邻的顶点，并选择连接它们的边中权重最小的那条边。这个过程一直进行，直到所有顶点都包含在最小生成树中为止。

  2. 起始点：

    • Kruskal算法：Kruskal算法不需要指定一个起始点，它从边集合出发，根据权重来构建最小生成树。

    • Prim算法：Prim算法需要指定一个起始点，它从指定的起始点开始构建最小生成树。

  3. 数据结构：

    • Kruskal算法：Kruskal算法主要依赖于边的排序和并查集数据结构，用于检测环路。

    • Prim算法：Prim算法通常使用优先队列（Priority Queue）来管理候选边和顶点，以及一个数组来维护顶点的键（键表示连接到最小生成树的最小边的权重）。

  4. 适用情况：

    • Kruskal算法：Kruskal算法适用于稀疏图，即边相对较少的情况。它不受起始点选择的限制，因此在不同起始点下可能会得到相同的最小生成树。

    • Prim算法：Prim算法适用于稠密图，即边相对较多的情况。它的最终结果可能受起始点选择的影响，因为不同的起始点可能会导致不同的最小生成树。

总的来说，Kruskal算法和Prim算法都是有效的最小生成树算法，选择哪个算法取决于具体的问题和图的性质。在实际应用中，可以根据图的密度和其他要求来选择适当的算法。

import sys
class Graph:
    def __init__(self):
        self.graph = {}

    def add_edge(self, u, v, w):
        if u not in self.graph:
            self.graph[u] = {}
        if v not in self.graph:
            self.graph[v] = {}
        self.graph[u][v] = w
        self.graph[v][u] = w

    def prim(self):
        key = {}
        parent = {}
        mst_set = set()

        # 初始化key值为无穷大
        for vertex in self.graph:
            key[vertex] = sys.maxsize
        # 从起始顶点开始
        start_vertex = list(self.graph.keys())[0]
        key[start_vertex] = 0
        parent[start_vertex] = None

        while mst_set != set(self.graph.keys()):
            # 找到key值最小的未加入MST的顶点
            min_vertex = None
            for vertex in self.graph:
                if vertex not in mst_set and (min_vertex is None or key[vertex] < key[min_vertex]):
                    min_vertex = vertex

            mst_set.add(min_vertex)

            # 更新与min_vertex相邻的顶点的key值和parent
            for neighbor, weight in self.graph[min_vertex].items():
                if neighbor not in mst_set and weight < key[neighbor]:
                    key[neighbor] = weight
                    parent[neighbor] = min_vertex

        # 构建最小生成树的边列表
        mst_edges = []
        for vertex, p in parent.items():
            if p is not None:
                mst_edges.append((p, vertex, key[vertex]))

        return mst_edges
创建图并添加边
g = Graph()
g.add_edge("A", "B", 10)
g.add_edge("A", "H", 11)
g.add_edge("A", "G", 14)
g.add_edge("B", "H", 12)
g.add_edge("B", "C", 16)
g.add_edge("C", "D", 15)
g.add_edge("D", "K", 13)
g.add_edge("D", "E", 14)
g.add_edge("E", "K", 13)
g.add_edge("E", "F", 17)
g.add_edge("F", "H", 17)
g.add_edge("F", "G", 16)
g.add_edge("G", "H", 13)
g.add_edge("H", "K", 15)
计算最小生成树
mst = g.prim()

# 打印最小生成树的边和权重
s = 0
for u, v, w in mst:
    s += w
    print(f"{u} - {v}: {w}")
print('total = ',s)

A - B: 10
A - H: 11
H - G: 13
D - C: 15
G - F: 16
H - K: 15
K - D: 13
K - E: 13

total =  106

根据图的疏密程度选择合适的最小生成树算法是一个重要的考虑因素。下面是对于不同的图疏密程度如何选择算法的一些建议：

  1. 稀疏图（Sparse Graph）：

    • Kruskal算法：对于稀疏图，通常边的数量相对较少，这使得Kruskal算法的效率较高。因为Kruskal算法不依赖于起始点，适合用于连接各个部分的边比较少的情况。如果图是非连通的，Kruskal算法也可以应对。

    • Prim算法：虽然Prim算法也可以用于稀疏图，但在这种情况下，通常Kruskal算法更具优势，因为它的时间复杂度相对较低。

  2. 稠密图（Dense Graph）：

    • Prim算法：稠密图通常包含大量的边，此时Prim算法更适合，因为它在连接到当前最小生成树的顶点之间选择边的效率更高。Prim算法的时间复杂度在稠密图中通常比Kruskal算法更低。

  3. 图的连通性：

    • Kruskal算法：如果图是非连通的，Kruskal算法可以构建最小生成森林，而不需要将图变为连通的。这在一些应用中可能很有用。

  4. 起始点选择：

    • Kruskal算法：Kruskal算法不受起始点选择的限制，因此在不同的起始点下可能会得到相同的最小生成树。这对于某些问题可能是一个优点。

    • Prim算法：Prim算法需要指定一个起始点，因此选择起始点可能会影响最终的最小生成树结果。在某些情况下，选择不同的起始点可能导致不同的最小生成树。

总的来说，根据图的疏密程度、连通性和起始点选择的灵活性来选择最小生成树算法。通常，如果图较稀疏，可以优先考虑Kruskal算法，如果图较稠密，可以优先考虑Prim算法。然而，具体的应用可能需要根据问题的特点进行权衡和选择。

同学对算法缺乏兴趣或没有时间研究的，最好的选择，也是Python的优势所在，直接导入第三方库。

额外的福利是收获直观可见的无向图，顺便学习一点可视化。

import networkx as nx
import matplotlib.pyplot as plt

#1 创建一个空的无向图
G = nx.Graph()

#2 添加节点
G.add_node("A")
G.add_node("B")
G.add_node("C")
G.add_node("D")
G.add_node("E")    
G.add_node("F")
G.add_node("G")
G.add_node("H")
G.add_node("K")

#根据需求添加边两端连接节点

#3 添加边（连接节点）
G.add_edge("A", "B", weight=10)
G.add_edge("A", "H", weight=11)
G.add_edge("A", "G", weight=14)
G.add_edge("B", "H", weight=12)
G.add_edge("B", "C", weight=16)
G.add_edge("C", "D", weight=15)
G.add_edge("D", "K", weight=13)
G.add_edge("D", "E", weight=14)
G.add_edge("E", "K", weight=13)
G.add_edge("E", "F", weight=17)
G.add_edge("F", "H", weight=17)
G.add_edge("F", "G", weight=16)
G.add_edge("G", "H", weight=13)
G.add_edge("H", "K", weight=15)

# 绘制图形
pos = nx.spring_layout(G)
nx.draw(G, pos, with_labels=True, node_size=700, node_color='skyblue', font_size=10, font_color='black')
labels = nx.get_edge_attributes(G, 'weight')
nx.draw_networkx_edge_labels(G, pos, edge_labels=labels)

# 查找最小生成树
minimum_spanning_tree = nx.minimum_spanning_tree(G)
print("Minimum Spanning Tree Edges:")
s = 0
for edge in minimum_spanning_tree.edges(data=True):
    s += edge[2]['weight']
    print(edge)


# 查找节点之间的最短路径
shortest_path = nx.shortest_path(G, source="A", target="D", weight="weight")
print("Shortest Path from A to D:", shortest_path)

# 计算最短路径长度
shortest_path_length = nx.shortest_path_length(G, source="A", target="D", weight="weight")
print("Shortest Path Length from A to D:", shortest_path_length)


# 查找节点之间的最短路径
shortest_path = nx.shortest_path(G, source="H", target="K", weight="weight")
print("Shortest Path from H to K:", shortest_path)

# 计算最短路径长度
shortest_path_length = nx.shortest_path_length(G, source="H", target="K", weight="weight")
print("Shortest Path Length from H to K:", shortest_path_length)

# Total length of Minimum Spanning Tree Edges

print(''' totals ''')
print(minimum_spanning_tree) #Graph with 9 nodes and 8 edges
print([edge for edge in minimum_spanning_tree])
print('total length = ',s)


# 显示图形
plt.show()

输出结果：

Minimum Spanning Tree Edges:
('A', 'B', {'weight': 10})
('A', 'H', {'weight': 11})
('C', 'D', {'weight': 15})
('D', 'K', {'weight': 13})
('E', 'K', {'weight': 13})
('F', 'G', {'weight': 16})
('G', 'H', {'weight': 13})
('H', 'K', {'weight': 15})


Shortest Path from A to D: ['A', 'H', 'K', 'D']
Shortest Path Length from A to D: 39
Shortest Path from H to K: ['H', 'K']
Shortest Path Length from H to K: 15
 totals 
Graph with 9 nodes and 8 edges
['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'K']
total length =  106

与原题的图等价。

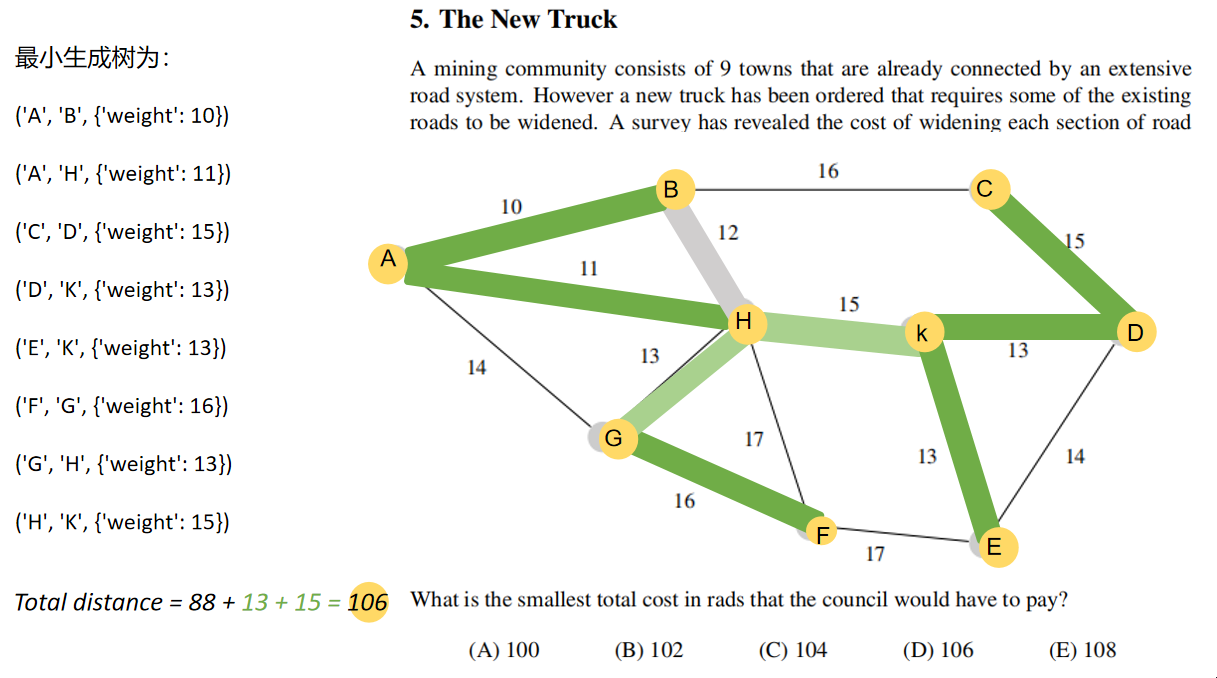
最小生成树为：

('A', 'B', {'weight': 10})

('A', 'H', {'weight': 11})

('C', 'D', {'weight': 15})

('D', 'K', {'weight': 13})

('E', 'K', {'weight': 13})

('F', 'G', {'weight': 16})

('G', 'H', {'weight': 13})

('H', 'K', {'weight': 15})

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1051118.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

因果引擎(Causal Engine)是基于因果推理的人工智能系统

因果引擎(Causal Engine)是基于因果推理的人工智能系统

因果引擎(Causal Engine)是一种基于因果推理的人工智能系统。 其关键思想是通过学习事件之间的因果关系,对环境进行模型化和推理,从而指导AI系统采取行动。 因果引擎的主要特征包括: 建立因果图(Causal Graph):通过统计方法学习不同事件之间的因果关系,构建表示这些因果关系的…
阅读更多...
基于微信小程序的游戏账号交易买卖平台设计与实现(源码+lw+部署文档+讲解等)

基于微信小程序的游戏账号交易买卖平台设计与实现(源码+lw+部署文档+讲解等)

文章目录 前言系统主要功能&#xff1a;具体实现截图论文参考详细视频演示为什么选择我自己的网站自己的小程序&#xff08;小蔡coding&#xff09;有保障的售后福利 代码参考源码获取 前言 &#x1f497;博主介绍&#xff1a;✌全网粉丝10W,CSDN特邀作者、博客专家、CSDN新星计…
阅读更多...
通过 Azure 日志分析加强云安全

通过 Azure 日志分析加强云安全

Microsoft Azure 云服务在安全日志存储、访问、可伸缩性、降低成本和易于部署方面提供了巨大的优势&#xff0c;因此在企业中很受欢迎。 Microsoft Azure 日志记录工具&#xff08;如 Log360&#xff09;可帮助管理 Azure 云基础结构中所有设备和应用程序&#xff08;如虚拟机…
阅读更多...
Linux：nginx---web文件服务器

Linux：nginx---web文件服务器

我这里使用的是centos7系统 nginx源码包安装 Linux&#xff1a;nginx基础搭建&#xff08;源码包&#xff09;_鲍海超-GNUBHCkalitarro的博客-CSDN博客https://blog.csdn.net/w14768855/article/details/131445878?ops_request_misc%257B%2522request%255Fid%2522%253A%25221…
阅读更多...
Spring | 基于SpringBoot的多数据源实战 - 使用seata实现多数据源的全局事务管理

Spring | 基于SpringBoot的多数据源实战 - 使用seata实现多数据源的全局事务管理

Spring | 基于SpringBoot的多数据源实战 - 使用seata实现多数据源的全局事务管理 引言1.1 多数据源的必要性1.2 多数据源的应用场景 实战演示2.1 创建实体类2.2 配置数据源2.3 实现数据源配置类2.4 配置Repository类2.5 运行与验证 事务管理与数据一致性3.1 事务管理3.2 使用Se…
阅读更多...
长假，GPT来敲(Jué)门(Fén)

长假，GPT来敲(Jué)门(Fén)

引 马上十一了&#xff0c;本拐在干了XX和XX事情以后&#xff0c;开始划水&#xff0c;欢天喜地的等放假。 然后&#xff0c;GPT4说更新了&#xff0c;据说加了一个读图的功能&#xff0c;本拐不以为然&#xff0c;不就是什么文生图&#xff0c;图生文么&#xff0c;TOOOLD。 不…
阅读更多...
案例题-系统开发

案例题-系统开发

案例题-系统开发 结构化分析方法概述面向对象分析方法真题1真题2 结构化分析方法概述 面向对象分析方法 了解一下符号就行 依赖关系&#xff1a;一个事务的变化影响另外一个事务的变化 泛化关系&#xff0c;父类子类 聚合&#xff1a;部分和整体之间的生命周期不同 组合&#x…
阅读更多...
Cache系列直播，这次真的来了！

Cache系列直播，这次真的来了！

1、要学cache&#xff0c;一大堆一大堆待讨论的问题。例如近期的一些问题&#xff1a; L1、L2、L3 cache的替换策略是怎样的&#xff1f;什么类型的内存永远不会进L3 cache&#xff1f;L3 cache一般都是多大&#xff1f;L3 cache的组织形式一般是怎样的&#xff1f;什么是cache…
阅读更多...
MySQL体系结构和四层架构介绍

MySQL体系结构和四层架构介绍

MySQL体系结构图如下&#xff1a; 四层介绍 1. 连接层&#xff1a; 它的主要功能是处理客户端与MySQL服务器之间的连接(比如Java应用程序通过JDBC连接MySQL)。当客户端应用程序连接到MySQL服务器时&#xff0c;连接层对用户进行身份验证、建立安全连接并管理会话状态。它还处理…
阅读更多...
医疗图像分割指标

医疗图像分割指标

医疗图像其中两种图像格式&#xff1a;MRI&#xff08;Magnetic Resonance Imaging&#xff0c;磁共振成像&#xff09;、CT&#xff08;Computed Tomography&#xff0c;计算机断层&#xff09;&#xff0c;常存成 .nii.gz 格式。都是 3D 的 H W L H \times W \times L HWL…
阅读更多...
数字孪生智慧能源：风光储一体化能源中心

数字孪生智慧能源：风光储一体化能源中心

自“双碳”目标提出以来&#xff0c;我国能源产业不断朝着清洁低碳化、绿色化的方向发展。其中&#xff0c;风能、太阳能等可再生能源在促进全球能源可持续发展、共建清洁美丽世界中被寄予厚望。风能、太阳能具有波动性、间歇性、随机性等特点&#xff0c;主要通过转化为电能再…
阅读更多...
jvm内存分配与回收策略

jvm内存分配与回收策略

自动内存管理 解决两个问题 自动给对象分配内存 对象一般堆上分配&#xff08;而实际上也有可能经过即时编译后被拆散为标量类型并间接地在栈上分配&#xff09; 新生对象通常会分配在新生代&#xff0c;少数情况下&#xff08;例如对象大小超过一定阈值&#xff09;也可能…
阅读更多...
[H5动画制作系列 ]变量,帧频,监听器等的生命周期基础测试

[H5动画制作系列 ]变量,帧频,监听器等的生命周期基础测试

模式:按照上述抓图,actions层&#xff0c;1帧,写初始化代码,10帧写返回代码到2帧代码,2-10帧之间一直循环。1帧及10帧代码如下&#xff1a; 如果程序在1-10之间循环,会反复创建变量i,多个监听器等。所以,第一帧最好执行一次即可&#xff0c;程序在2-10帧之间一直循环。
阅读更多...
《Upload-Labs》01. Pass 1~13

《Upload-Labs》01. Pass 1~13

Upload-Labs 索引前言Pass-01题解 Pass-02题解总结 Pass-03题解总结 Pass-04题解 Pass-05题解总结 Pass-06题解总结 Pass-07题解总结 Pass-08题解总结 Pass-09题解 Pass-10题解 Pass-11题解 Pass-12题解总结 Pass-13题解 靶场部署在 VMware - Win7。 靶场地址&#xff1a;https…
阅读更多...
Leetcode290. 单词规律

Leetcode290. 单词规律

给定一种规律 pattern 和一个字符串 s &#xff0c;判断 s 是否遵循相同的规律。 这里的 遵循 指完全匹配&#xff0c;例如&#xff0c; pattern 里的每个字母和字符串 s 中的每个非空单词之间存在着双向连接的对应规律。 解题思路&#xff1a;哈希 力扣&#xff08;LeetCode&…
阅读更多...
软件测试中的测试工具和自动化测试

软件测试中的测试工具和自动化测试

1. 测试工具 测试工具也分为不同人员使用的 开发人员&#xff1a;测试框架&#xff0c;编写测试用例&#xff1b;各类线上dump分析工具如windgb&#xff1b;开发时的集成IDE工具如Visual Studio&#xff0c;idea等等 面向不同测试需求的测试工具 软件测试是软件开发生命周期…
阅读更多...
网络子网划分练习

网络子网划分练习

网络子网划分练习 1.背景&#xff1a; 在一个仓储企业网络拓朴结构如图1-所示&#xff0c;该企业占地500亩。有五层办公楼1栋&#xff0c;大型仓库10栋。每栋仓库内、外部配置视频监控16台&#xff0c;共计安装视频监控160台&#xff0c;Switch A、服务器、防火墙、管理机、Rou…
阅读更多...
UE4/5数字人MetaHuman通过已有动画进行修改

UE4/5数字人MetaHuman通过已有动画进行修改

目录 通过已有动画修改动画 开始制作 创建一个关卡序列 将动画序列烘焙到控制绑定 打开我们自己创建的动画序列 之后便是烘焙出来 通过已有动画修改动画 首先架设我们已经有相关的MetaHuman的动画&#xff0c;但是这个动画因为是外部导入进来的&#xff0c;所以可能会出…
阅读更多...
基于微信小程序的刷题考试系统设计与实现(适用于各类考试类、答题类程序)

基于微信小程序的刷题考试系统设计与实现(适用于各类考试类、答题类程序)

文章目录 前言系统主要功能&#xff1a;具体实现截图论文参考详细视频演示为什么选择我自己的网站自己的小程序&#xff08;小蔡coding&#xff09;有保障的售后福利 代码参考源码获取 前言 &#x1f497;博主介绍&#xff1a;✌全网粉丝10W,CSDN特邀作者、博客专家、CSDN新星计…
阅读更多...
C/C++跨平台构建工具CMake入门

C/C++跨平台构建工具CMake入门

文章目录 1.概述2.环境准备2.1 安装编译工具2.2 安装CMake 3.编译一个示例程序总结 1.概述 本人一直对OpenGL的3d渲染很感兴趣&#xff0c;但是苦于自己一直是Android开发&#xff0c;没有机会接触这方面的知识。就在最近吗&#xff0c;机会来了&#xff0c;以前一个做3D渲染的…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023