1 NumPy介绍

NumPy 软件包是Python生态系统中数据分析、机器学习和科学计算的主力军。它极大地简化了向量和矩阵的操作处理。Python的一些主要软件包（如 scikit-learn、SciPy、pandas 和 tensorflow）都以 NumPy 作为其架构的基础部分。除了能对数值数据进行切片（slice）和切块（dice）之外，使用 NumPy 还能为处理和调试上述库中的高级实例带来极大便利，享有数据分析“三剑客之一”的盛名（NumPy、Matplotlib、Pandas）。

1.1 NumPy的主要特点

• 多维数组：NumPy引入了多维数组对象（称为numpy.ndarray或简称为数组），它允许你在单个数据结构中存储和操作多维数据，如向量、矩阵和张量。

• 快速的数值运算：NumPy的底层实现是用C语言编写的，因此它能够执行高效的数值计算。它提供了一系列高度优化的数学函数，可用于执行各种数学和统计操作。

• 强大的索引和切片：NumPy提供了丰富的索引和切片功能，允许你高效地访问和操作数组的元素。

• 丰富的数学函数库：NumPy包含了大量的数学函数，用于执行各种数值计算，如三角函数、指数函数、对数函数等。NumPy包含了线性代数操作的函数，如矩阵乘法、特征值分解、奇异值分解等，使其成为数值线性代数的强大工具。

• 互操作性：NumPy与其他常用的科学计算库（如SciPy、pandas和Matplotlib）紧密集成，使得在不同库之间传递数据变得非常容易。

1.2 NumPy数据类型

NumPy支持的数据类型比 Python 内置的类型要多很多，基本上可以和 C 语言的数据类型对应上，其中部分类型对应为 Python 内置的类型。下表列举了常用 NumPy 基本类型。

名称	描述
bool_	布尔型数据类型（True 或者 False）
int_	默认的整数类型（类似于 C 语言中的 long，int32 或 int64）
intc	与 C 的 int 类型一样，一般是 int32 或 int 64
intp	用于索引的整数类型（类似于 C 的 ssize_t，一般情况下仍然是 int32 或 int64）
int8	字节（-128 to 127）
int16	整数（-32768 to 32767）
int32	整数（-2147483648 to 2147483647）
int64	整数（-9223372036854775808 to 9223372036854775807）
uint8	无符号整数（0 to 255）
uint16	无符号整数（0 to 65535）
uint32	无符号整数（0 to 4294967295）
uint64	无符号整数（0 to 18446744073709551615）
float_	float64 类型的简写
float16	半精度浮点数，包括：1 个符号位，5 个指数位，10 个尾数位
float32	单精度浮点数，包括：1 个符号位，8 个指数位，23 个尾数位
float64	双精度浮点数，包括：1 个符号位，11 个指数位，52 个尾数位
complex_	complex128 类型的简写，即 128 位复数
complex64	复数，表示双 32 位浮点数（实数部分和虚数部分）
complex128	复数，表示双 64 位浮点数（实数部分和虚数部分）

numpy的数值类型实际上是dtype对象的实例，并对应唯一的字符，包括np.bool_，np.int32，np.float32等等。

数据类型对象 (dtype)

数据类型对象（numpy.dtype 类的实例）用来描述与数组对应的内存区域是如何使用，它描述了数据的以下几个方面：：

• 数据的类型（整数，浮点数或者 Python 对象）
• 数据的大小（例如， 整数使用多少个字节存储）
• 数据的字节顺序（小端法或大端法）
• 在结构化类型的情况下，字段的名称、每个字段的数据类型和每个字段所取的内存块的部分
• 如果数据类型是子数组，那么它的形状和数据类型是什么。

字节顺序是通过对数据类型预先设定“<”或“>”来决定的。

• “<”意味着小端法(最小值存储在最小的地址，即低位组放在最前面)。
• “>”意味着大端法(最重要的字节存储在最小的地址，即高位组放在最前面)。

dtype 对象是使用以下语法构造的：

numpy.dtype(object, align, copy)

• object - 要转换为的数据类型对象
• align - 如果为 true，填充字段使其类似C的结构体。
• copy - 复制 dtype 对象 ，如果为false，则是对内置数据类型对象的引用

1.3 ndarray对象

NumPy最重要的一个特点是其N维数组对象ndarray，它是一系列同类型数据的集合，以0下标为开始进行集合中元素的索引。
（1）ndarray对象是用于存放同类型元素的多维数组。
（2）ndarray中的每个元素在内存中都有相同存储大小的区域。
（3）ndarray内部由以下内容组成：

• 一个指向数据（内存或内存映射文件中的一块数据）的指针。
• 数据类型或dtype，描述在数组中的固定大小值的格子。
• 一个表示数组形状（shape）的元组，表示各维度大小的元组。

NumPy的数组中比较重要ndarray对象属性有：

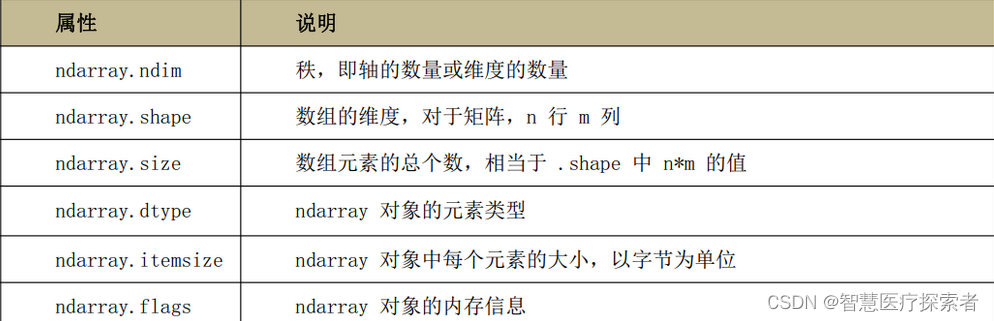
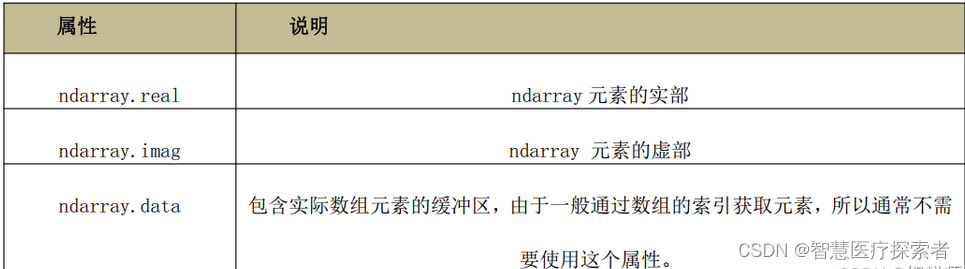
 2 NumPy的使用

2.1 创建数组

我们可以通过传递一个 python 列表并使用 np.array（）来创建 NumPy 数组（可以是一维或多为数组）：

import numpy as np

na1 = np.array([1, 2, 3])
na2 = np.array([[1, 2, 3], [4, 5, 6]])

print('na1:', type(na1), na1)
print('na2:', type(na2), na2)

运行结果显示如下：

na1: <class 'numpy.ndarray'> [1 2 3]
na2: <class 'numpy.ndarray'> [[1 2 3]
 [4 5 6]]

通常我们希望NumPy 能初始化数组的值，为此NumPy提供了ones()、zeros() 和 random.random() 等方法。我们只需传递希望 NumPy 生成的元素数量即可：

import numpy as np

na3 = np.ones(3)
na4 = np.zeros(3)
na5 = np.random.random(3)
print('na3:', type(na3), na3)
print('na4:', type(na4), na4)
print('na5:', type(na5), na5)

运行结果显示如下：

na3: <class 'numpy.ndarray'> [1. 1. 1.]
na4: <class 'numpy.ndarray'> [0. 0. 0.]
na5: <class 'numpy.ndarray'> [0.69669951 0.86211956 0.37149526]

2.2 数组的算术运算

若要计算两个数组的加法，只需要+号操作，就可以实现对应位置上的数据相加的操作（即每行数据进行相加），这种操作比循环读取数组的方法代码实现更加简洁。

import numpy as np

na6 = np.array([[1, 2, 3], [4, 5, 6]])
na7 = np.ones((2, 3))
na8 = na6 + na7
print('na6:', type(na6), na6)
print('na7:', type(na7), na7)
print('na8:', type(na8), na8)

运行结果显示：

na6: <class 'numpy.ndarray'> [[1 2 3]
 [4 5 6]]
na7: <class 'numpy.ndarray'> [[1. 1. 1.]
 [1. 1. 1.]]
na8: <class 'numpy.ndarray'> [[2. 3. 4.]
 [5. 6. 7.]]

减法、乘法和除法等操作与加法一致

import numpy as np

na9 = np.array([[1, 2, 3], [4, 5, 6]])
na10 = np.array([[1, 2, 3], [4, 5, 6]])
na11 = na10 - na9
na12 = na10 * na9
na13 = na10 / na9

print('na9:', type(na9), na9)
print('na10:', type(na10), na10)
print('na11:', type(na11), na11)
print('na12:', type(na12), na12)
print('na13:', type(na13), na13)

运行结果显示如下：

na9: <class 'numpy.ndarray'> [[1 2 3]
 [4 5 6]]
na10: <class 'numpy.ndarray'> [[1 2 3]
 [4 5 6]]
na11: <class 'numpy.ndarray'> [[0 0 0]
 [0 0 0]]
na12: <class 'numpy.ndarray'> [[ 1  4  9]
 [16 25 36]]
na13: <class 'numpy.ndarray'> [[1. 1. 1.]
 [1. 1. 1.]]

许多情况下，我们希望进行数组和单个数值的操作（也称作向量和标量之间的操作）。NumPy通过数组广播（broadcasting）知道这种操作需要和数组的每个元素相乘。

import numpy as np

na14 = np.array([[1, 2, 3], [4, 5, 6]])
na15 = na14 * 3
print('na14:', type(na14), na6)
print('na15:', type(na15), na15)

运行结果显示如下：

na14: <class 'numpy.ndarray'> [[1 2 3]
 [4 5 6]]
na15: <class 'numpy.ndarray'> [[ 3  6  9]
 [12 15 18]]

2.3 数组的切片操作

我们可以像python列表操作那样对NumPy数组进行索引和切片，如下图所示：

import numpy as np

na16 = np.array([[1, 2, 3], [4, 5, 6]])
na17 = na16[0]
na18 = na16[:, 0:2]
na19 = na16[:, :1]
na20 = na16[:, 1:]

print('na16:', type(na16), na16)
print('na17:', type(na17), na17)
print('na18:', type(na18), na18)
print('na19:', type(na19), na19)
print('na20:', type(na20), na20)

运行结果显示如下：

na15: <class 'numpy.ndarray'> [[ 3  6  9]
 [12 15 18]]
na16: <class 'numpy.ndarray'> [[1 2 3]
 [4 5 6]]
na17: <class 'numpy.ndarray'> [1 2 3]
na18: <class 'numpy.ndarray'> [[1 2]
 [4 5]]
na19: <class 'numpy.ndarray'> [[1]
 [4]]
na20: <class 'numpy.ndarray'> [[2 3]
 [5 6]]

2.4 聚合函数

NumPy的聚合函数可以将数据进行压缩，统计数组中的一些特征值：

import numpy as np

na21 = np.array([[1, 2, 3], [4, 5, 6]])
print('na21:', type(na21), na21)
print('na21.max:', na21.max())
print('na21.min:', na21.min())
print('na21.sum:', na21.sum())

运行代码显示结果如下：

na21: <class 'numpy.ndarray'> [[1 2 3]
 [4 5 6]]
na21.max: 6
na21.min: 1
na21.sum: 21

除了min，max和sum等函数，还有mean（均值），prod（数据乘法）计算所有元素的乘积，std（标准差）等等。NumPy能够所有函数应用到任意维度上。

2.5 数组的转置

处理矩阵时经常需要对矩阵进行转置操作，常见的情况如计算两个矩阵的点积。NumPy数组的属性T可用于获取矩阵的转置。

import numpy as np

na22 = np.array([[1, 2, 3], [4, 5, 6]])
na23 = na22.T
print('na22:', type(na22), na22)
print('na23:', type(na23), na23)

运行结果显示如下：

na22: <class 'numpy.ndarray'> [[1 2 3]
 [4 5 6]]
na23: <class 'numpy.ndarray'> [[1 4]
 [2 5]
 [3 6]]

2.6 数组的维度变换

在较为复杂的用例中，改变某个矩阵的维度在机器学习应用中很常见，例如模型的输入矩阵形状与数据集不同，可以使用NumPy的reshape()方法。只需将矩阵所需的新维度传入即可。也可以传入-1，NumPy可以根据你的矩阵推断出正确的维度：

import numpy as np

na24 = np.array([[1, 2, 3], [4, 5, 6]])
na25 = na24.reshape(-1)
na26 = na24.reshape(3, -1)

print('na24:', type(na24), na24)
print('na25:', type(na25), na25)
print('na26:', type(na26), na26)

运行结果显示如下：

na24: <class 'numpy.ndarray'> [[1 2 3]
 [4 5 6]]
na25: <class 'numpy.ndarray'> [1 2 3 4 5 6]
na26: <class 'numpy.ndarray'> [[1 2]
 [3 4]
 [5 6]]

2.7 串联数组

在Numpy中，连接或连接两个数组主要通过以下例程完成:

• np.concatenate ()
• np.vstack ()
• np.hstack ()

hstack()是横向拉伸，vstack()是纵向排列

import numpy as np

a = np.array([1, 2, 3])
b = np.array([4, 5, 6])
print('np.concatenate:', np.concatenate([a, b]))
print('np.stack:', np.stack((a, b)))
print('np.hstack:', np.hstack((a, b)))
print('np.vstack:', np.vstack((a, b)))

运行代码显示如下：

np.concatenate: [1 2 3 4 5 6]
np.stack: [[1 2 3]
 [4 5 6]]
np.hstack: [1 2 3 4 5 6]
np.vstack: [[1 2 3]
 [4 5 6]]

2.8 创建数组的副本

为了防止原数据被更改，我们需要使用数组的副本进行修改

import numpy as np

n1 = np.array([1, 2, 3, 4, 5, 6])
n2 = n1.copy()
n2[2] = 16

print('n1,', n1)
print('n2,', n2)

运行结果显示如下：

n1, [1 2 3 4 5 6]
n2, [ 1  2 16  4  5  6]

当使用了copy函数之后，原先数组的内容没有被改变 

2.9 生成随机数

函数名                                   说明
seed([seed])                          设定随机种子，这样每次生成的随机数会相同
rand(d0,d1,d2.....)                   返回数据在[0,1)之间，具有均匀分布
randn(d0,d1,d2....)                   返回标准正态分布(均值0，方差1)
randint(low[,high,size,dtype])        返回随机整数，包含low，不包含high
choice(a[,size,replace,p])            a是一个数组，从它之间生成随机结果
random([size])                        随机生成[0.0,1.0)之间的小数
shuffle(x)                            把数组x进行随机排列
permutation(x)                        把数组x进行随机排列，或数字的全排列
normal（[loc，scale，size]）           按照平均值loc和方差scale生成高斯分布的数字
uniform([loc,high,size])              在[loc,high)之间生成均匀分布的数字    

示例代码如下：

from numpy import random

# 设定随机数种子
random.seed(134)

# 产生均匀分布的随机数，维度是 3*2
rd1 = random.rand(3, 2)

# 产生标准正态分布随机数，维度是3*2
rd2 = random.randn(3, 2)

# 在[0,1）内产生随机数，维度是3*2
rd3 = random.random((3, 2))

# 产生指定区间的随机整数，维度是3*2
rd4 = random.randint(low=2, high=10, size=(3, 2))

# 正态分布，loc表示均值，scale表示方差
rd5 = random.normal(loc=0, scale=1, size=(3, 2))

# 泊松分布
rd6 = random.poisson(lam=100, size=(3, 2))

# 均匀分布
rd7 = random.uniform(low=3, high=10, size=(3, 2))

# 产生beta分布
rd8 = random.beta(a=3, b=5, size=(3, 2))

# 二项分布（伯努利分布）
rd9 = random.binomial(n=4, p=0.8, size=(3, 2))

# 指数分布
rd10 = random.exponential(scale=3, size=(3, 2))

# F分布
rd11 = random.f(dfnum=100, dfden=5, size=(3, 2))

print('rd1:均匀分布随机数,', type(rd1), rd1)
print('rd2:标准正态分布随机数,', type(rd2), rd2)
print('rd3:[0,1）内随机数,', type(rd3), rd3)
print('rd4:指定区间随机整数,', type(rd4), rd4)
print('rd5:正态分布随机数,', type(rd5), rd5)
print('rd6:泊松分布随机数,', type(rd6), rd6)
print('rd7:均匀分布随机数,', type(rd7), rd7)
print('rd8:beta分布随机数,', type(rd8), rd8)
print('rd9:二项分布随机数,', type(rd9), rd9)
print('rd10:指数分布随机数,', type(rd10), rd10)
print('rd11:F分布随机数,', type(rd11), rd11)

代码运行结果如下：

rd1:均匀分布随机数, <class 'numpy.ndarray'> [[0.81140363 0.44776424]
 [0.62774566 0.88189881]
 [0.66507475 0.88336659]]
rd2:标准正态分布随机数, <class 'numpy.ndarray'> [[ 0.97039702  1.24282664]
 [-0.67460194 -0.84406944]
 [ 0.93530265 -0.61157504]]
rd3:[0,1）内随机数, <class 'numpy.ndarray'> [[0.25060872 0.42907009]
 [0.1313138  0.89065944]
 [0.82592591 0.83688403]]
rd4:指定区间随机整数, <class 'numpy.ndarray'> [[8 5]
 [9 6]
 [2 2]]
rd5:正态分布随机数, <class 'numpy.ndarray'> [[ 1.100513   -0.42039106]
 [-1.10360106  0.02232551]
 [ 0.32110961 -0.36777648]]
rd6:泊松分布随机数, <class 'numpy.ndarray'> [[107 115]
 [115 103]
 [106  96]]
rd7:均匀分布随机数, <class 'numpy.ndarray'> [[9.89957515 7.41625103]
 [8.93349957 8.06628742]
 [5.32215763 9.38106301]]
rd8:beta分布随机数, <class 'numpy.ndarray'> [[0.2429263  0.27533795]
 [0.41979653 0.35869193]
 [0.28791419 0.58321106]]
rd9:二项分布随机数, <class 'numpy.ndarray'> [[3 4]
 [3 3]
 [2 3]]
rd10:指数分布随机数, <class 'numpy.ndarray'> [[ 4.0339984  17.68071959]
 [ 4.47291717  0.35065901]
 [ 1.85350233  4.68708558]]
rd11:F分布随机数, <class 'numpy.ndarray'> [[1.8011784  2.64674957]
 [0.84790891 3.0107673 ]
 [1.17835139 0.80522586]]

2.10 排序、条件筛选函数

NumPy 提供了多种排序的方法。 这些排序函数实现不同的排序算法，每个排序算法的特征在于执行速度，最坏情况性能，所需的工作空间和算法的稳定性。 下表显示了三种排序算法的比较。

种类	速度	最坏情况	工作空间	稳定性
'quicksort'（快速排序）	1	O(n^2)	0	否
'mergesort'（归并排序）	2	O(n*log(n))	~n/2	是
'heapsort'（堆排序）	3	O(n*log(n))	0	否

numpy.sort() 函数返回输入数组的排序副本。函数格式如下：

numpy.sort(a, axis, kind, order)

参数说明：

• a: 要排序的数组
• axis: 沿着它排序数组的轴，如果没有数组会被展开，沿着最后的轴排序， axis=0 按列排序，axis=1 按行排序
• kind: 默认为'quicksort'（快速排序）
• order: 如果数组包含字段，则是要排序的字段

 示例代码如下：

import numpy as np

np1 = np.array([[1, 2, 3], [4, 5, 6]])
print('np1,', np.sort(a))
print('np1 sort,', np.sort(a))
print('np1 sort(a, axis=0),', np.sort(a, axis=0))
dt = np.dtype([('name', 'S10'), ('age', int)])
np2 = np.array([("raju", 21), ("anil", 25), ("ravi", 17), ("amar", 27)], dtype=dt)
print('np2,', np2)
print('np2 sort,', np.sort(np2, order='name'))

 运行结果显示如下：

np1, [1 2 3]
np1 sort, [1 2 3]
np1 sort(a, axis=0), [1 2 3]
np2, [(b'raju', 21) (b'anil', 25) (b'ravi', 17) (b'amar', 27)]
np2 sort, [(b'amar', 27) (b'anil', 25) (b'raju', 21) (b'ravi', 17)]

numpy.argsort() 函数返回的是数组值从小到大的索引值。示例代码如下：

import numpy as np

np3 = np.array([3, 1, 2])
idx = np.argsort(np3)
print('np3,', np3)
print('np.argsort,', idx)
print('以排序后的顺序重构原数组：', np3[idx])

 运行结果显示：

np3, [3 1 2]
np.argsort, [1 2 0]
以排序后的顺序重构原数组： [1 2 3]

numpy.lexsort() 用于对多个序列进行排序。把它想象成对电子表格进行排序，每一列代表一个序列，排序时优先照顾靠后的列。

这里举一个应用场景：小升初考试，重点班录取学生按照总成绩录取。在总成绩相同时，数学成绩高的优先录取，在总成绩和数学成绩都相同时，按照英语成绩录取。这里，总成绩排在电子表格的最后一列，数学成绩在倒数第二列，英语成绩在倒数第三列。

import numpy as np

nm = ('raju', 'anil', 'ravi', 'amar')
dv = ('f.y.', 's.y.', 's.y.', 'f.y.')
ind = np.lexsort((dv, nm))
print('lexsort处理后：', ind)
print('使用这个索引来获取排序后的数据：', [nm[i] + ", " + dv[i] for i in ind])

运行结果显示如下：

以排序后的顺序重构原数组： [1 2 3]
lexsort处理后： [3 1 0 2]
使用这个索引来获取排序后的数据： ['amar, f.y.', 'anil, s.y.', 'raju, f.y.', 'ravi, s.y.']

numpy.where() 函数返回输入数组中满足给定条件的元素的索引。

import numpy as np

np4 = np.arange(9.).reshape(3,  3)
print('np4：', np4)
print('大于3的元素的索引：')
np5 = np.where(np4 > 3)
print(np5)
print('使用这些索引来获取满足条件的元素：')
print(np4[np5])

 运行结果显示如下：

np4： [[0. 1. 2.]
 [3. 4. 5.]
 [6. 7. 8.]]
大于3的元素的索引：
(array([1, 1, 2, 2, 2], dtype=int64), array([1, 2, 0, 1, 2], dtype=int64))
使用这些索引来获取满足条件的元素：
[4. 5. 6. 7. 8.]

2.11 公式应用

NumPy的关键用例是实现适用于矩阵和向量的数学公式。这也Python中常用NumPy的原因。例如，均方误差是监督机器学习模型处理回归问题的核心：

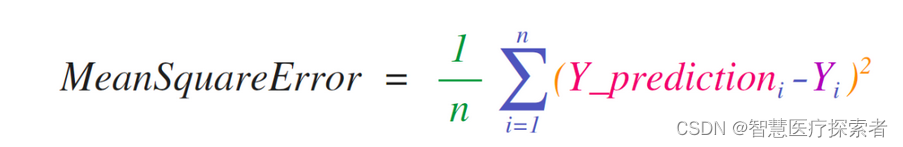
在NumPy中可以很容易地实现均方误差：

这样做的好处是，numpy无需考虑predictions与labels具体包含的值，代码示例如下：

import numpy as np

predictions = np.array([1, 1, 1])
lables = np.array([1, 2, 3])
error = (1/3) * np.sum(np.square(predictions - lables))

print('error:', error)

运行结果显示如下：

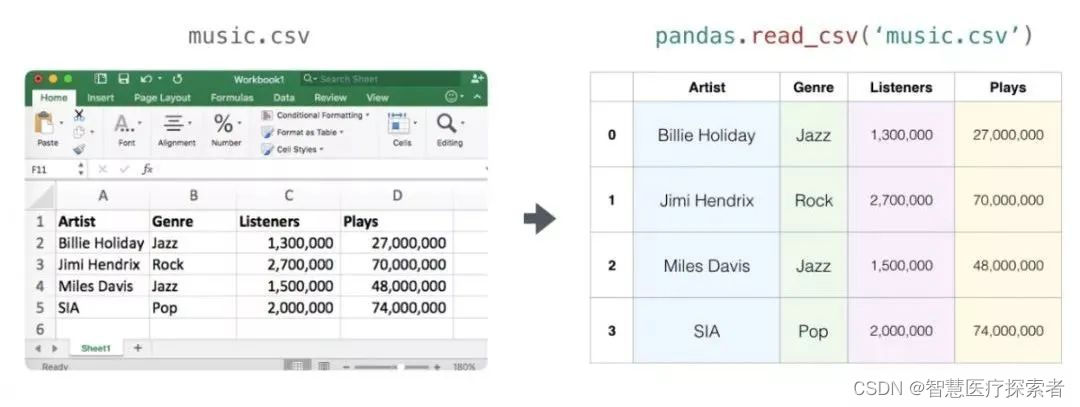
error: 1.6666666666666665

2.12 表和电子表格

电子表格或数据表都是二维矩阵。电子表格中的每个工作表都可以是自己的变量。python中类似的结构是pandas数据帧（dataframe），它实际上使用NumPy来构建的。

2.13 音频和时间序列

音频文件是一维样本数组。每个样本都是代表一小段音频信号的数字。CD质量的音频每秒可能有44,100个采样样本，每个样本是一个-65535到65536之间的整数。这意味着如果你有一个10秒的CD质量的WAVE文件，你可以将它加载到长度为10 * 44,100 = 441,000个样本的NumPy数组中。想要提取音频的第一秒？只需将文件加载到我们称之为audio的NumPy数组中，然后截取audio[:44100]。

以下是一段音频文件：

时间序列数据也是如此（例如，股票价格随时间变化的序列）。

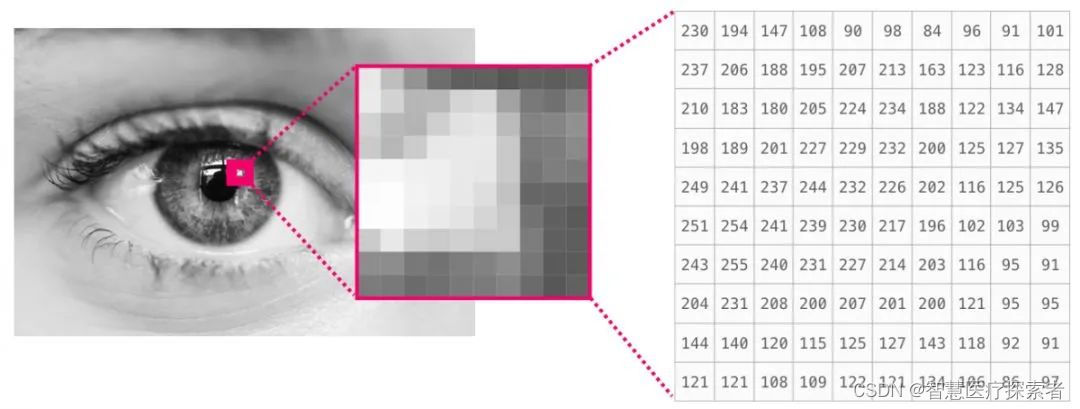
2.14 图像数据

图像是大小为（高度×宽度）的像素矩阵。如果图像是黑白图像（也称为灰度图像），则每个像素可以由单个数字表示（通常在0（黑色）和255（白色）之间）。如果对图像做处理，裁剪图像的左上角10 x 10大小的一块像素区域，用NumPy中的image[:10,:10]就可以实现。

这是一个图像文件的片段：

如果图像是彩色的，则每个像素由三个数字表示 ：红色，绿色和蓝色。在这种情况下，我们需要第三维（因为每个单元格只能包含一个数字）。因此彩色图像由尺寸为(高x宽x 3）的ndarray表示。

2.15 语言文本数据

如果我们处理文本，情况就会有所不同。用数字表示文本需要两个步骤，构建词汇表（模型知道的所有唯一单词的清单）和嵌入（embedding）。让我们看看用数字表示这个（翻译的）古语引用的步骤：“Have the bards who preceded me left any theme unsung?”

模型需要先训练大量文本才能用数字表示这位战场诗人的诗句。我们可以让模型处理一个小数据集，并使用这个数据集来构建一个词汇表（71,290个单词）：

然后可以将句子划分成一系列“词”token（基于通用规则的单词或单词部分）：

然后我们用词汇表中的id替换每个单词：

这些ID仍然不能为模型提供有价值的信息。因此，在将一系列单词送入模型之前，需要使用嵌入（embedding）来替换token/单词（在本例子中使用50维度的word2vec嵌入)：

你可以看到此NumPy数组的维度为[embedding_dimension x sequence_length]。

在实践中，这些数值不一定是这样的，但我以这种方式呈现它是为了视觉上的一致。出于性能原因，深度学习模型倾向于保留批数据大小的第一维（因为如果并行训练多个示例，则可以更快地训练模型）。很明显，这里非常适合使用reshape()。例如，像BERT这样的模型会期望其输入矩阵的形状为：[batch_size，sequence_length，embedding_size]。