【声明】本博客为学习B站视频小波分解与重构所做笔记,供自己和大家查阅学习,想查看 up 原视频请移步 B 站,侵删。
1.1 小波变换的由来

傅里叶变换基本思想:将信号分解成一系列不同频率的连续正弦波的叠加。
其缺点是,丢失了时间信息,无法判断一个特定频率的信号是在什么时间发生的;只适用于分析平稳信号,不适用于非平稳信号。


短时傅里叶变换的缺点:窗函数的大小和形状与信号的时间和频率没有关系,而且长度固定不变。然而我们一般在分析信号的时候,想要在高频的时候采用小的时间窗(大时间分辨率),在低频的时候采用大的时间窗(大频率分辨率)。该缺点导致
S
T
F
T
STFT
STFT 对时变信号不是很实用。
1.2 小波变换定义及特点

什么叫紧支性? 假设有一个函数 f ( s ) f(s) f(s),其在零值附近函数值都不为零,然而在处零附近之外的地方, f ( s ) f(s) f(s) 的函数值都为零,这个就叫做紧支性。
1.3 连续小波变换

C
W
T
CWT
CWT 的变换结果就是小波系数
C
C
C,这表示在当前时刻
T
T
T,特定频率的成分对信号的贡献程度。


1.4 小波变换的步骤



1.5 离散小波变换

在进行小波变换的时候,对每一个平移参数和缩放因子来进行计算,得到相应的小波系数。这样导致的计算量非常大,这就意味着产生很大的数据量,并且有一些数据是无用的。
如果我们选取缩放因子和平移参数为
2
j
,
j
>
0
且为整数
2^j,j>0且为整数
2j,j>0且为整数,这样对部分的缩放因子和平移参数进行计算,大大减小计算量,从而节省计算时间。
这样的离散小波变换被称为双尺度小波变换,又或者被称为二进小波变换。


1000 个原始数据点,分别对其进行低通和高通滤波,然后对滤波之后的低频信号和高频信号分别进行小波变换,那此时,分别产生了1000个低频小波系数和1000个高频小波系数,这时候为了避免数据量增长,进行降采样处理,从而分别得到 500 个低频小波系数以及 500 个高频小波系数。


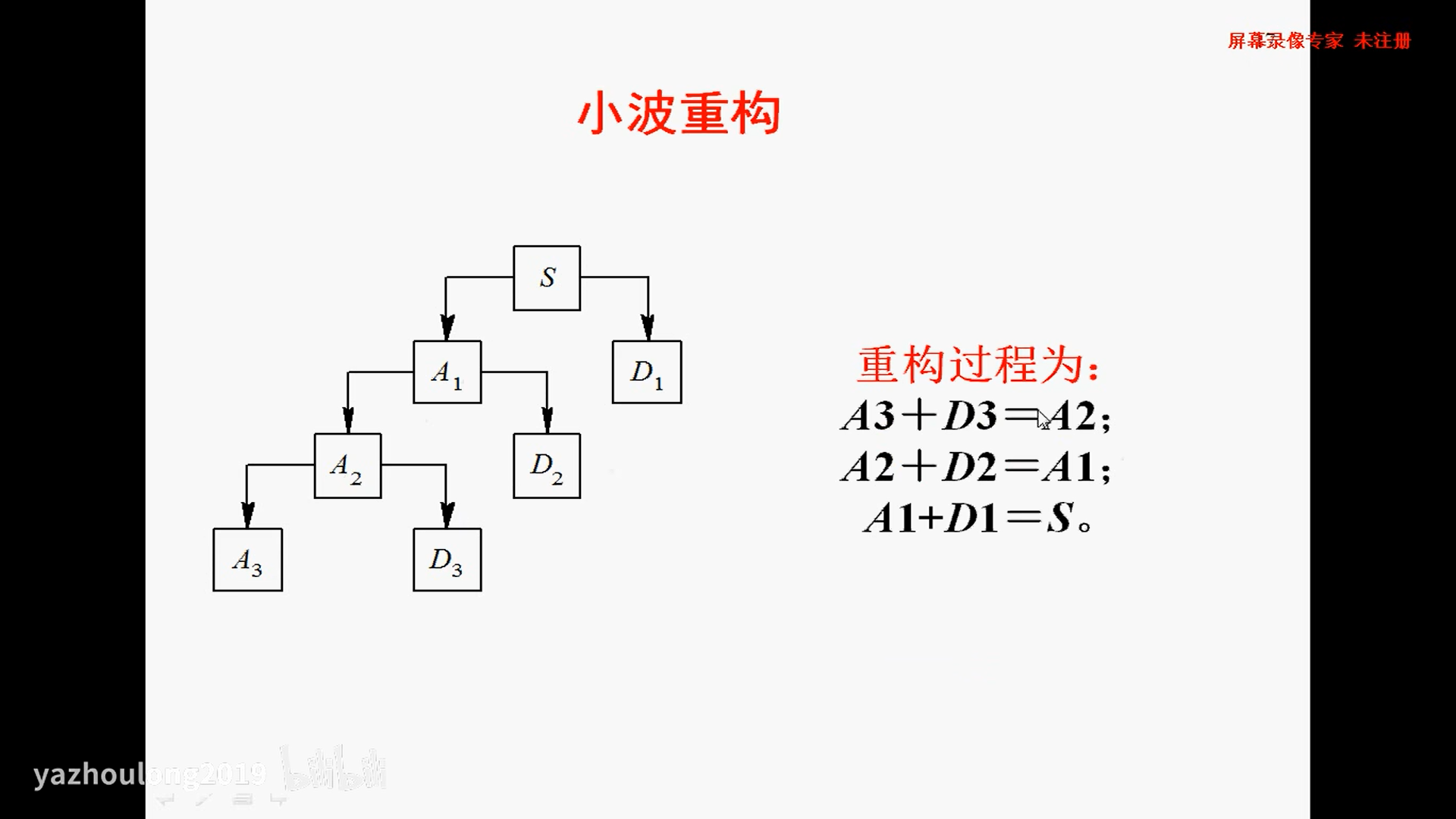
1.6 小波重构