目录
- 一、学习要点
- 二、算法总体思想
- 三、动态规划基本步骤
- 四、矩阵连乘问题
- 4.1 完全加括号的矩阵连乘积
- 4.2 穷举法
- 4.3 动态规划
- 4.3.1 分析最优解的结构
- 4.3.2 建立递归关系
- 4.3.3 计算最优值
- 4.3.4 用动态规划法求最优解
- 五、动态规划算法的基本要素
- 5.1 最优子结构
- 5.2 重叠子问题
- 5.3 备忘录方法
- 六、思考题：捡硬币问题
一、学习要点
理解动态规划算法的概念。
掌握动态规划算法的基本要素：
（1）最优子结构性质
（2）重叠子问题性质
掌握设计动态规划算法的步骤：
(1)找出最优解的性质，并刻划其结构特征。
(2)递归地定义最优值。
(3)以自底向上的方式计算出最优值。
(4)根据计算最优值时得到的信息，构造最优解。
通过应用范例学习动态规划算法设计策略。
（1）矩阵连乘问题；
（2）最长公共子序列；
（3）最大子段和
（4）凸多边形最优三角剖分；
（5）多边形游戏；
（6）图像压缩；
（7）电路布线；
（8）流水作业调度；
（9）背包问题；
（10）最优二叉搜索树。
二、算法总体思想
动态规划算法与分治法类似，其 基本思想也是将待求解问题分解成若干个子问题。
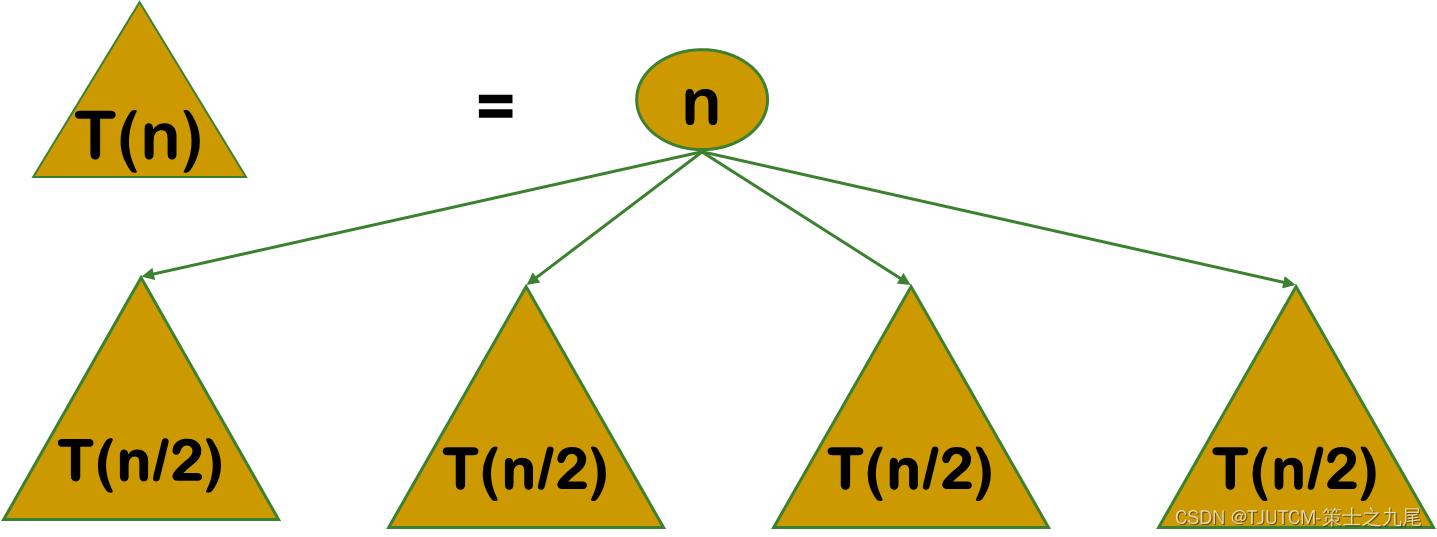
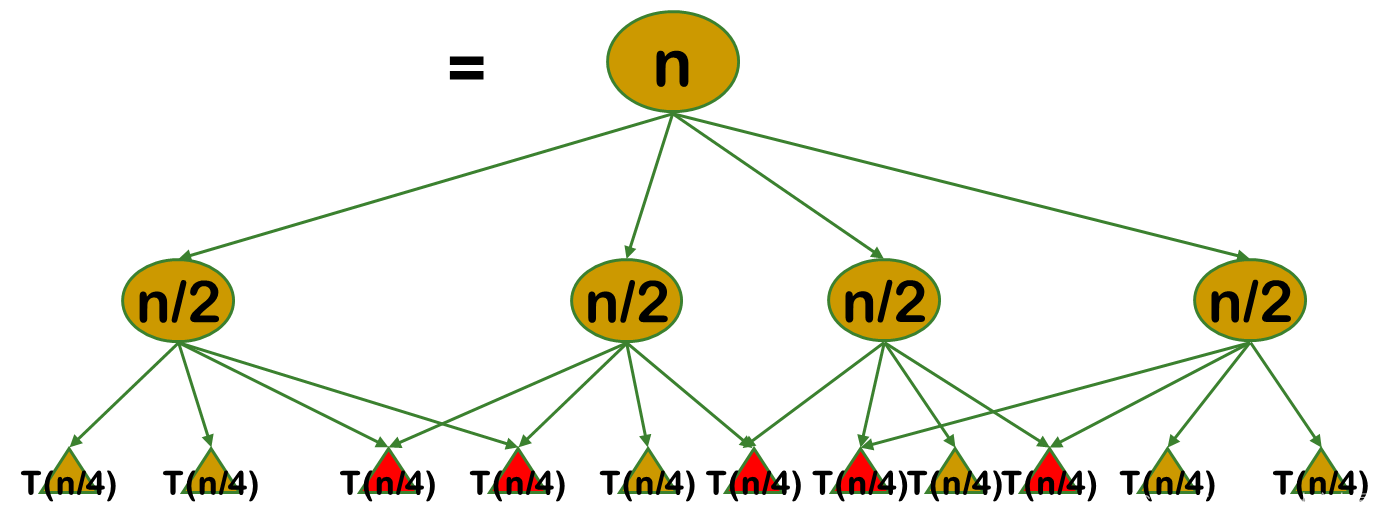
但是经分解得到的子问题往往不是互相独立的。不同子问题的数目常常只有多项式量级。在用分治法求解时，有些子问题被重复计算了许多次。
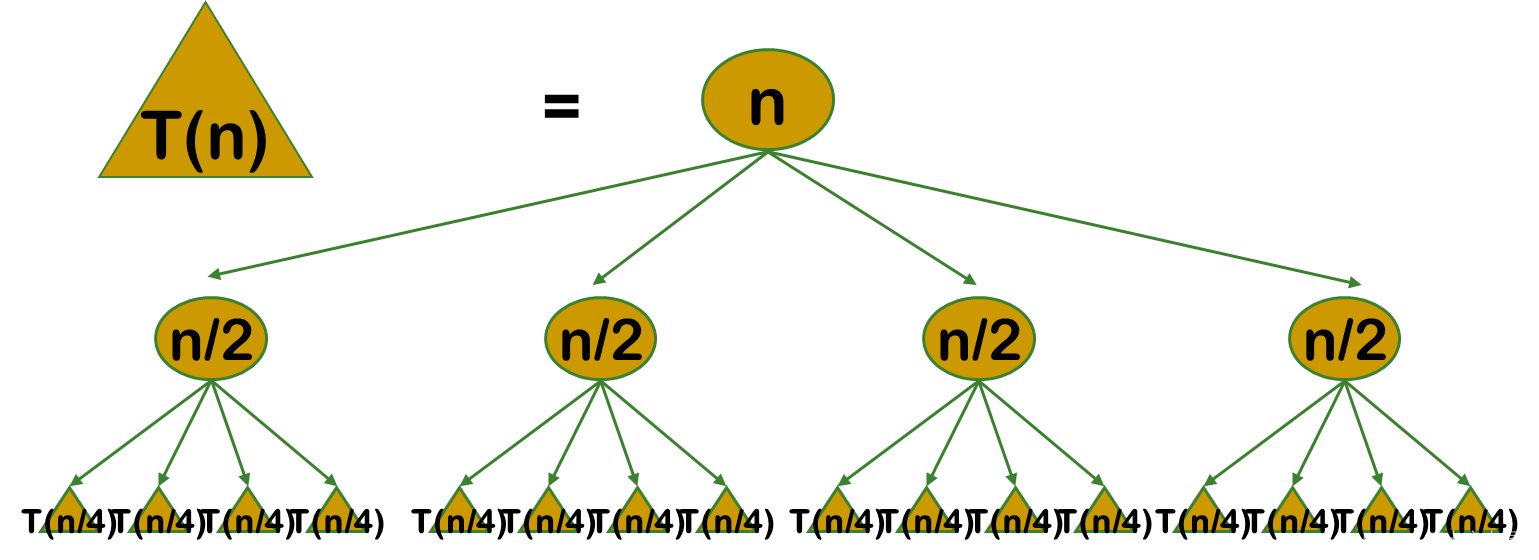
如果 能够保存已解决的子问题的答案，而在需要时再找出已求得的答案，就可以避免大量重复计算，从而得到多项式时间算法。
三、动态规划基本步骤
找出最优解的性质，并刻划其结构特征。
递归地定义最优值。
以自底向上的方式计算出最优值。
根据计算最优值时得到的信息，构造最优解。
四、矩阵连乘问题
问题：给定n个矩阵{A1,A2,…,An}，其中Ai与Ai+1是可乘的，i=1,2,…n-1。我们要计算出这 n个矩阵的连乘积。
因为矩阵乘积满足结合律，所以哪两个矩阵先乘哪两个后乘结果是一样的，但是 计算次数不一样，我们要找计算次数最小的那个次序！
4.1 完全加括号的矩阵连乘积
完全加括号的矩阵连乘积可递归地定义为：
设有四个矩阵A,B,C,D；它们的维数分别是：
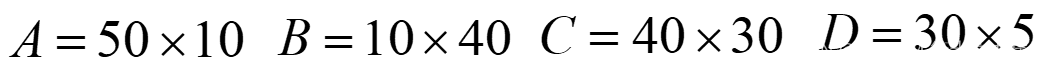
总共有五中完全加括号的方式：
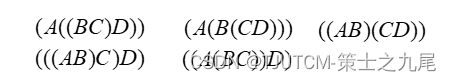
16000, 10500, 36000, 87500, 34500
给定n个矩阵：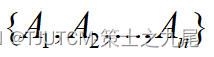
其中Ai与Ai+1是可乘的，i=1,2,…,n-1。考察这n个矩阵的连乘积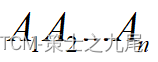
由于 矩阵乘法满足结合律，所以计算矩阵的连乘可以有许多不同的计算次序。这种计算次序可以用加括号的方式来确定。
若一个矩阵连乘积的计算次序完全确定，也就是说该连乘积已完全加括号，则可以依此次序反复调用2个矩阵相乘的标准算法计算出矩阵连乘积。
给定n个矩阵｛A1,A2,…,An｝，其中Ai与Ai+1是可乘的，i=1，2…，n-1。如何确定计算 矩阵连乘积的计算次序，使得依此次序计算矩阵连乘积需要的数乘次数最少。
4.2 穷举法
列举出所有可能的计算次序，并计算出每一种计算次序相应需要的数乘次数，从中找出一种数乘次数最少的计算次序。
算法复杂度分析：
对于n个矩阵的连乘积，设其不同的计算次序为P(n)。
由于每种加括号方式都可以分解为两个子矩阵的加括号问题：(A1…Ak)(Ak+1…An)可以得到关于P(n)的递推式如下：
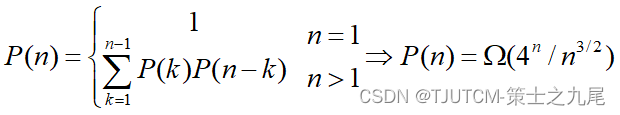
4.3 动态规划
将矩阵连乘积AiAi+1…Aj简记为A[i:j]，这里i≤j
考察计算A[i:j]的最优计算次序。设 这个计算次序在矩阵
Ak和Ak+1之间将矩阵链断开，i≤k<j，则其相应完全加括号方式为：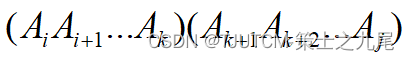
计算量：A[i:k]的计算量加上A[k+1:j]的计算量，再加上A[i:k]和A[k+1:j]相乘的计算量。
4.3.1 分析最优解的结构
特征：计算A[i:j]的最优次序所包含的计算矩阵子链 A[i:k]和A[k+1:j]的次序也是最优的。
矩阵连乘计算次序问题的最优解包含着其子问题的最优解。这种性质称为最优子结构性质。问题的最优子结构性质是该问题可用动态规划算法求解的显著特征。
4.3.2 建立递归关系
设计算A[i:j]，1≤i≤j≤n，所需要的最少数乘次数m[i,j]，则原问题的最优值为m[1,n]
当i=j时，A[i:j]=Ai，因此，m[i,i]=0，i=1,2,…,n
当i<j时，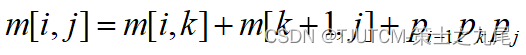
可以递归地定义m[i,j]为：
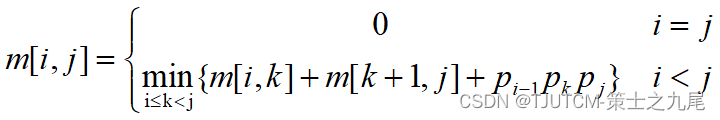
（k的位置只有j-i种可能）
4.3.3 计算最优值
对于1≤i≤j≤n不同的有序对(i,j)对应于不同的子问题。因此，不同子问题的个数最多只有
由此可见，在递归计算时，许多子问题被重复计算多次。这也是该问题可用动态规划算法求解的又一显著特征。
用动态规划算法解此问题，可依据其递归式以自底向上的方式进行计算。在计算过程中，保存已解决的子问题答案。每个子问题只计算一次，而在后面需要时只要简单查一下，从而避免大量的重复计算，最终得到多项式时间的算法。
1.计算A1，A2，A3，A4，A5，A6
2.计算（A1A2），（A2A3），（A3A4），（A4A5），（A5A6）
3.计算（A1A2A3），…，（A4A5A6）
4.计算A[1,4],A[2,5],A[3,6]
5.计算A[1,5],A[2,6]
6.计算A[1,6]
4.3.4 用动态规划法求最优解
void MatrixChain(int *p，int n，int **m，int **s)
{
for (int i = 1; i <= n; i++) m[i][i] = 0;
for (int r = 2; r <= n; r++)
for (int i = 1; i <= n - r+1; i++) {
int j=i+r-1;
m[i][j] = m[i+1][j]+ p[i-1]*p[i]*p[j];
s[i][j] = i;
for (int k = i+1; k < j; k++) {
int t = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j];
if (t < m[i][j]) { m[i][j] = t; s[i][j] = k;}
}
}
}
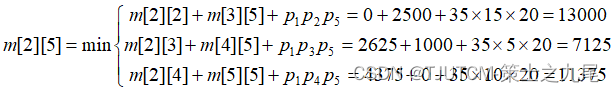
算法复杂度分析：
算法matrixChain的主要计算量取决于算法中对r，i和k的3重循环。循环体内的计算量为O(1)，而3重循环的总次数为O(n3)。因此算法的计算时间上界为O(n3)。算法所占用的空间显然为O(n2)。
五、动态规划算法的基本要素
5.1 最优子结构
矩阵连乘计算次序问题的最优解包含着其子问题的最优解。这种性质称为最优子结构性质。
在分析问题的最优子结构性质时，所用的方法具有普遍性：首先假设由问题的最优解导出的子问题的解不是最优的，然后再设法说明在这个假设下可构造出比原问题最优解更好的解，从而导致矛盾。
利用问题的最优子结构性质，以自底向上的方式 递归地从子问题的最优解逐步构造出整个问题的最优解。最优子结构是问题能用动态规划算法求解的前提。
同一个问题可以有多种方式刻划它的最优子结构，有些表示方法的求解速度更快（空间占用小，问题的维度低）
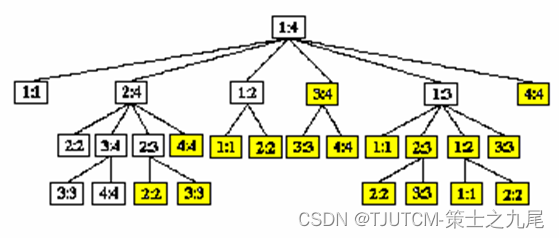
5.2 重叠子问题
递归算法求解问题时，每次产生的子问题并不总是新问题，有些子问题被反复计算多次。这种性质称为子问题的重叠性质。
动态规划算法，对每一个子问题只解一次，而后将其解保存在一个表格中，当再次需要解此子问题时，只是简单地用常数时间查看一下结果。
通常不同的子问题个数随问题的大小呈多项式增长。因此用动态规划算法只需要多项式时间，从而获得较高的解题效率。
5.3 备忘录方法
备忘录方法的控制结构与直接递归方法的控制结构相同，区别在于备忘录方法为每个解过的子问题建立了备忘录以备需要时查看，避免了相同子问题的重复求解。
int LookupChain(int i，int j)
{
if (m[i][j] > 0) return m[i][j];
if (i == j) return 0;
int u = LookupChain(i，i) + LookupChain(i+1，j) + p[i-1]*p[i]*p[j];
s[i][j] = i;
for (int k = i+1; k < j; k++) {
int t = LookupChain(i，k) + LookupChain(k+1，j) + p[i-1]*p[k]*p[j];
if (t < u) { u = t; s[i][j] = k;}
}
m[i][j] = u;
return u;
}
六、思考题：捡硬币问题
现有n个硬币按顺序依次排列在你面前，可以看为一个数组coins[]={5,1,2,10,6,2}，请在此中捡取若干个硬币，使得所取硬币累加值最大，捡取个数不限，但相邻两个硬币不得捡取，请设计相应算法，并输出累加值
提示：硬币面值必须是正数，不能有负值。建立数组dp[i]存储选取前i个硬币的累加值
