stl格式-3D三角形

文章目录

什么是stl文件?
格式首选
stl的语法
- 1.这是一个stl格式的文件:(ASCII码)
- 2.下面先举个例子(难度略微提示)
- - 补充:关于\<\<我试了一下:这个法线你随便写好像也没问题\>>
- 3.来个立方体
- 4.最后再写一个由三个直角形组成的立方体(直棱锥)
- 5.amend 修正(右手定则,法线向外)

什么是stl文件?

首先说一下,这个stl不是cpp中的stl库.

指的是以.stl结尾的文件(S T ereo L ithography)

STL（Standard Tessellation Language）：STL是一种用于表示三角网格的一种文件格式，它将模型表示为一系列连接的三角形。STL文件通常分为两种类型：ASCII和二进制。ASCII STL文件使用文本表示，包含逐个定义三角面片的数据，而二进制STL文件则使用二进制编码，更紧凑且通常更常用。STL文件广泛用于3D打印和计算机辅助设计（CAD）等领域。

格式首选

STL 文件格式的 ASCII 版本是用纯 ASCII 编写的。但是，由于文件格式较大，因此没有选择该文件格式作为使用的首选格式。(但是二进制无法编写,我们使用ASCII码来编写)

以下从文件大小,读写速度,数据精度,文件解析效率四个方面来解释二进制格式的优势:

文件大小：二进制格式的STL文件通常比ASCII格式更小，因为二进制格式使用固定长度的数据表示，而ASCII格式使用可变长度的文本表示。这意味着二进制格式可以更有效地存储模型的几何数据，减少存储和传输的开销。
读写速度：由于二进制格式的数据是以二进制编码存储的，相比于ASCII格式，读取和写入二进制STL文件的速度更快。二进制数据可以直接按字节进行读写，无需进行解析和转换操作，因此在处理大型模型或需要频繁读写的场景下，二进制格式能提供更高的效率。
数据精度：二进制格式的STL文件可以提供更高的数据精度。由于ASCII格式使用文本表示数字，存在精度损失和舍入误差的问题。而二进制格式使用固定大小的浮点数表示，可以保持更高的精度，并减少舍入误差。
文件解析效率：由于二进制格式的STL文件直接存储了几何数据的二进制表示，解析器可以更快速地读取和处理文件。相比之下，解析ASCII格式的STL文件需要进行文本解析和字符串处理，可能会更耗时。

stl的语法

1.这是一个stl格式的文件:(ASCII码)

solid name
    facet normal ni nj nk
        outer loop
            vertex v1x v1y v1z
            vertex v2x v2y v2z
            vertex v3x v3y v3z
        endloop
    endfacet
endsolid name

聪明的小伙伴应该意识到了:
ni nj nk
与
v1x v1y v1z
v2x v2y v2z
v3x v3y v3z
就是我们要填入的参数
{
ni nj nk代表法线的方向
v1x v1y v1z是顶点1的坐标,
然后是顶点2,顶点3的坐标

然后法线(高一知识终于用到了,然后考研也考)的方向可以通过计算三个顶点的叉乘得到.[这是一种方法(还有就是,如果你不会求法线也不要怕,后面写的很详细)]

或者是你已经有了一个具体的模型,然后你可以使用Blender软件来获取相关数据[这是第二种方法,在这篇文章,咱们仅仅只谈方法一,因为方法二是使用轮子,现在咱们来沉下心来造轮子!]
}

然后name想填啥就填啥,只要保证solid name与endsolid name保持一致就OK了!!!

2.下面先举个例子(难度略微提示)

(其实难度也不是很高,难度在于:网上还没有中文资料,大多数都是英文的,然后即使翻译过来,如果不是专业的翻译人员,翻译过来的意思也不是那么通俗易懂)

现在假设有一个平面三角形,顶点坐标为:
顶点一:(0,0,0)
顶点二:(1,0,0)
顶点三:(0,1,0)
(这个也很简单,大家可以在纸上画一下)

然后我们就要填入数据了!

首先,计算就是计算法线的方向.法线的方向可以通过计算任意两条边的叉积得到.
我们计算顶点2和顶点1以及顶点3与顶点1的向量:
向量a = (1,0,0)-(0,0,0) = (1,0,0) = (a₁,a₂,a₃)
向量b = (0,1,0)-(0,0,0) = (0,1,0) = (b₁,b₂,b₃)

法线的方向就直接axb得到:

ni nj nk = axb = (0,0,1)

然后,至于为啥 (1,0,0) $X$ (0,1,0) = (0,0,1)?

根据叉积的计算公式为：23 32, 31 13,12 21
$a \times b$ = ( $a_{2} b_{3}$ - $a_{3} b_{2}$ , $a_{3} b_{1}$ - $a_{1} b_{3}$ , $a_{1} b_{2}$ - $a_{2} b_{1}$ )

=(0x0-0x1, 0x0-1x0, 1x1-0x0)

=(0, 0 ,1)

(然后,再强调一下,叉积和矩阵相乘是两回事!!!)

至于三维的叉积公式怎么记?可以看下图:记住23 31 自然就记住了全部了

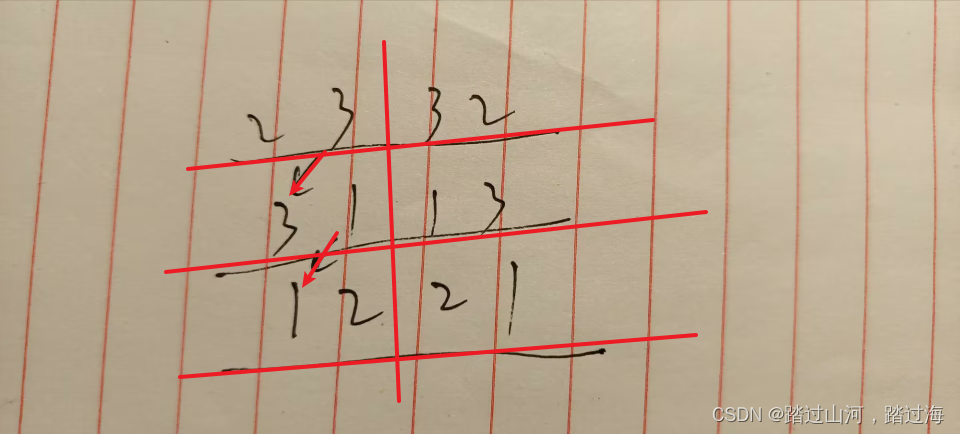
在这里插入图片描述

因此,法线就是(0,0,1)
所以,我们完成的stl文件格式如下:

solid test
	facet normal 0 0 1         //我试了一下:这个法线你随便写好像也没问题
	outer loop
	vertx 0 0 0
	vertx 1 0 0
	vertx 0 1 0
	endloop
	endfacet
endsolid test

补充:关于<<我试了一下:这个法线你随便写好像也没问题>>

法线你随便写,确实还是可以正常显示stl的3d图像的,但是颜色好像变深或者变浅了

这就是涉及到法线的作用了:

STL文件中的法线向量是用于确定三角面片的朝向和光照效果的。法线向量指示了面片的表面方向，使软件能够确定如何着色和渲染模型。

当你随意更改法线向量时，STL文件仍然可以显示出来，但视觉效果可能会发生变化。由于法线向量的改变，渲染引擎可能会根据新的法线方向重新计算面片的光照效果，导致颜色变深或变浅。

然而，这种方式并不代表结果是正确的或符合实际形状的。正确的法线方向对于准确显示和渲染三维模型非常重要。如果法线方向错误或不一致，可能会导致不自然的阴影、光照效果不良或渲染问题。

因此，为了正确呈现和渲染模型，请确保为每个面片定义正确的法线方向，并确保它们与实际表面法线方向相匹配。这样可以确保模型在渲染时获得更准确的外观和光照效果。

3.来个立方体

其实一组这个,就代表一个立方体

facet normal ni nj nk
    outer loop
        vertex v1x v1y v1z
        vertex v2x v2y v2z
        vertex v3x v3y v3z
    endloop
endfacet


然后一个正方形需要两组,所以就是十二组

solid test
  facet normal 0 0 1
    outer loop
      vertex 0 0 0
      vertex 1 0 0
      vertex 0 1 0
    endloop
  endfacet
  facet normal 0 0 1
    outer loop
      vertex 1 1 0
      vertex 0 1 0
      vertex 1 0 0
    endloop
  endfacet
  facet normal 0 0 -1
    outer loop
      vertex 0 0 1
      vertex 0 1 1
      vertex 1 0 1
    endloop
  endfacet
  facet normal 0 0 -1
    outer loop
      vertex 1 1 1
      vertex 1 0 1
      vertex 0 1 1
    endloop
  endfacet
  facet normal 0 1 0
    outer loop
      vertex 0 1 0
      vertex 1 1 1
      vertex 0 1 1
    endloop
  endfacet
  facet normal 0 1 0
    outer loop
      vertex 1 1 0
      vertex 0 1 0
      vertex 1 1 1
    endloop
  endfacet
  facet normal 0 -1 0
    outer loop
      vertex 0 0 0
      vertex 0 0 1
      vertex 1 0 0
    endloop
  endfacet
  facet normal 0 -1 0
    outer loop
      vertex 1 0 1
      vertex 1 0 0
      vertex 0 0 1
    endloop
  endfacet
  facet normal 1 0 0
    outer loop
      vertex 1 0 0
      vertex 1 1 1
      vertex 1 0 1
    endloop
  endfacet
  facet normal 1 0 0
    outer loop
      vertex 1 1 0
      vertex 1 0 0
      vertex 1 1 1
    endloop
  endfacet
  facet normal -1 0 0
    outer loop
      vertex 0 0 0
      vertex 0 1 0
      vertex 0 0 1
    endloop
  endfacet
  facet normal -1 0 0
    outer loop
      vertex 0 1 1
      vertex 0 0 1
      vertex 0 1 0
    endloop
  endfacet
endsolid test

在这里插入图片描述

4.最后再写一个由三个直角形组成的立方体(直棱锥)

solid Cylinder
  facet normal 0.0 1.0 0.0
    outer loop
      vertex 0.0 0.0 0.0
      vertex 0.0 0.0 1.0
      vertex 1.0 0.0 0.0
    endloop
  endfacet  

  facet normal 0.0 0.0 1.0
    outer loop
      vertex 0.0 0.0 0.0
      vertex 1.0 0.0 0.0
      vertex 0.0 1.0 0.0
    endloop
  endfacet

  facet normal 0.0 0.0 1.0
    outer loop
      vertex 0.0 0.0 0.0
      vertex 0.0 1.0 0.0
      vertex 0.0 0.0 1.0
    endloop
  endfacet

  facet normal 1.0 0.0 0.0
    outer loop
      vertex 0.0 0.0 1.0
      vertex 1.0 0.0 0.0
      vertex 0.0 1.0 0.0
    endloop
  endfacet
  
endsolid Cylinder

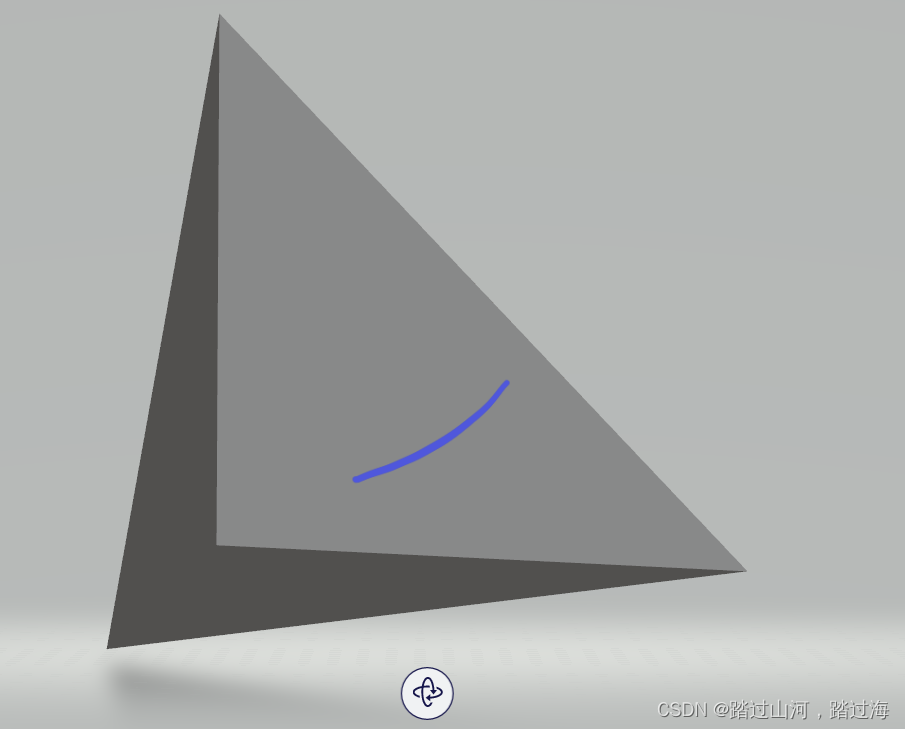
在这里插入图片描述

5.amend 修正(右手定则,法线向外)

每组中的三个vertex,要按逆时针排放,按照逆时针排放三个顶点组成的三角形的法向量是朝外的,所以这个三个vertex的顺序有说法.

(相反,你不按逆时针排放,则法向量方向朝向里面)

vertex 0.0 1.0 0.0
vertex 0.0 0.0 0.0
vertex 0.0 0.0 1.0

然后就是: $f a ce t$ $n or ma l$ $0.0$ $- 1.0$ $0.0$ 表示法向量,但是 $s tl 格式$ 似乎并没有采用这个法向量的方向,正如这个例子,不管你写成(0.0 -1.0 0.0)还是(0.0 1.0 0.0),效果都是不变的,法向量方向的确定权:取决于vertex三兄弟的顺序!

solid Cylinder
  facet normal 0.0 -1.0 0.0
    outer loop
      vertex 0.0 0.0 1.0
      vertex 0.0 0.0 0.0
      
      vertex 1.0 0.0 0.0
    endloop
  endfacet  

  facet normal 0.0 0.0 -1.0
    outer loop
      vertex 1.0 0.0 0.0
      vertex 0.0 0.0 0.0  
      vertex 0.0 1.0 0.0
    endloop
  endfacet

  facet normal 	-1.0 0.0 0.0
    outer loop
      vertex 0.0 1.0 0.0
      vertex 0.0 0.0 0.0
      vertex 0.0 0.0 1.0
    endloop
  endfacet

    facet normal -1.0 -1.0 -1.0
    outer loop
      vertex 0.0 0.0 1.0
      vertex 1.0 0.0 0.0
      vertex 0.0 1.0 0.0
    endloop
  endfacet
  
endsolid Cylinder

solid Cylinder
  facet normal 0.0 -1.0 0.0
    outer loop
      vertex 0.0 0.0 1.0
      vertex 0.0 0.0 0.0
      
      vertex 1.0 0.0 0.0
    endloop
  endfacet  

  facet normal 0.0 0.0 -1.0
    outer loop
      vertex 1.0 0.0 0.0
      vertex 0.0 0.0 0.0  
      vertex 0.0 1.0 0.0
    endloop
  endfacet

  facet normal 	-1.0 0.0 0.0
    outer loop
      vertex 0.0 1.0 0.0
      vertex 0.0 0.0 0.0
      vertex 0.0 0.0 1.0
    endloop
  endfacet

    facet normal -1.0 -1.0 -1.0
    outer loop
      vertex 0.0 0.0 1.0
      vertex 1.0 0.0 0.0
      vertex 0.0 1.0 0.0
    endloop
  endfacet
  
endsolid Cylinder