寻找右区间(排序 + 二分查找)
题目链接

理解题目
-
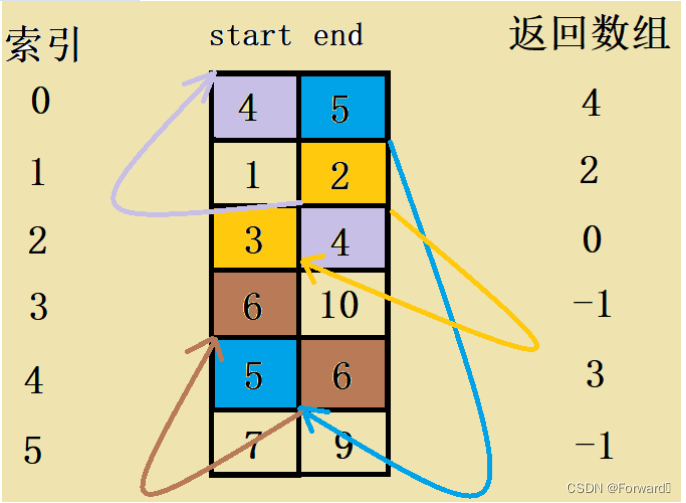
题目给定一个具有n行2列的二维数组
intervals,对于intervals的每一行元素i,就表示一个区间数组,intervals[i][0]即这个区间数组的起始位置start,intervals[i][1]就是区间数组的结束位置end。同时,题目告诉我们对于每一个区间数组i,他们的start都不同 -
题目要我们找的,就是对于每一个区间数组
i,寻找一个start满足start >= end,如果存在该start,就要使start最小化,即使start - end的值最小 -
找到
start后,就将这个start的索引记录到返回数组(如果这个start位于第n个区间数组,那么索引就是n - 1),否则记录-1
思路
最简单的思想,就是利用两层循环来求得答案。第一层循环用来遍历每个区间数组intervers[i],第二层循环用来找到每一个intervals[i][start]的end,但显然,这个方法的时间复杂度为O(N2),效率低,故不做讨论
应该想到,我们应该对每个区间数组进行排序,以此来优化我们的查找。
需要解决以下几个问题:
- 我们应该以每个区间的
start为标准还是以end为标准进行排序?
- 要清楚的一点是,本题我们查找的是符合条件的
start,以此来满足start >= intervals[i][start],因此,如果要优化查找start的效率,就应该以start为标准对每个区间数组进行排序。
- 找到符合条件的
start后,要将其所在区间数组的索引记录在返回数组,但是将区间数组排序后,索引值不久变了吗?怎么解决?
- 我们可以新建一个结构体数组
StartNode用来存储每个区间数组的start以及索引index,这样就不会丢失正确定索引了。
typedef struct Node
{
int start; //区间数组的start
int index; //区间数组的索引
}Node;
int cmp(const void* num1, const void* num2)
{
return ((Node*)num1)->start - ((Node*)num2)->start;
}
int* findRightInterval(int** intervals, int intervalsSize, int* intervalsColSize, int* returnSize){
//创建一个结构体数组
//用来存储每个区间数组的start,及其索引
Node* StartNode = (Node*)malloc(sizeof(Node) * intervalsSize);
for (int i = 0; i < intervalsSize; i++)
{
StartNode[i].start = intervals[i][0];
StartNode[i].index = i;
}
//对区间数组的start进行升序排序
qsort(StartNode, intervalsSize, sizeof(Node), cmp);
………………
}
解决了这两个问题,就可以开始正式查找了:
利用一层循环遍历每个区间数组的end,接着利用二分查找在StartNode中查找符合条件的start,同时将索引录入返回数组,如果没有找到,就录入-1。
实现代码
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
typedef struct Node
{
int start;
int index;
}Node;
int cmp(const void* num1, const void* num2)
{
return ((Node*)num1)->start - ((Node*)num2)->start;
}
int* findRightInterval(int** intervals, int intervalsSize, int* intervalsColSize, int* returnSize){
int row = intervalsSize;
int col = *intervalsColSize;
//创建一个结构体数组
//用来存储每个区间数组的start,及其索引
Node* StartNode = (Node*)malloc(sizeof(Node) * intervalsSize);
for (int i = 0; i < intervalsSize; i++)
{
StartNode[i].start = intervals[i][0];
StartNode[i].index = i;
}
//对区间数组的start进行升序排序
qsort(StartNode, intervalsSize, sizeof(Node), cmp);
int* ret = (int*)malloc(sizeof(int) * intervalsSize);
*returnSize = intervalsSize;
//遍历原数组的每一个end
//同时在已经有序的升序数组中找到第一个大于end的start
//并将其索引记录到返回数组,如果找不到,就记录为-1
for (int i = 0; i < intervalsSize; i++)
{
int end_i = intervals[i][1];
int target = -1; //target即正确的索引位置,初始化为-1代表假定找不到符合条件的start
//利用二分法找到 start >= end,同时又是最小的start及其索引
int left = 0;
int right = intervalsSize - 1;
while (left <= right)
{
int mid = (right - left) / 2 + left;
if (StartNode[mid].start >= end_i)
{
target = StartNode[mid].index;
right = mid - 1;
}
else
left = mid + 1;
}
//将索引录入返回数组
ret[i] = target;
}
//销毁申请的动态内存
free(StartNode);
return ret;
}