目录

题目：

示例：

分析：

代码：

---

题目：

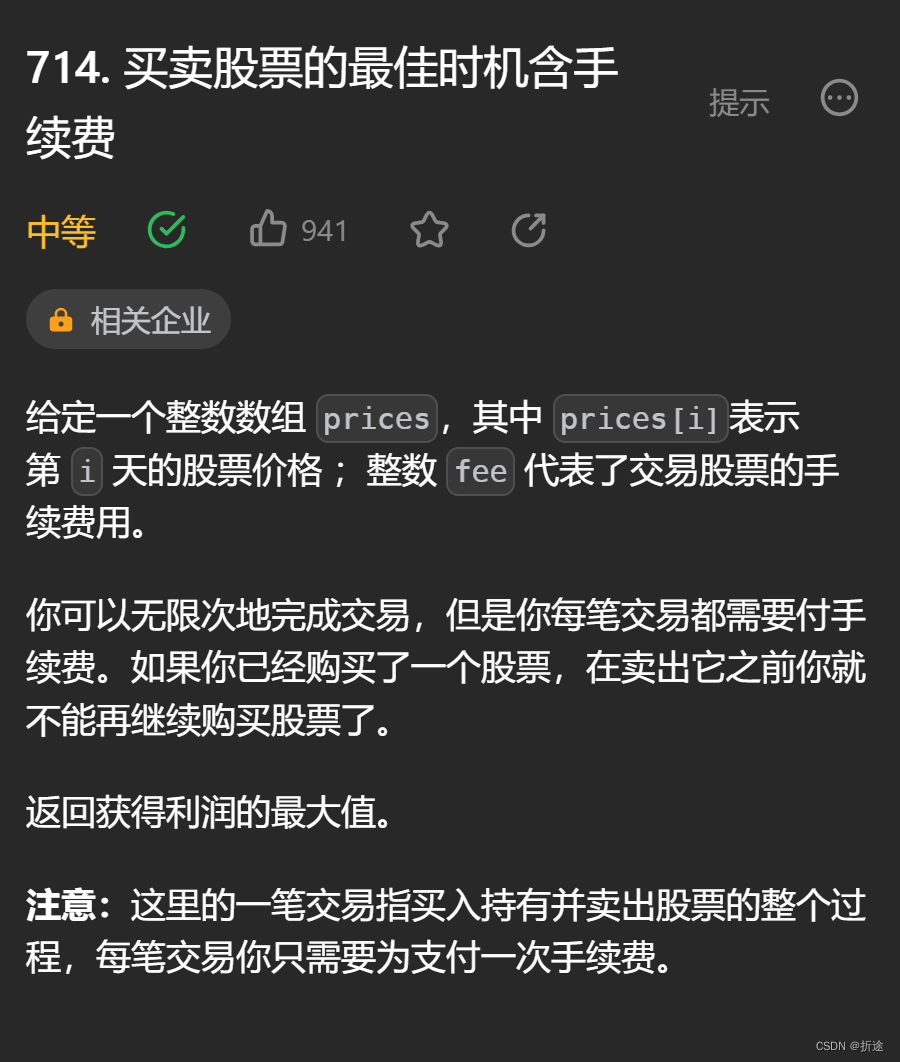
示例：

分析：

这是力扣里动态规划类题目里的一道系列题目，买卖股票，直接在题库里搜就能搜到这一系列。

 我建议各位可以先去做一下这系列的其他题目，至少是吧买卖股票的最佳时机1和2做一下。

那么接下来我们来分析分析这道题怎么做。

首先是给一个数组，第 i 个数表示第 i 天的股票价格，我们如果没有股票就可以按照这个价格买入。如果我们手上有股票，就可以按照这个价格卖出，不过卖出的时候需要扣除一笔手续费。

问我们最多能获利多少。

那么我们直接用动态规划来做。

首先我们需要先定义好dp数组的含义。这个先放一边。

我们来分析一下，在本题中，我们的状态是持有股票和没有持有股票两种状态。

而我第 i 天持有股票时能拥有的最多收益是我第 i - 1天持有股票时能拥有的最多收益或者是我第 i - 1天没有持有股票时的最多收益再扣除第 i 天的股票价格，因为我第 i - 1 天没有股票的话，我在第 i 天有股票那就只能是在第 i 天买入股票。

在这两种情况下我们选一个最大值作为我们第 i 天持有股票时能拥有的最多收益。

而我第 i 天没有股票时能拥有的最多收益则是我第 i - 1 天没有股票的最多收益或者是我第 i - 1 天持有股票时拥有的最多收益再加上第 i 天的股票价格再扣除手续费。

在这两种情况下我们选一个最大值作为我们第 i 天没有股票时拥有的最多收益。

这就是我们的递推公式。

由于我们只有两种状态需要保存，因此dp数组的大小为2*n，n是股票价格数组的长度。

我们规定dp[ 0 ][ i ]存放的是第 i 天持有股票时拥有的最多收益。

规定dp[ 1 ][ i ]存放的是第 i 天没有股票时拥有的最多收益。

递推公式就是这样：

 接下来的问题就是初始化。由于我们的递推公式里有 i - 1 的操作，因此 i 至少等于1，等于0就会下标越界。所以我们需要初始化的是dp[ 0 ][ 0 ]和dp[ 1 ][ 0 ]

dp[ 0 ][ 0 ]的含义就是在第0天我持有股票时拥有的最多利润，那么第0天我要持有股票，那么只能是在第0天就买了股票，所以dp[ 0 ][ 0 ]初始化成负的第0天的股票价格。

而dp[ 1 ][ 0 ]的含义就是在第0天我不持有股票时拥有的最多利润，直接为0即可。

接下来我们用递推公式填满dp数组，最后返回dp[ 1 ][ n - 1 ]，n为股票价格数组的长度。

为什么是dp[ 1 ][ n - 1 ]而不是dp[ 0 ][ n - 1 ]，因为我都到最后一天了，手里有没有股票我后面都卖不掉了，所以自然是手上的股票都抛完了的情况下我的利润最大。

代码：

class Solution {
public:
    int maxProfit(vector<int>& prices, int fee) {
        vector<vector<int>>dp(2,vector<int>(prices.size()));
        //dp[0]持有股票,dp[1]不持有股票
        dp[0][0]=-prices[0];
        for(int i=1;i<prices.size();i++){
            dp[0][i]=max(dp[0][i-1],dp[1][i-1]-prices[i]);
            dp[1][i]=max(dp[1][i-1],dp[0][i-1]+prices[i]-fee);
        }
        return dp[1][prices.size()-1];
    }
};