归并（merge）排序

news2024/11/25 21:20:57

归并（merge）排序也是采用分而治之的思想，其采用二分法将待排列数组分成若干个子数组。然后将相邻的子数组进行归并成新的有序子数组，然后在新的子数组的基础上在进行归并成新的有序数组，直至归并成一个整体有序的数组。

算法思想
归并排序的最基本思想就是将一个数组拆分成两个数组，然后对每个子数组进行排序，然后将两个有序子数组归并成一个有序的数组。

归并排序算法大致可以分为两步，如下图所示：
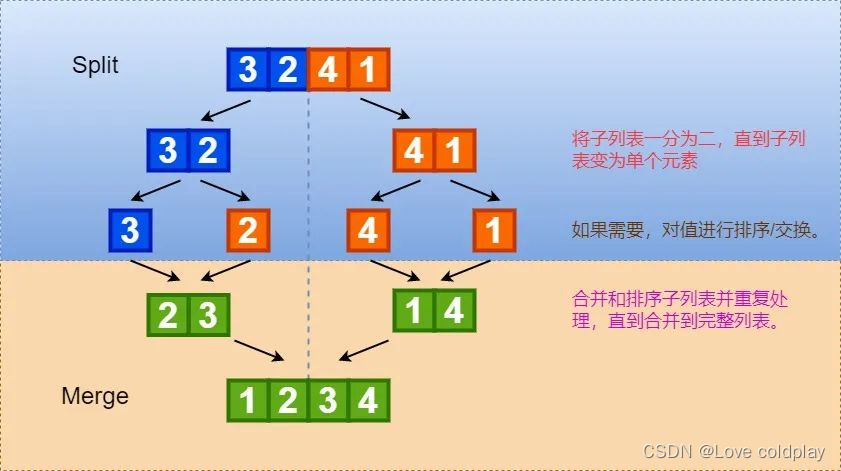
在这里插入图片描述

分解（Split）
如果数组的长度为1，则认为这个数组已经有序，直接返回即可。
如果数组长度大于1，则将该数组从中间分解成两个子数组，对每个子数组再进行分解，直至每个子数组的长度为1。
归并（Merge）
将每个相邻子数组进行排序归并，直至所有子数组排序归并完成。
最终归并出来的数组就是排序后的有序数组。
下面我们重点讲一下排序归并的过程和代码实现思路:

以数组A{2, 3, 1, 4}为例，首先拷贝一份A存于B，由于B的左右索引分别为l=0和r=3，所以其mid = (l+r)/2 ，由于l和r均为int类型，因此mid=1；根据归并排序算法中的分解方法，我们将{2, 3}（对应B中[l, mid]这段区间）和{1, 4}（对应B中[mid+1, r]这段区间）作为A的拆分出来的两个子数组（且他们已经有序了，可以直接进行排序归并了）。使用索引i和j分别指向这两个子数组的第一个元素，索引k指向原数组A的第一个元素。

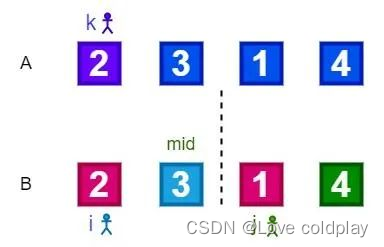
在这里插入图片描述

比较B[i]和B[j]的大小，此时2>1，因此将B[j]的值1赋值给A[k]，然后j和k都往后移动一位。结果如下图所示：

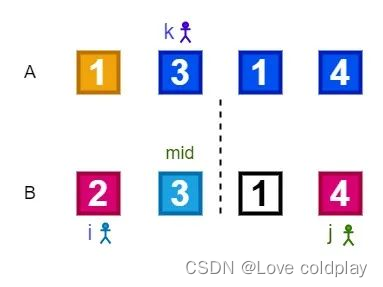
在这里插入图片描述

然后再次比较B[i]和B[j]的大小，此时2<4，因此将B[i]的值2赋值给A[k]，然后i和k都往后移动一位。结果如下图所示：

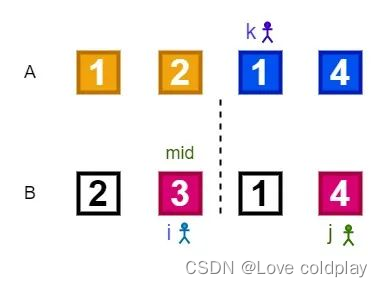
在这里插入图片描述

接下来继续比较B[i]和B[j]的大小，此时3<4，因此将B[i]的值3赋值给A[k]，然后i和k都往后移动一位。结果如下图所示：

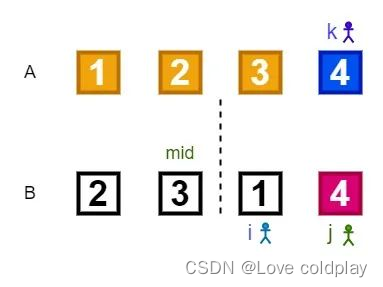
在这里插入图片描述

此时i>mid，即子数组{2, 3}已经全部归并至A，子数组{1, 4}仅剩一个元素4，将B[j]的值4赋值给A[k]，然后i和k都往后移动一位，此时归并完成。如下图所示：

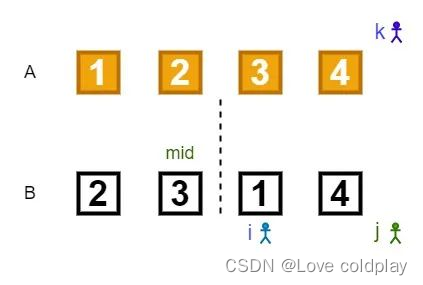
在这里插入图片描述

代码实现

#include <algorithm>
#include <iostream>

// 将arr[l,mid]和arr[mid+1,r]的数组进行归并
template <typename T>
void merge_(T arr[], int l, int mid, int r) {
    T *tmp = new T[r - l + 1];
    for (int i = l; i <= r; ++i)
        tmp[i - l] = arr[i];  // tmp从0开始，对应的arr有l个偏移

    int i = l, j = mid + 1;
    for (int k = l; k <= r; ++k) {
        if (i > mid)  // 如果左半部分元素已经全部处理完毕
        {
            arr[k] = tmp[j - l];
            j++;
        } else if (j > r)  // 如果右半部分元素已经全部处理完毕
        {
            arr[k] = tmp[i - l];
            i++;
        } else if (tmp[i - l] < tmp[j - l])  // i所指元素(对应的是tmp[i-l]) <
            // j所指元素(对应的是tmp[j-l])
        {
            arr[k] = tmp[i - l];
            i++;
        } else  // i所指元素(对应的是tmp[i-l]) >= j所指元素(对应的是tmp[j-l])
        {
            arr[k] = tmp[j - l];
            j++;
        }
    }
    delete[] tmp;
}

// 递归使用归并排序,对arr[l...r]的范围进行排序
template <typename T>
void mergeSort_(T arr[], int l, int r) {
    if (l >= r) return;

    int mid = (l + r) / 2;
    mergeSort_(arr, l, mid);
    mergeSort_(arr, mid + 1, r);
    merge_(arr, l, mid, r);
}

template <typename T>
void mergeSort(T arr[], int n) {
    mergeSort_(arr, 0, n - 1);
}

int main() {
    int arr[] = {3, 5, 2, 1, 4};
    mergeSort(arr, 5);
    for (int i = 0; i < 5; ++i) {
        std::cout << arr[i] << " ";
    }
    std::cout << std::endl;
    return 0;
}