1. 数据结构的定义

在计算机科学领域，数据结构是一种数据组织、管理和存储格式，通常被选择用来高效访问数据。

2. 二分查找

2.1 二分查找的定义

二分查找算法也称折半查找，是在一个升序数组中，查找要需要找的值，如果找到就返回该数的索引，否则返回-1

2.2 二分查找分析

(1) 定义两个变量分别是i和j，i默认的索引为0，j默认的索引为指定数组的最后一个元素的索引
(2) 如果i>j，说明没找到该元素
(3) 定义一个变量m，m为中间索引
(4) 如果target < a[m]，j = m-1
(5)如果a[m] < target，i = m+1
(6)如果 a[m] = target，说明找到，返回该值的索引

2.3 二分查找实现

 // 二分查找 - 基础版
    public static int binarySearch(int a[], int target) {
        int i = 0;
        int j = a.length - 1;
        while (i <= j) {
            int m = (i + j) / 2;
            if (a[m] < target) {
                i = m + 1;
            } else if (target < a[m]) {
                j = m - 1;
            } else {
                return m;
            }
        }
        return -1;
    }

2.4 二分查找算法图解

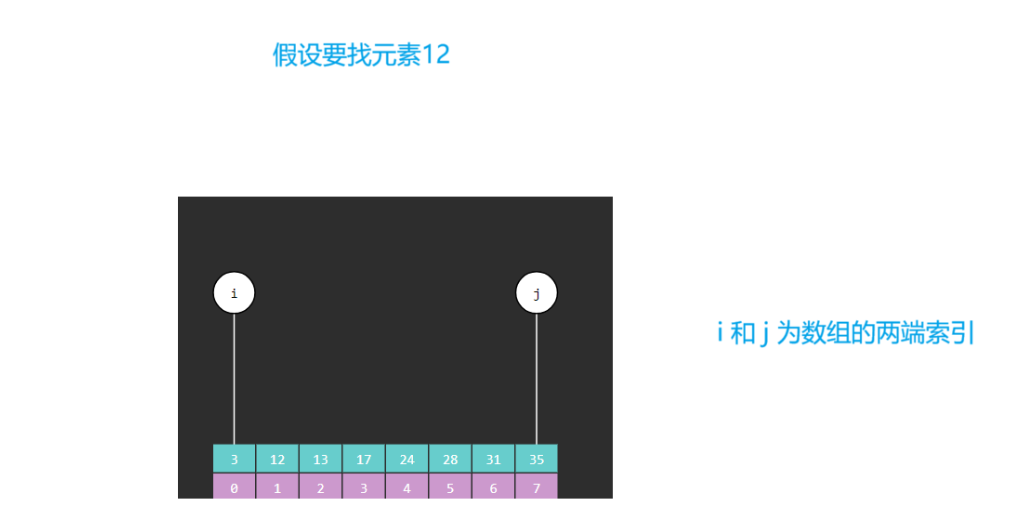
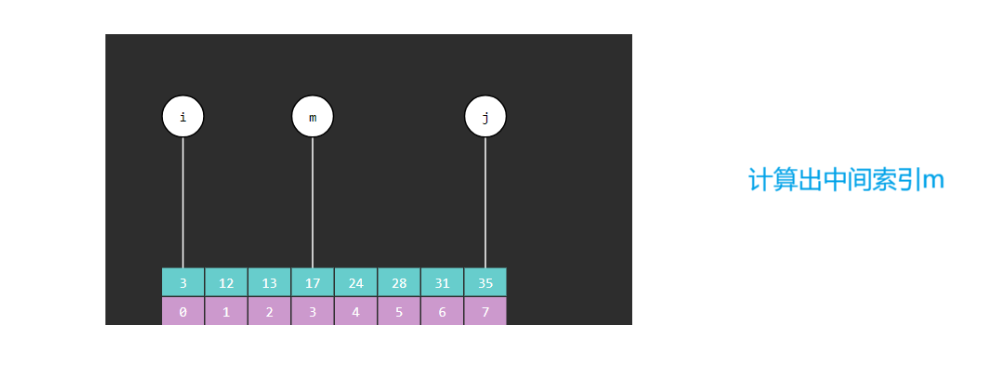
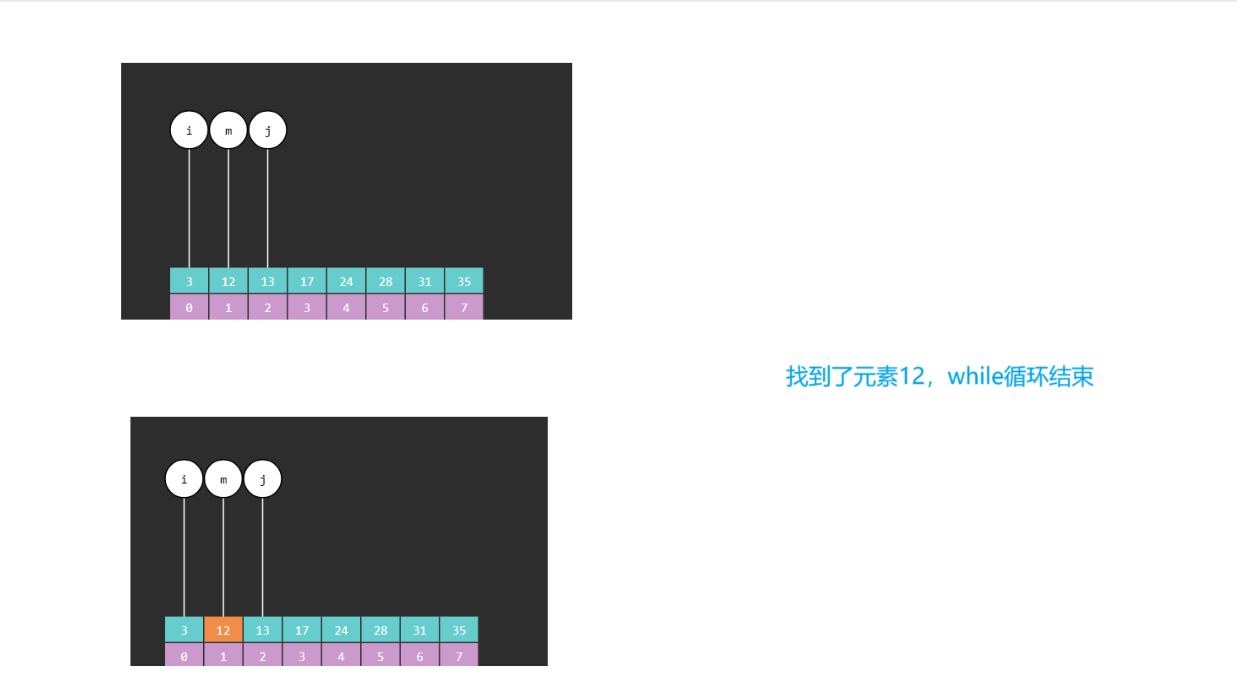
2.5 二分算法引发的问题

问题1：为什么是 i <= j ? 而不是 i < j呢?

因为当i == j，i，j 它们共同指向的元素也会参与比较
如果是i < j，意味着只有m指向的元素参与比较
这样可能会造成有些元素在数组中无法找到

问题2：(i + j) / 2 会产生的问题

因为当二分查找时，一个数组的元素足够的多时，
(i + j) / 2 会超过了整数的最大值。

给大家举个例子:

    @Test
    public void test4() {
        int i = 0;
        int j = Integer.MAX_VALUE - 1;
        System.out.println("整数最大值：" + Integer.MAX_VALUE);
        int m = (i + j) / 2;
        i = m + 1;
        System.out.println("i = " + i);
        System.out.println("j = " + j);
        System.out.println(i + j);
        // 出现这一现象的原因是，两数相加超过了整数的最大值
    }

为什么两个整数相加会出现负数呢？

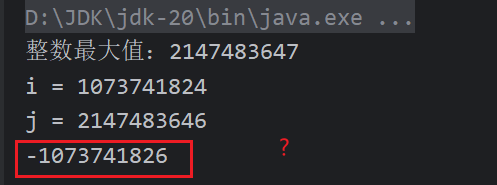
这是因为int类型的整数的最大值是2147483647，这两个数相加已经超出了一个int类型的数的最大值，所以会出现负数，又因为Java中没有无符号数，所有数都是有符号数，所以会出现这种情况

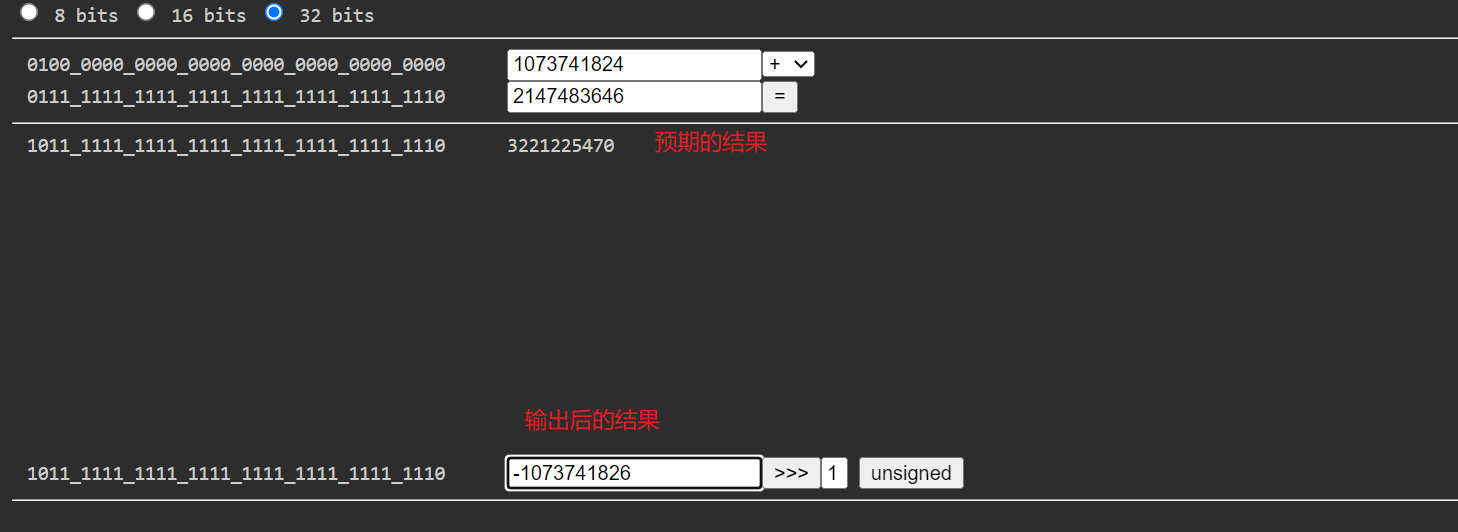
解决方法：采用无符号右移 >>> ，不保留符号位右移，高位补0

public static int binarySearchBasic(int[] a, int target) {
        int i = 0, j = a.length - 1;
        while (i <= j) {
            int m = (i + j) >>> 1;   // 这里与之前相比采用 >>> 来代替除号
            if (a[m] < target) {
                i = m + 1;
            }
            else if (target < a[m]) {
                j = m - 1;

            } else {
                return m;
            }
        }
        return -1;
    }

2.6 二分算法改良版

基于上面的二分计算基础版，还可以再改善

public static int binarySearchAlternative(int[] a, int target) {
        int i = 0, j = a.length;
        while (i < j) {
            int m = (i + j) >>> 1;
            if (a[m] < target) {
                // 此时i只是作为边界，而不参与运算
                i = m + 1;
            } else if (target < a[m]) {
                j = m;
            } else {
                return m;
            }
        }
        return -1;
    }

2.7 二分算法改良版解析

假如在数组中查找元素14，这时j指向的是数组的最后一个元素的索引加1，说的简单点，这个 j 指向的是边界

    public static int binarySearchAlternative(int[] a, int target) {
        int i = 0;
        int j = a.length;  // 与之前不同
        while (i < j) {  // 与之前不同
            int m = (i + j) >>> 1;
            if (a[m] > target) {
                j = m; // 与之前不同 
            } else if (a[m] < target) {
                i = m + 1;
            } else {
                return m;
            }
        }
        return -1;
    }

2.8 二分算法改良版图解

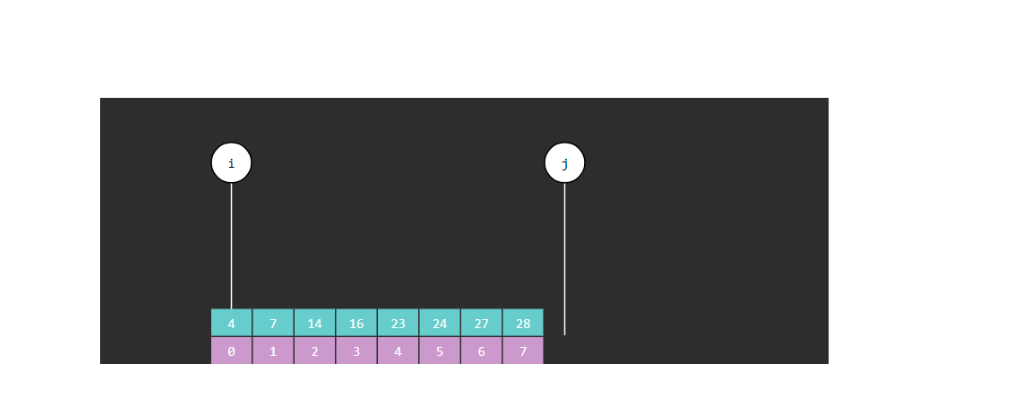
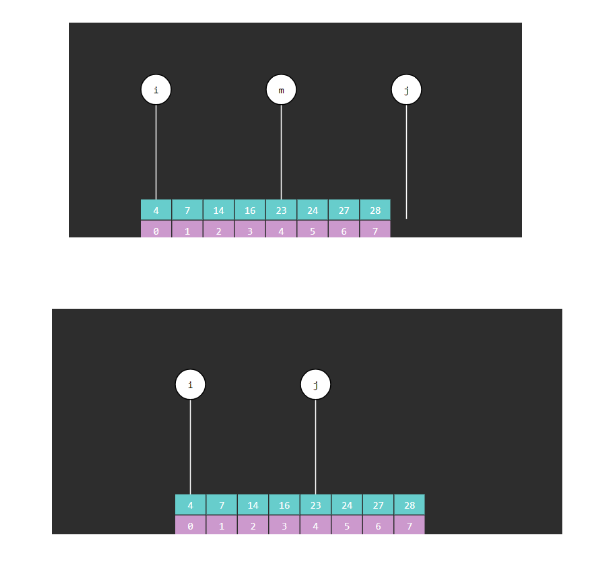
注意：此时j不参与运算

2.9 二分算法改良版注意事项

这里如果是 i<=j 并且查找的元素不在数组中会造成无限循环，前面也说过了，j指向的元素是边界，所以i=j时说明要查找的元素不在该数组中

    public static int binarySearchAlternative(int[] a, int target) {
        int i = 0, j = a.length;
        while (i <= j) {
            int m = (i + j) >>> 1;
            if (a[m] < target) {
                i = m + 1;
            } else if (target < a[m]) {
                j = m;
            } else {
                return m;
            }
        }
        return -1;
    }

3. 时间复杂度

3.1 时间复杂度的概念

时间复杂度是用来衡量：一个算法的执行，随数据规模增大，而增长的时间成本，利用大O来表示

• 如果运行时间是常数量级， 则用常数1表示
• 只保留间中的最高阶项
• 如果最高阶项存在， 则省去最高阶项前面的系数

3.2 线性查找的时间复杂度

    public static int linearSearch(int[] a, int target) {
        for (int i = 0; i < a.length; i++) {
            if (a[i] == target) {
                return i;
            }
        }
        return -1;
    }

要计算一个算法的时间复杂度，就要考虑该算法的最坏情况，假设该数组中有n个元素

int i = 0;    1次
i < a.length; n + 1次
i++           n次
a[i]==target  n次
return -1;    1次
3 * n + 3  

• 粗略认为每行代码执行时间是 $t$，假设 $n=4$ 那么总执行时间是 $(1+4+1+4+4+1)\ast t=15t$
• 可以推导公式为，$T=(3\ast n+3)t$

然后只保留最高阶项，再去掉最高阶项的系数
所以它的时间复杂度就是 $O(n)$

3.3 二分算法的时间复杂度

  考虑二分查找最坏的情况
  1 [2,3,4,5] 5 右侧没找到时，情况更差
  
  int i = 0,j = a.length-1;         2
  return -1;                        1
  元素个数              循环次数
  4-7                   3           floor(log_2(4))  = 2+1
  8-15                  4           floor(log_2(8))  = 3+1
  16-31                 5           floor(log_2(16)) = 4+1
  32-63                 6           floor(log_2(32)) = 5+1
  ....                 ...

  循环次数：floor(log_2(n)) + 1 , 我们把它看成L
  这里使用到了floor()方法，是因为当元素个数小于4的时就向下取整
  i<=j                  L+1
  int m = (i+j)>>>1     L
  a[m] < target         L
  target < a[m]         L
  i = m+1               L

  ((floor(log_2(n)) + 1) * 5) + 4     ->  最糟糕的情况

这里也是只保留最高项，然后去掉底数所以它的时间复杂度为 $log(n)$

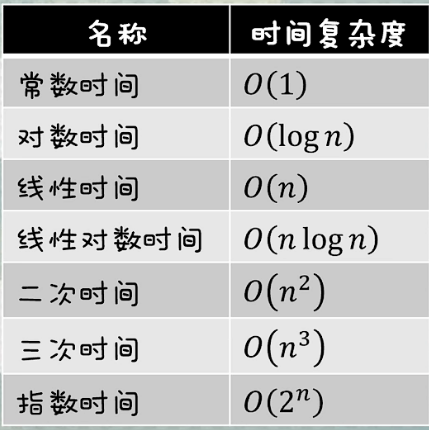
3.4 不同的时间复杂度对比

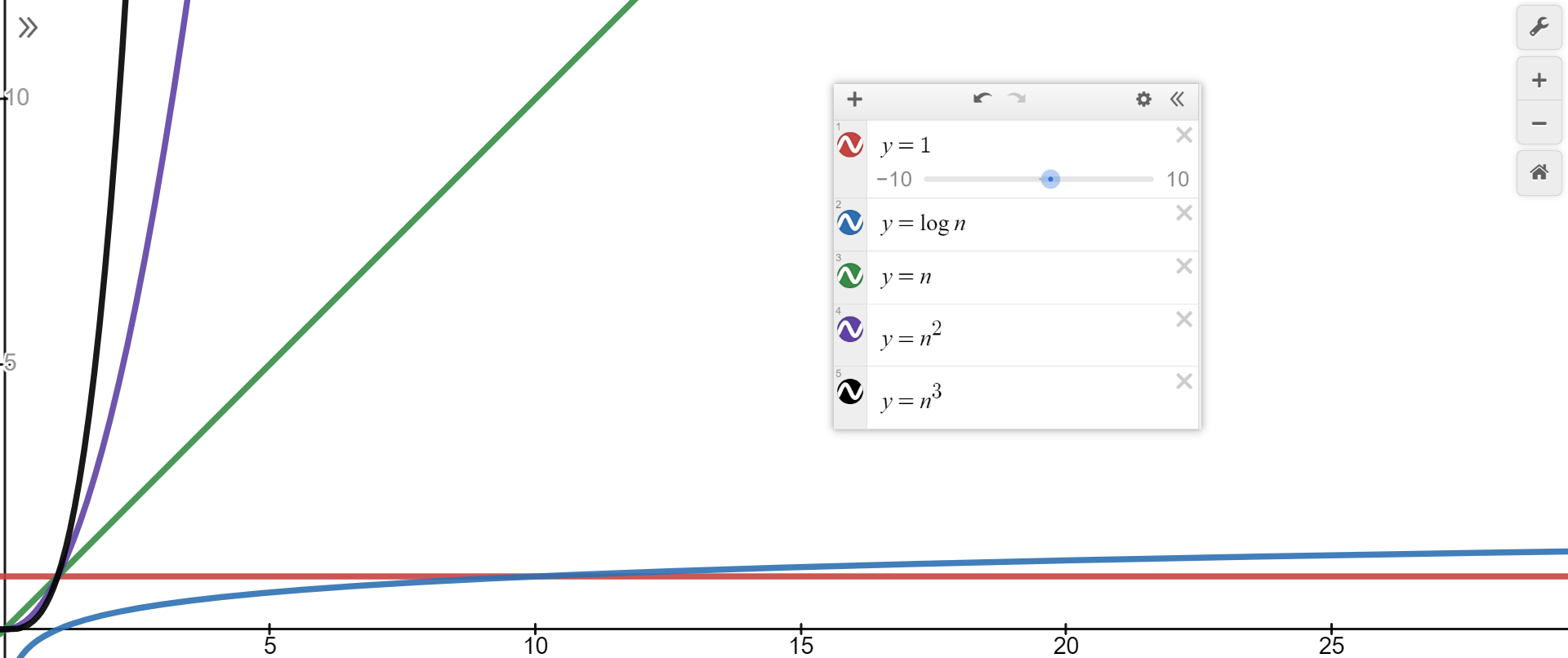
从上图中不难看出，当数据量足够大的时候，所消耗的时间为：$O(1)$ <$O(logn)$<$O(n)$<$O(n^2)$<$O(n^3)$

4. 空间复杂度

4.1 空间复杂度概念

与时间复杂度类似，一般也使用大 $O$ 表示法来衡量：一个算法执行随数据规模增大，而增长的额外空间成本

4.2 空间复杂度的计算

public static int binarySearchBasic(int[] a, int target) {
    int i = 0, j = a.length - 1;    
    while (i <= j) {               
        int m = (i + j) >>> 1;
        if(target < a[m]) {        
            j = m - 1;
        } else if (a[m] < target) { 
            i = m + 1;
        } else {                    
            return m;
        }
    }
    return -1;
}

这里因为是3个变量， i ，j , m ，一个int是4个字节
3 * 4B = 12B，同上面的时间复杂度，当它只有一个常数项时，它的空间复杂度为$O(1)$