内存中的数据是代码的基因,相当于人体中的DNA。
你看代码就是看内存,因此了解内存中的数据存储十分有必要。
内容较多,制作不易,多多点赞支持一下,我自己会总结科班和it培训班的精华共享。
下面的图片有代码和解释
内容大致分为int 型存储规则; 浮点型存储的规则及取数据的规则。最后拓展了浮点型单精度双精度的区别,小数转换二进制的方法。
图片可以复制下来,我已经空了很多空白地方,方便大家做自己的注释和总结!!!
这是我的笔记链接(已经开源),大家可以斧正
https://ebgx2518-my.sharepoint.com/personal/a4321_office36-5_nl/_layouts/15/Doc.aspx?sourcedoc={f29af28d-33a1-4667-900c-4f4c408abc0a}&action=edit&wd=target%28%E5%85%B3%E9%94%AE%E5%AD%97.one%7Cee32ba2c-c16a-48b9-8133-a5179e25cab4%2Fconst%7C61e3a7e2-5096-420b-9128-627e2369f8c3%2F%29&wdorigin=NavigationUrl

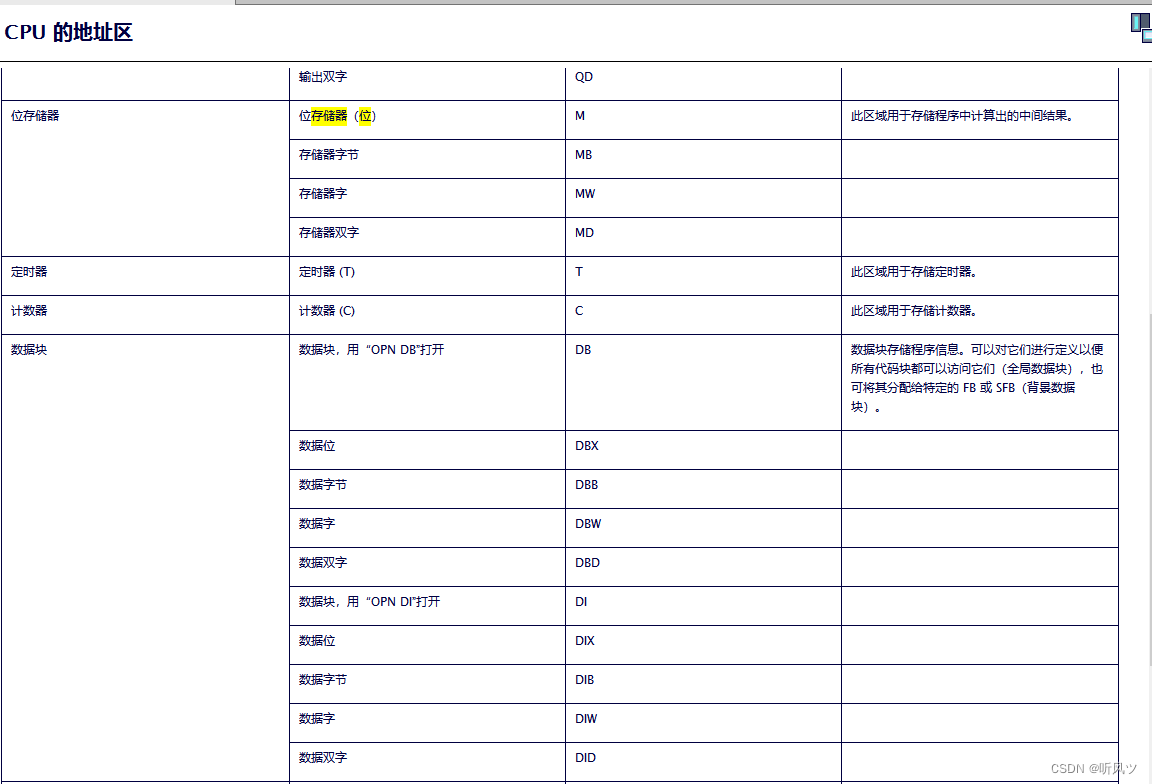
总结:int 型 4字节——32比特位(1个字节8个比特位),内存又分大小端存储,看电脑的怎么运行。显示为16进制,内存实际上是二进制。16进制是为了简洁观看。比如int a=10;——0000,0000,0000,0000,0000,0000,0000,1010
float 型 4字节——32比特位(1位存正负,8位存指数,23位),存数据的时候,先把小数化为二进制,二进制写出科学计数法,三大因子——(S,E,M)(正负,指数,有效数字)——正为0,负为1,写第一位,有效数字写最后,后面补0,最后写中间指数+127得到的8位二进制放在中间。
double 型 8字节——64比特(1位存正负,11位存指数,52位)其他和float单精度一样,就最后指数E+1023变成11位二进制有区别
下面拓展单精度双精度区别
1.精度:单精度使用32位(4字节)来存储浮点数,而双精度使用64位(8字节)。因此,双精度具有更高的精度,可以表示更大范围和更精确的数值。单精度通常提供7位有效数字,而双精度提供15-16位有效数字。
2.范围:单精度可以表示的范围约为±3.4 x 10^38,而双精度的范围约为±1.7 x 10^308。因此,双精度可以表示比单精度更大或更小的数值。
3.内存占用:由于双精度存储更多的位数,所以它占用的内存空间也更大。这意味着使用双精度数据类型时,需要更多的存储空间来存储相同数量的数据。
4.运算速度:单精度的运算速度通常会比双精度更快,因为它需要处理的位数较少。对于一些对精度要求不高的应用程序来说,单精度可以提供更高的计算效率。
怕初学者看不懂二进制转化细节
下面拓展小数转化二进制的基础知识?
将浮点数转换为二进制的过程通常涉及到两个主要步骤:将整数部分和小数部分分别转换为二进制,并应用浮点数的规范化表示。
下面是一个简单的示例,将浮点数13.625转换为二进制:
-
整数部分转换为二进制:将整数部分13除以2,并记录余数和商。重复这个步骤,直到商为0为止。将所得的余数从底部向上排列,即为整数部分的二进制表示。在这个示例中,13的二进制表示为1101。
-
小数部分转换为二进制:将小数部分0.625乘以2,并记录整数部分和小数部分。继续将小数部分乘以2,并重复这个过程,直到小数部分为0或达到所需的精度。将所得的整数部分从左到右排列,即为小数部分的二进制表示。在这个示例中,0.625的二进制表示为0.101。什么意思?0.625x2=1.25. 1.25x2=2.5
2.5x2=5.0—— 5的二进制101就是你的小数部分的二进制 -
结合整数部分和小数部分:将整数部分的二进制和小数部分的二进制组合在一起。在这个示例中,13.625的二进制表示为1101.101。
-
规范化表示:将二进制表示规范化,使得只有一个数字位数为1,即小数点的位置。通过将小数点向左或向右移动,调整整数部分和小数部分的位置。在这个示例中,可以将小数点向左移动3位,得到规范化的二进制表示为1.101101 × 2^3。
请注意,这只是一个简单的示例,实际的浮点数转换可能会更复杂,并涉及到更多的规则和约定。具体的浮点数表示也取决于所使用的编程语言和硬件平台。
谢谢你看到这里!制作不易,你的支持就是我更新的最大动力!