文章目录
- 二叉树的存储结构
- 二叉树的链式结构
- 二叉树的遍历
- 结点个数
- 寻找二叉树的某个结点
- 二叉树的层遍历
- 判断是否为完全二叉树
上一节 二叉树的堆链接入口
二叉树的存储结构
对于二叉树的存储,有两种存储方式:一种是顺序存储,另一种是链式存储。
顺序存储:在上一章的堆结构中,用到的就是顺序存储,它是用数字来存储数据,以二叉树的存储逻辑来存储的。一般只适用于完全二叉树,因为完全二叉树存储不会有空间浪费,而且可以根据数组的下标来找到对应的树节点;如果中间有节点是空的,那么或许需要用特殊的字符来表示该节点为空,这样做有些麻烦;
链式存储:对于二叉树来说,我们还是习惯使用链式的结构来存储;用结构体指针来表示左右孩子,分别为左右指针,表示可以走到左右孩子结点,用一个变量来存储数据;
typedef struct BinaryTree
{
int val;
struct BinaryTree* left;
struct BinaryTree* right;
}BTNode;
二叉树的链式结构
对于二叉树的链式结构,需要我们自己来手动创建;
BTNode* BuyTree(int x)
{
BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
if (newnode == NULL)
{
perror("Buynode fail");
exit(-1);
}
newnode->val = x;
newnode->left = newnode->right = NULL;
return newnode;
}
这步骤不难,只需要创建一个结点,将对应值赋值进去即可;
int main()
{
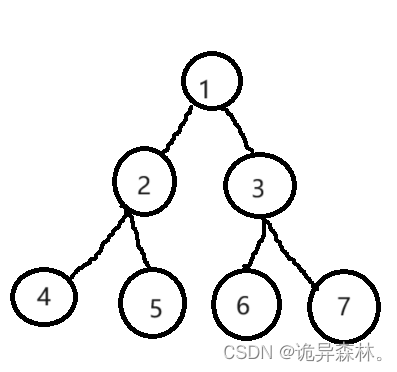
BTNode* node1 = BuyTree(1);
BTNode* node2 = BuyTree(2);
BTNode* node3 = BuyTree(3);
BTNode* node4 = BuyTree(4);
BTNode* node5 = BuyTree(5);
BTNode* node6 = BuyTree(6);
BTNode* node7 = BuyTree(7);
node1->left = node2;
node1->right = node3;
node2->left = node4;
node2->right = node5;
node3->left = node6;
node3->right = node7;
}
然后我们手动将每个结点联系起来。
二叉树的遍历
二叉树的遍历是实现二叉树结构访问的基本方式;那么一般是如何遍历结点的呢?
对于一颗二叉树的每个结点来说, 将自己看作是一个根节点,左右子树就是根节点的左孩子结点和右孩子结点;我们根据访问孩子结点,那么将孩子结点看作是根节点,它有它的左右孩子结点;
也就是说,在访问结点的过程中,我们可以将每个结点看作是当前的主体,利用递归的方式,将一个大的二叉树化解成每颗小的二叉树去解决,那么这样二叉树就完成了遍历;
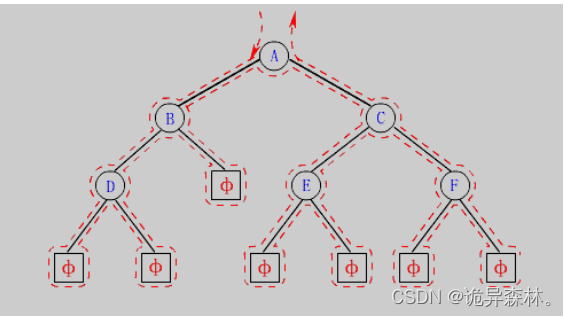
有规则这样规定,二叉树有三种递归方式的遍历:
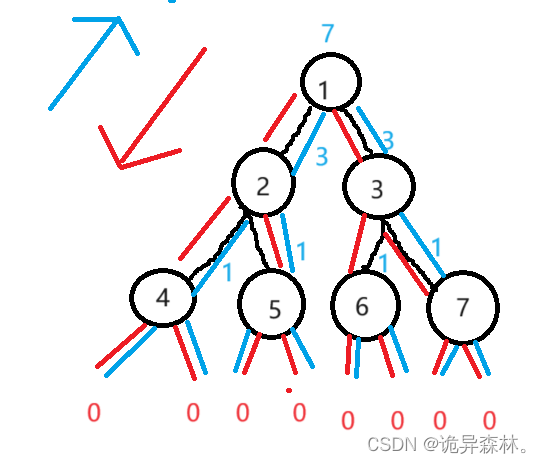
前序遍历(Preorder Traversal 亦称先序遍历):先访问根结点,再访问左结点后访问又结点;
中序遍历(Inorder Traversal):先访问左子树结点,再访问根结点后访问右结点;
后序遍历(Postorder Traversal):先访问左子树结点,再访问右子树结点,最后访问根节点;
前中后序遍历根据访问根节点的先后顺序来进行定义的;
上面讲这是一种递归遍历,那么我们就需要根据递归的方式来进行访问遍历。
递归新手入门链接入口
//前序
void PrevOrder(BTNode* root)
{
//终止条件
if (root == NULL)
{
return;
}
printf("%d ", root->val);
PrevOrder(root->left);
PrevOrder(root->right);
}
//中序
void InOrder(BTNode* root)
{
//终止条件
if (root == NULL)
{
return;
}
InOrder(root->left);
printf("%d ", root->val);
InOrder(root->right);
}
//后序
void PostOrder(BTNode* root)
{
//终止条件
if (root == NULL)
{
return;
}
PostOrder(root->left);
PostOrder(root->right);
printf("%d ", root->val);
}
对于前中后序遍历,大体的实现是一样的,只是顺序不同;每一次使用函数,就相当于进入下一个结点了,在函数里面的函数,他就是你的子结点,而当这个函数里面的函数开始实现时,那么他就是主体函数了;
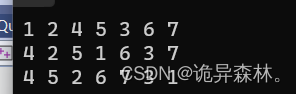
验证:
PrevOrder(node1);
printf("\n");
InOrder(node1);
printf("\n");
PostOrder(node1);
printf("\n");
结点个数
有了二叉树的遍历方式,那么就可以算出二叉树的结点数、叶子结点数、层数结点数 了。
//节点个数
int TreeSize(BTNode* root)
{
//终止条件
if (root == NULL)
{
return 0;
}
return TreeSize(root->left) + TreeSize(root->right) + 1;
}
//叶子节点个数
int LeafTree(BTNode* root)
{
//终止条件
if (root == NULL)
{
return 0;
}
else if (root->left == NULL && root->right == NULL)
{
return 1;
}
else
{
return LeafTree(root->left) + LeafTree(root->right);
}
}
//第k层节点数
int TreeLevel(BTNode* root, int k)
{
//终止条件
if (k == 1)
{
return 1;
}
//往下递归到k层
return TreeLevel(root->left, k - 1) + TreeLevel(root->right, k - 1);
}
结点个数:
将空结点返回为0,当某个结点当作是根结点,总结点数就是自己加上左右子树的结点数即可。
叶子结点:
叶子结点只需要在结点个数上改造一下就行,那么就需要对终止条件加以改造;根据叶子结点的概念,来进行设置条件。
k层结点:
我们可以先给出一个数,如第三层,那么我们可以推算一下,在第一层时,k3,第二层时,k2;第三层时,k==1;那么我们就知道了,只要当k等于1时,就到达了第k层了,根据这一条件,来完成条件的设置。
验证:
int size=TreeSize(node1);
printf("%d\n", size);
int leaf = LeafTree(node1);
printf("%d\n", leaf);
int k = TreeLevel(node1, 2);
printf("%d\n", k);

寻找二叉树的某个结点
对于寻找某个结点,只要某个结点的值与寻找值相同,就返回该结点;那么找不到的话就返回为空;
BTNode* BTFind(BTNode* root, int x)
{
//终止条件
if (root == NULL)
{
return NULL;
}
if (root->val == x)
{
return root;
}
//不符合条件时,
BTNode* ret = NULL;
ret = BTFind(root->left, x);
if (ret)
return ret;
ret = BTFind(root->right, x);
if (ret)
return ret;
return NULL;
}
对于一个符合条件想要返回的结点,我们要将它返回到第一个结点处,让最终返回的结点始终是它,那么我们就需要在递归函数返回时,对于每个结点都要判断是否符合条件,用一个常变量来暂时存储,然后只要符合条件就会进行返回该结点,不符合的话则会返回空,(这里的先后顺序很重要,符合条件的结点是最重要的,所以最后的返回结点是空,而在返回空结点前面的是返回正确的结点。
验证:
BTNode* x = BTFind(node1, 3);
printf("%d", x->val);
printf("\n");
答案:3
二叉树的层遍历
层遍历,顾名思义就是每一层从左向右依次遍历,那么这样的话用递归的方式就失效了;这里采用队列(先进先出)的方式来实现遍历。
void BTDestory(BTNode* root)
{
//终止条件
if (root == NULL)
{
return;
}
BTDestory(root->left);
BTDestory(root->right);
free(root);
}
void LevelOrder(BTNode* root)
{
if (root == NULL)
{
return ;
}
Quene Q;
QueneInit(&Q);
QuenePush(&Q, root);
while (!QueneEmpty(&Q))
{
BTNode* front = QueneFront(&Q);
printf("%d ", front->val);
if (front->left)
QuenePush(&Q, front->left);
if (front->right)
QuenePush(&Q, front->right);
QuenePop(&Q);
}
QueneDestory(&Q);
printf("\n");
}
这里先将根节点放入队列中,然后在循环中,每次循环将队头的取出读取,同时将队头的结点的左右孩子结点带进到队列里,利用这种方式,循环到队列为空时,就能完成层的遍历方式。
验证:
LevelOrder(node1);

判断是否为完全二叉树
int PerfectTree(BTNode* root)
{
Quene Q;
QueneInit(&Q);
if (root)
QuenePush(&Q, root);
while (!QueneEmpty(&Q))
{
BTNode* front = QueneFront(&Q);
if (front == NULL)
{
break;
}
QuenePush(&Q, front->left);
QuenePush(&Q, front->right);
QuenePop(&Q);
}
while (!QueneEmpty(&Q))
{
BTNode* Frt = QueneFront(&Q);
QuenePop(&Q);
if (Frt != NULL)
{
QueneDestory(&Q);
return 0;
}
}
QueneDestory(&Q);
return 1;
}
完全二叉树的概念是从上到下除了最后一层其他层都会布满结点,最后一层会从左开始布置结点,可以不布满。那么,我们可以利用层遍历的逻辑,来进行判断是否为完全二叉树。
在第一次循环中,只要遇到空结点,就停下来,如果此时队列不为空,那么就表示该树不是完全二叉树,反之。
验证:
k = PerfectTree(node1);
printf("%d", k);