【笔记】Splay 目录
- 简介
- 右旋
- 左旋
- 核心思想
- 操作
- a. Splay
- b. 插入
- c. 删除
- 信息的维护
- 例题
- AcWing 2437. Splay
- P3369 【模板】普通平衡树
简介
Splay 是一种平衡树,并且是一棵二叉搜索树(BST)。
它满足对于任意节点,都有左子树上任意点的值 < 当前节点的值 < 右子树上任意点的值。
优点:支持多种操作。
缺点:常数较大。
单次操作均摊复杂度 O ( log n ) O(\log n) O(logn)。
(注:关于 Splay 单次操作均摊复杂度的证明见 OI-Wiki)
Splay 基于旋转操作维护树的平衡。旋转分为左旋 (zag) 和右旋 (zig)。
旋转,即在保证平衡树中序遍历不变的前提下,改变整个树的深度。
右旋
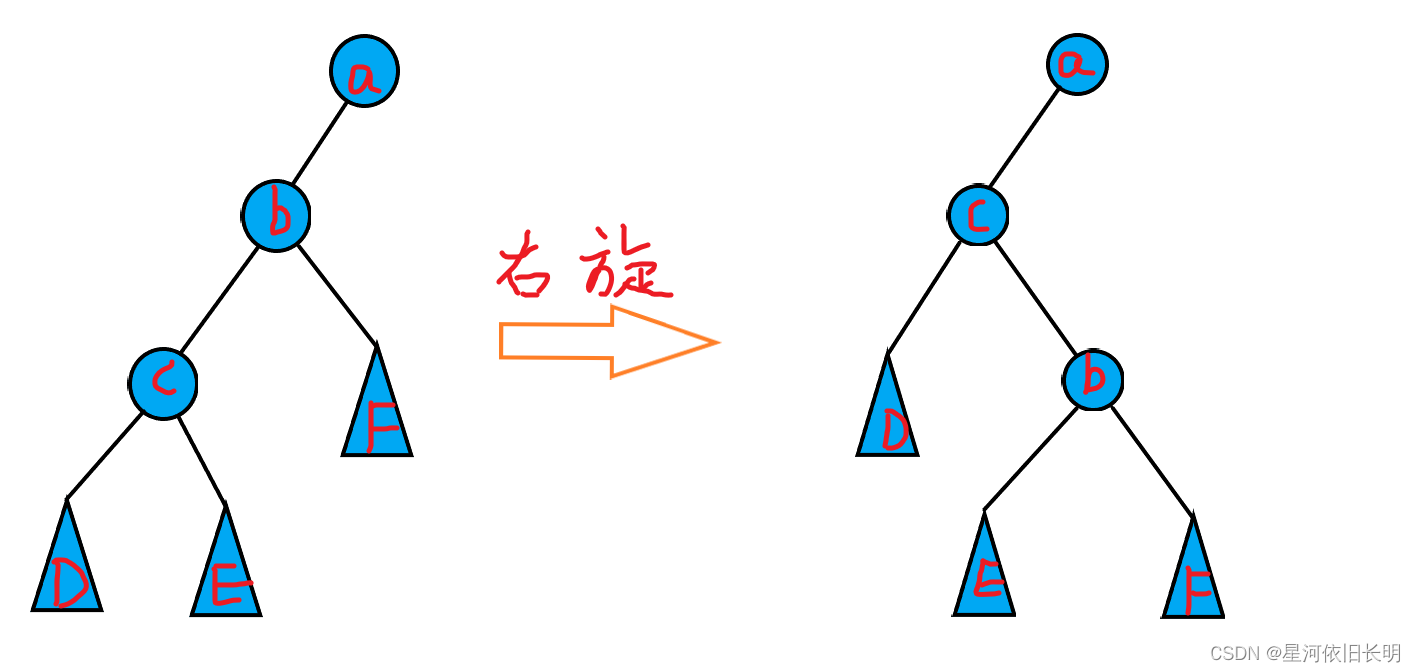
对于单次操作 zig(a) ,将节点
a
a
a 左儿子的左儿子(
c
c
c)接到
a
a
a 的左儿子处,将
c
c
c 的右儿子接到
b
b
b 的左儿子,将
c
c
c 的右儿子改为
b
b
b。
这样,我们完成了一次右旋操作,操作前后,
a
a
a 左子树的中序遍历都为 DcEbF。
左旋
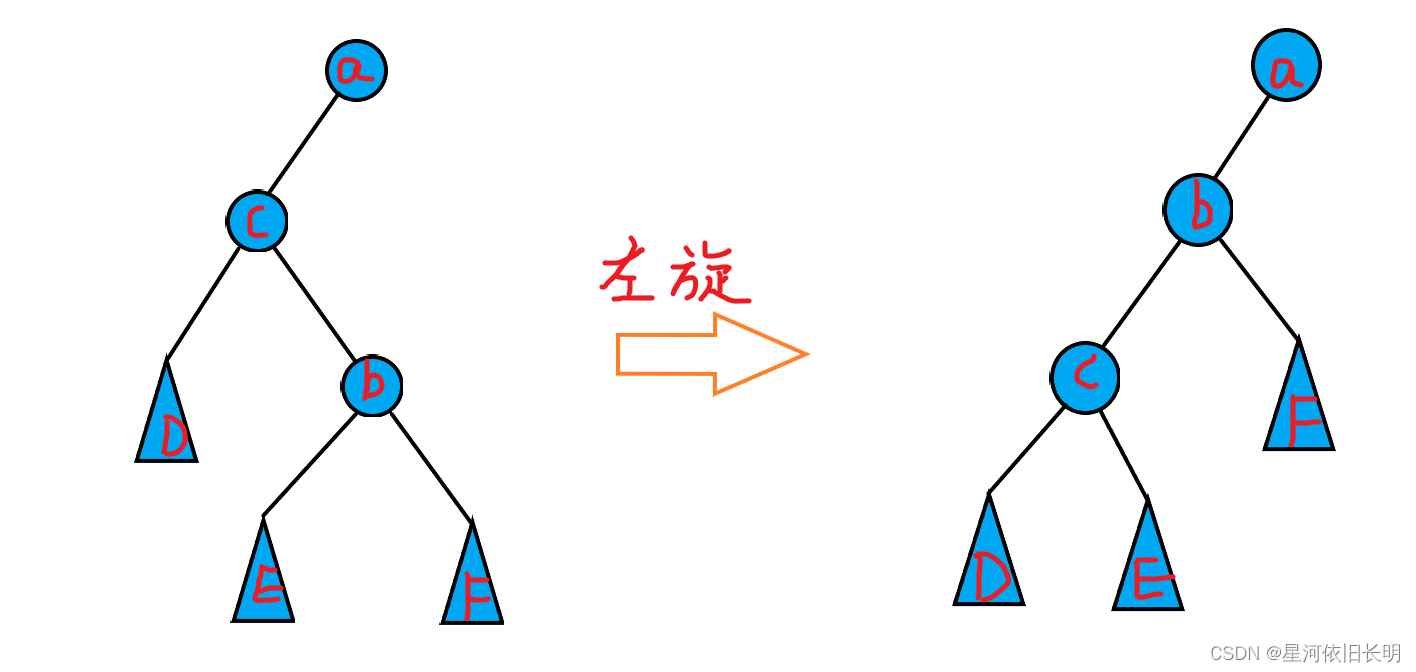
左旋即右旋的逆过程,将每一步反过来即可。
核心思想
每次操作之后,都将被操作的节点旋转至根节点。
这个和均摊时间复杂度有关。
操作
a. Splay
每次调用函数 splay(x, k) 表示把点
x
x
x 旋转至点
k
k
k 下方。
特别地,当调用 splay(x, 0) 时,表示把点
x
x
x 旋转至根节点。
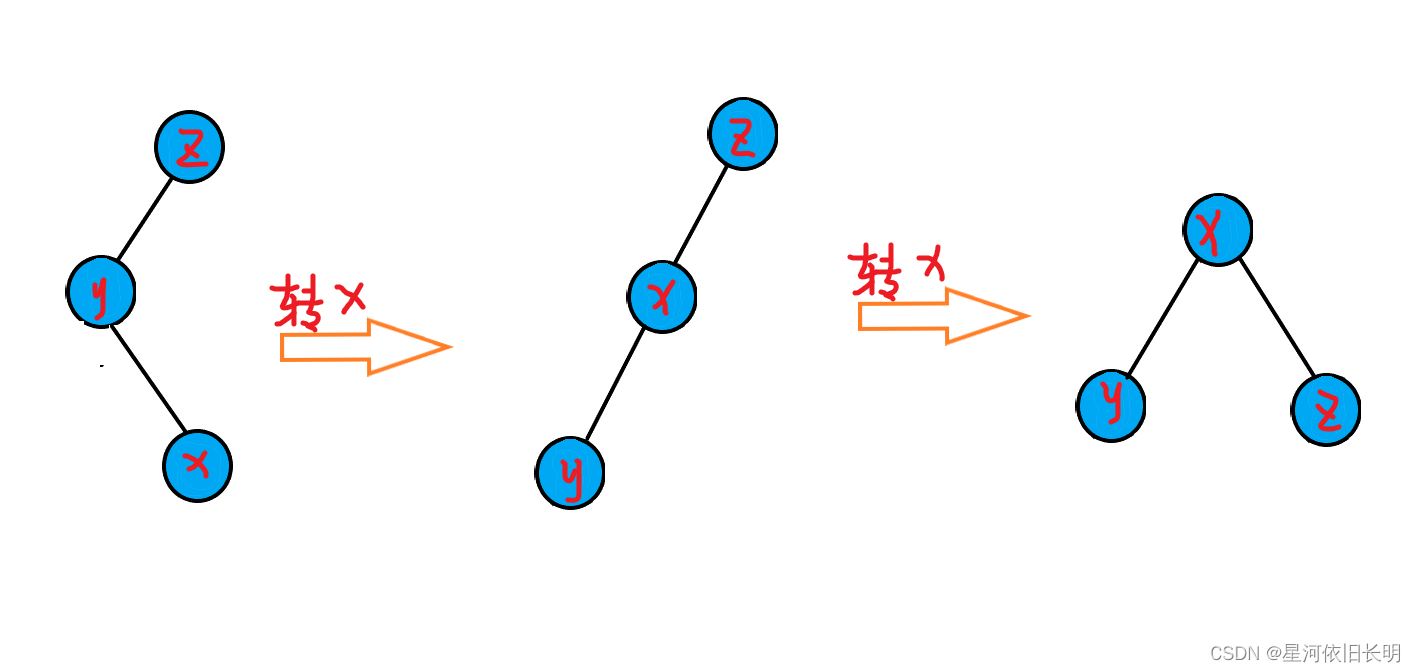
有两种情况:
- x , y , z x, y,z x,y,z 成一条链
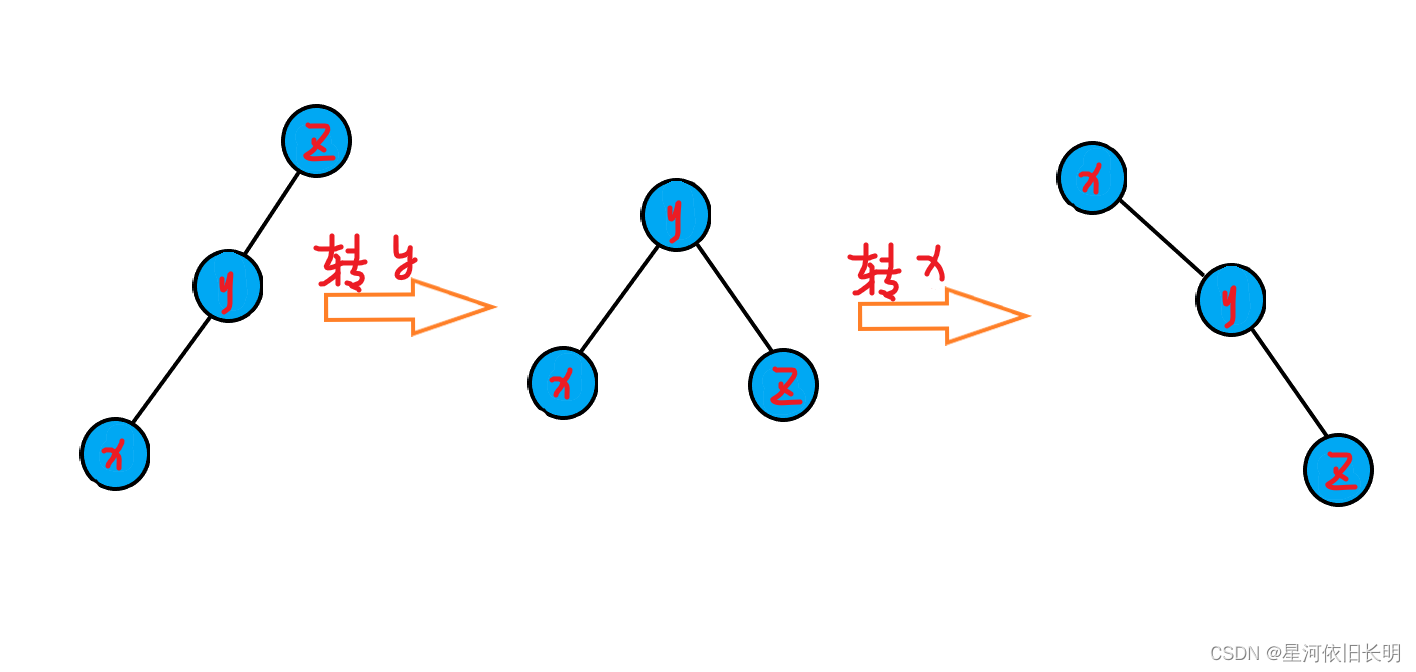
- x , y , z x,y,z x,y,z 不成一条链
b. 插入
- 根据 BST 性质,找到该元素所在位置并新建节点。插入后将该节点旋转至根节点。
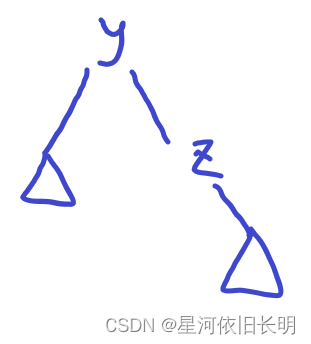
- 当要求将一个序列插到
y
y
y 的后面时:
- 找到 y y y 的后继 z z z。
- 将
y
y
y 转到根。(
splay(y, 0);) - 将
z
z
z 转到
y
y
y 的下方。(
splay(z, y);)由于 z > y z>y z>y,所以 z z z 是 y y y 的左儿子。 - 显然,此时将要插入的序列接到 z z z 的左儿子(∅)上即可。
c. 删除
- 删除一段区间
[
l
,
r
]
[l,r]
[l,r]。
- 分别找到 l l l 的前驱 p p p 和 r r r 的后继 q q q。
- 将 p p p 转到根节点。
- 将 q q q 转到 p p p 下方。由于 p < q p<q p<q,所以 q q q 是 p p p 的左儿子。
- 显然,要删除的区间就是点 p p p 的整个左子树。直接变没即可。


信息的维护
以模板题 AcWing 2437. Splay 为例。
本题要求我们进行区间翻转操作。
因此维护两个值:
- 以每个点为根节点的子树的大小
size。 - 区间翻转懒标记
flag。
和线段树一样,两个函数 pushup 和 pushdown 分别维护 size 和 flag。
本题的 Splay 保证中序遍历是当前序列的顺序,不一定满足 BST 性质。
例题
AcWing 2437. Splay
原题链接
本题仅是插入和翻转两个操作。翻转就是把这个区间所在子树的左右儿子分别翻转。
具体细节看代码。
struct Splay_Node
{
int s[2], p; // 左右儿子、父节点
int v, size, flag; // 值、子树大小、懒标
void init(int _v, int _p) // 初始化
{
v = _v, p = _p;
size = 1;
}
}tr[N];
int n, m;
int root, idx;
void pushup(int u) // 更新当前节点大小
{
tr[u].size = tr[tr[u].s[0]].size + tr[tr[u].s[1]].size + 1;
}
void pushdown(int u) // 将懒标记下传
{
if (tr[u].flag) // 如果当前节点有懒标
{
swap(tr[u].s[0], tr[u].s[1]); // 就交换左右儿子
tr[tr[u].s[0]].flag ^= 1; // 左儿子懒标记更新
tr[tr[u].s[1]].flag ^= 1; // 右儿子懒标记更新
tr[u].flag ^= 1; // 当前节点懒标记清空
}
}
void rotate(int x) // 旋转
{
int y = tr[x].p, z = tr[y].p; // 当前节点的父亲和祖父
int k = tr[y].s[1] == x, kk = tr[z].s[1] == y; // 0 -> left | 1 -> right
// 这里一个小技巧判断哪个儿子
tr[z].s[kk] = x, tr[x].p = z; // z的儿子改为x
tr[y].s[k] = tr[x].s[k ^ 1], tr[tr[x].s[k ^ 1]].p = y; // y的儿子改为x的反儿子
tr[x].s[k ^ 1] = y, tr[y].p = x; // x的反儿子变成y
pushup(y), pushup(x); // 更新节点x,y
}
void splay(int x, int k)
{
while (tr[x].p != k) // 如果k不是当前节点的父节点
{
int y = tr[x].p, z = tr[y].p; // 当前节点的父亲和祖父
if (z != k) // 如果k不是当前节点的祖父
if ((tr[y].s[1] == x) ^ (tr[z].s[1] == y)) rotate(x); // 不成链先转x
else rotate(y); // 成链先转y
rotate(x); // 最后都转一遍x
}
if (!k) root = x; // 如果当前x是根结点就更新root
}
void insert(int v) // 插入
{
int u = root, p = 0; // 当前节点和其父节点编号
while (u) p = u, u = tr[u].s[v > tr[u].v]; // 只要节点存在就往下找
// 后面那句意思是如果插入的值比当前节点小就去左子树,否则去右子树
u = ++ idx; // 动态开点编号
if (p) tr[p].s[v > tr[p].v] = u; // 如果u不是根结点就更新p的儿子为u
tr[u].init(v, p); // 初始化新的点u
splay(u, 0); // 将u整到根结点
}
int kth(int k) // 找第k小数
{
int u = root; // 从根结点开始找
while (tr[u].size >= k)
{
pushdown(u); // 找之前先下传懒标记
if (tr[tr[u].s[0]].size >= k) u = tr[u].s[0]; // 如果k比左子树小的话就去左子树
else if (tr[tr[u].s[0]].size + 1 == k) return splay(u, 0), u; // 如果刚好在当前点就返回
else k -= tr[tr[u].s[0]].size + 1, u = tr[u].s[1]; // 否则去右子树
}
return -1; // 找不到就返回-1
}
void output(int u) // 输出中序遍历"左-根-右"
{
pushdown(u); // 访问之前先下传
if (tr[u].s[0]) output(tr[u].s[0]); // 如果左子树存在就遍历左子树
if (tr[u].v >= 1 && tr[u].v <= n) printf("%d ", tr[u].v); // 根结点不是哨兵就输出根结点
if (tr[u].s[1]) output(tr[u].s[1]); // 如果右子树存在就遍历右子树
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 0; i <= n + 1; i ++ ) // 多加2哨兵防止越界
insert(i);
int l, r;
while (m -- )
{
scanf("%d%d", &l, &r);
l = kth(l), r = kth(r + 2); // 由于前面加了一个哨兵所以如果我们想要提取区间[l,r]就要以l和r+2分割
splay(l, 0), splay(r, l); // 将l转到根节点,将r+2转到根节点下方
tr[tr[r].s[0]].flag ^= 1; // 把r+2的左子树打上懒标记
}
output(root);
return 0;
}
P3369 【模板】普通平衡树
原题链接
您需要写一种数据结构(可参考题目标题),来维护一些数,其中需要提供以下操作:
- 插入 x x x 数
- 删除 x x x 数(若有多个相同的数,应只删除一个)
- 查询 x x x 数的排名(排名定义为比当前数小的数的个数 + 1 +1 +1 )
- 查询排名为 x x x 的数
- 求 x x x 的前驱(前驱定义为小于 x x x,且最大的数)
- 求 x x x 的后继(后继定义为大于 x x x,且最小的数)
- 插入:根据 BST 的性质,找到这个值所在的节点。如果该节点存在,则将 cnt + 1 \text{cnt}+1 cnt+1。如果不存在就新建一个节点。
- 删除:找到这个值的前驱 prev \text{prev} prev 和后继 next \text{next} next(节点编号),将 prev \text{prev} prev 转到根节点,将 next \text{next} next 转到 prev \text{prev} prev 下方。如果 next \text{next} next 左儿子 cnt > 1 \text{cnt}>1 cnt>1 则将 cnt − 1 \text{cnt}-1 cnt−1,否则直接删除左儿子。
- 根据数值找排名:将该数值对应的节点转到根节点,然后返回左子树的大小 + 1 +1 +1。
- 根据排名找数值:从根结点开始找,如果 k k k 比左子树小的话就去左子树,如果刚好在当前点就把这个点转上去并返回,否则去右子树。
- 求前驱:根据 BST 性质先找出它的位置转到根节点。如果这个值不存在即根节点值小于输入值,则返回根节点值。否则返回根结点左子树的最右儿子。
- 求后继:根据 BST 性质先找出它的位置转到根节点。如果这个值不存在即根节点值大于输入值,则返回根节点值。否则返回根结点右子树的最左儿子。
struct Node
{
int size, cnt, v;
int p, s[2];
void init(int _v, int _p)
{
v = _v, p = _p;
size = 1;
}
}tr[N];
int n;
int root, idx;
void pushup(int x) // 更新子树大小
{
tr[x].size = tr[tr[x].s[0]].size + tr[tr[x].s[1]].size + tr[x].cnt; // 注意因为值可以重复,所以加cnt
}
void rotate(int x) // 旋转
{
int y = tr[x].p, z = tr[y].p;
int k = tr[y].s[1] == x;
tr[z].s[tr[z].s[1] == y] = x, tr[x].p = z;
tr[y].s[k] = tr[x].s[k ^ 1], tr[tr[x].s[k ^ 1]].p = y;
tr[x].s[k ^ 1] = y, tr[y].p = x;
pushup(y), pushup(x);
}
void splay(int x, int k) // 这个可以去翻上面的注释
{
while (tr[x].p != k)
{
int y = tr[x].p, z = tr[y].p;
if (z != k)
if ((tr[y].s[1] == x) ^ (tr[z].s[1] == y)) rotate(x);
else rotate(y);
rotate(x);
}
if (!k) root = x;
}
void upper(int v) // 根据BST性质找值v所在的节点并转到根节点
{
int u = root; // 从根结点开始
while (tr[u].s[v > tr[u].v] && tr[u].v != v) // 如果值比当前节点小就去左子树,否则去右子树
u = tr[u].s[v > tr[u].v];
splay(u, 0); // 找到之后将这个节点转到根节点
// 如果这个值不存在,则显然会返回这个值前驱或后继所在的节点
}
int get_prev(int v) // 找前驱
{
upper(v); // 转到根节点
if (tr[root].v < v) return root; // 如果这个值不存在且根结点值小则根节点就是前驱
int u = tr[root].s[0]; // 从左子树开始搜
while (tr[u].s[1]) u = tr[u].s[1]; // 左子树最右面
return u;
}
int get_next(int v) // 找后继
{
upper(v); // 转到根节点
if (tr[root].v > v) return root; // 如果这个值不存在且根结点值大则根结点就是后继
int u = tr[root].s[1]; // 从右子树开始搜
while (tr[u].s[0]) u = tr[u].s[0]; // 右子树最左面
return u;
}
int get_rank_by_val(int v) // 根据数值找排名
{
upper(v); // 转到根节点
return tr[tr[root].s[0]].size + 1; // 左子树大小+1
}
int get_val_by_rank(int k) // 根据排名找数值
{
int u = root;
while (tr[u].size >= k)
{
if (tr[tr[u].s[0]].size >= k) u = tr[u].s[0];
else if (tr[tr[u].s[0]].size + tr[u].cnt >= k) return splay(u, 0), tr[u].v; // 记得把当前点转上去
else k -= tr[tr[u].s[0]].size + tr[u].cnt, u = tr[u].s[1];
}
return -1;
}
void insert(int v) // 插入一个值
{
int u = root, p = 0;
while (u && tr[u].v != v) p = u, u = tr[u].s[v > tr[u].v];
if (u) tr[u].cnt ++ ; // 如果这个点已经存在就把cnt+1
else
{
u = ++ idx; // 否则新建一个点
if (p) tr[p].s[v > tr[p].v] = u; // 如果新建的不是根结点就更新其父节点的儿子指针
tr[u] = {1, 1, v, p}; // 初始化
}
splay(u, 0);
}
void remove(int v) // 移除一个值
{
int prev = get_prev(v), next = get_next(v); // 找出前驱和后继
splay(prev, 0), splay(next, prev); // 将前驱转到根节点,将后继转到前驱下方
int w = tr[next].s[0]; // 后继的左儿子是要删除的值
if (tr[w].cnt > 1) tr[w].cnt -- , splay(w, 0); // 如果不止一个就把cnt-1然后转上去
else tr[next].s[0] = 0, splay(next, 0); // 否则把next左儿子指针置空然后把后继转上去
}
void output(int u)
{
if (tr[u].s[0]) output(tr[u].s[0]);
if (tr[u].v != -INF && tr[u].v != INF) printf("%d ", tr[u].v);
if (tr[u].s[1]) output(tr[u].s[1]);
}
int main()
{
int op, x;
insert(INF), insert(-INF); // 为防止出界整两个哨兵
scanf("%d", &n);
while (n -- )
{
scanf("%d%d", &op, &x);
switch (op)
{
case 1: insert(x); break;
case 2: remove(x); break;
case 3: printf("%d\n", get_rank_by_val(x) - 1); break; // 由于有哨兵,所以排名-1
case 4: printf("%d\n", get_val_by_rank(x + 1)); break; // 由于有哨兵,所以输入+1
case 5: printf("%d\n", tr[get_prev(x)].v); break; // 由于找前驱返回的是下标
case 6: printf("%d\n", tr[get_next(x)].v); break; // 所以输出数值
}
}
return 0;
}
最后,如果觉得对您有帮助的话,点个赞再走吧!