跳马问题

题目背景

在爱与愁的故事第一弹第三章出来前先练练四道基本的回溯/搜索题吧……

题目描述

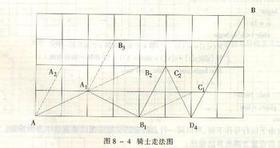
中国象棋半张棋盘如图 $1$ 所示。马自左下角 $(0,0)$ 向右上角 $(m,n)$ 跳。规定只能往右跳，不准往左跳。比如图 $1$ 中所示为一种跳行路线，并将路径总数打印出来。

输入格式

只有一行：两个数 $n$，$m$。

输出格式

只有一个数：总方案数 $total$。

样例 #1

样例输入 #1

4 8

样例输出 #1

37

提示

对于 $100\%$ 的数据：$n,m\le 18$

---

思路

马只能走日字形，即向右跳两格再向上或向下跳一格，或向下跳两格再向左或向右跳一格。

在 dfs 函数中，采用递归的方式进行搜索，每次尝试从当前位置 (x,y) 跳跃到下一个位置 (x+rx[i],y+ry[i])，其中 rx 和 ry 数组分别存储了四个方向的跳跃规则。

在跳跃到下一个位置之后，需要判断是否越界。如果越界了，就返回上一层递归；如果到达了终点 (m,n)，就将 ans 加一，并返回上一层递归。

注意：

1. 输入是 n、m ，终点是（m，n）。
2. 只能往右跳，不准往左跳。
3. 需要判断是否越界：x不能超过m，y不能超过n。

---

AC代码

#include <iostream>
#define AUTHOR "HEX9CF"
using namespace std;

const int N = 55;

int n, m;
int ans;

const int rx[4] = {1, 2, 1, 2};
const int ry[4] = {2, 1, -2, -1};

void dfs(int x, int y)
{
    if (x > m || y < 0 || y > n)
    {
        return;
    }
    if (x == m && y == n)
    {
        ans++;
        return;
    }
    // cout << x << " " << y << endl;
    for (int i = 0; i < 4; i++)
    {
        dfs(x + rx[i], y + ry[i]);
    }
}

int main()
{
    ans = 0;
    cin >> n >> m;
    dfs(0, 0);
    cout << ans << endl;
    return 0;
}