🤵‍♂️ 个人主页: @AI_magician
📡主页地址： 作者简介：CSDN内容合伙人，全栈领域优质创作者。
👨‍💻景愿：旨在于能和更多的热爱计算机的伙伴一起成长！！🐱‍🏍
🙋‍♂️声明：本人目前大学就读于大二，研究兴趣方向人工智能&硬件（虽然硬件还没开始玩，但一直很感兴趣！希望大佬带带）

【深度学习 | 非线性拟合】那些深度学习路上必经的核心概念，确定不来看看？ （一） 作者： 计算机魔术师 版本： 1.0 （ 2023.8.27 ）

---

摘要： 本系列文章内容都是博主用心学习收集所写，欢迎大家三联支持！本系列会一直更新，核心概念系列会一直更新！欢迎大家订阅

本文是博主在解决朋友一个问题 —— 如何纯Python实现仅对任意六个点六个点进行非线性拟合，以三项式非线性拟合（一元），且存在不等式约束，一阶导数恒大于0（这个很重要,这个约束实现细节是魔鬼）。本文从开始解决问题到解决问题流程撰写，希望可以帮助到你！

该文章收录专栏
[✨— 《深入解析机器学习：从原理到应用的全面指南》 —✨]

梯度下降算法

根据六个点的非线性问题，我的第一个思路就是梯度下降算法，于是我封装了整个梯度下降算法流程代码如下

#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Time    : 2023/8/30 16:03
# @Author  : AI_magician
# @File    : 原生Python实现（梯度下降算法）误差51 _ 11 .py
# @Project : PyCharm
# @Version : 1.0,
# @Contact : 1928787583@qq.com",
# @License : (C)Copyright 2003-2023, AI_magician",
# @Function: Use original python to fix a three project curve


import matplotlib.pyplot as plt
from typing import List
import numpy as np


def find_square_root(number, epsilon):
    guess = number / 2  # 初始猜测为number的一半

    while abs(guess * guess - number) > epsilon:
        guess = (guess + number / guess) / 2

    return guess


number = 16
epsilon = 1e-6


class Trinomials:
    parameter = [1., 1., 1., 1.]  # init parameter (which can use np.random to generate)
    learning_rate = 0.00005

    # m_min = 0
    # m_max = 100
    # max_iterations = 50

    def __init__(self):
        pass

    @staticmethod
    def func_polynomial(x, b: List[float]):
        # 三项式函数
        return b[0] * x ** 3 + b[1] * x ** 2 + b[2] * x + b[3]

    @staticmethod
    def const_1st_derivative(x, b: List[float]):
        """
        :param x: Single
        :param b: List
        :return:  first derivative
        """
        # 一阶导数
        return 3 * b[0] * x ** 2 + 2 * b[1] * x + b[2]

    def gradient_descent_with_constraints(self, x, y, b):
        """
        :param x: Single Float
        :param y: Single Float
        :param b: List Float
        :return: Parameter
        :description: gradient descent algorithm
        """
        # for i in range(max_iterations):
        # 计算关于每个参数的偏导数（梯度）
        gradients = [
            # 2 * (self.func_polynomial(x, b) - y) * 3 * b[0] * x ** 2,
            # 2 * (self.func_polynomial(x, b) - y) * 2 * b[1] * x,
            # 2 * (self.func_polynomial(x, b) - y) * b[2] * x,
            # 2 * (self.func_polynomial(x, b) - y)]
            2 * (self.func_polynomial(x, b) - y) * x ** 3,
            2 * (self.func_polynomial(x, b) - y) * x ** 2,
            2 * (self.func_polynomial(x, b) - y) * x,
            2 * (self.func_polynomial(x, b) - y)]
        # print("梯度：", gradients)

        # def constraints():
        b_update = [0] * len(b)
        for i, b_i in enumerate(b):
            b_update[i] = b_i - gradients[i] * self.learning_rate
        # self.learning_rate *= 0.3
        if self.const_1st_derivative(x, b_update) > 0:
            return b_update
        else:
            return b

    def fit(self, x, y, m_min=0, m_max=100, learning_rate=0.1, max_iterations=5000):
  
        for index in range(10000):
            for i in range(len(x)):
                self.parameter = self.gradient_descent_with_constraints(x[i], y[i], self.parameter)
                print("参数", self.parameter)
            # self.learning_rate *= 0.03
            # print(self.learning_rate)
        return self.parameter

    def error_square(x_a, y_a, coef_a):
        total_err = sum((Trinomials.func_polynomial(xi, coef_a) - yi) ** 2 for xi, yi in zip(x_a, y_a))

        return total_err


if __name__ == "__main__":
    # x_a = [19614.84, 12378.01, 5522.57, 3214.22, 1799.61, 894.12]
    # y_a = [44.85, 44.87, 43.75, 32.05, 27.37, 25.14]
    x_a = [5631.53, 3525.00, 1510.55, 868.94, 485.06, 242.01]
    y_a = [44.62, 44.24, 43.18, 41.39, 36.60, 28.84]
    x_a = np.log10(x_a)
    trinomials = Trinomials()
    coef_a = Trinomials.fit(trinomials, x=x_a, y=y_a)

    print("-----------for trinomials function --------------------")

    print(f"coefficients: {coef_a}")

    print(f"total error for six points is : {Trinomials.error_square(x_a, y_a, coef_a)}")

    p = np.poly1d(coef_a)

    # # 创建x轴上的一系列点，用于绘图
    x_plot = np.linspace(min(x_a), max(x_a), 400)

    # # 使用拟合的多项式计算这些点的y值
    y_plot = p(x_plot)

    # # 绘图
    plt.figure(figsize=(10, 6))
    # plt.scatter(x_a, y_a, color='red', label='Data points')
    plt.scatter(x_a, y_a, color='blue', label='Data points')

    plt.plot(x_plot, y_plot, label='polynomial fit')
    plt.xlabel('X')
    plt.ylabel('Y')
    plt.legend()
    plt.show()

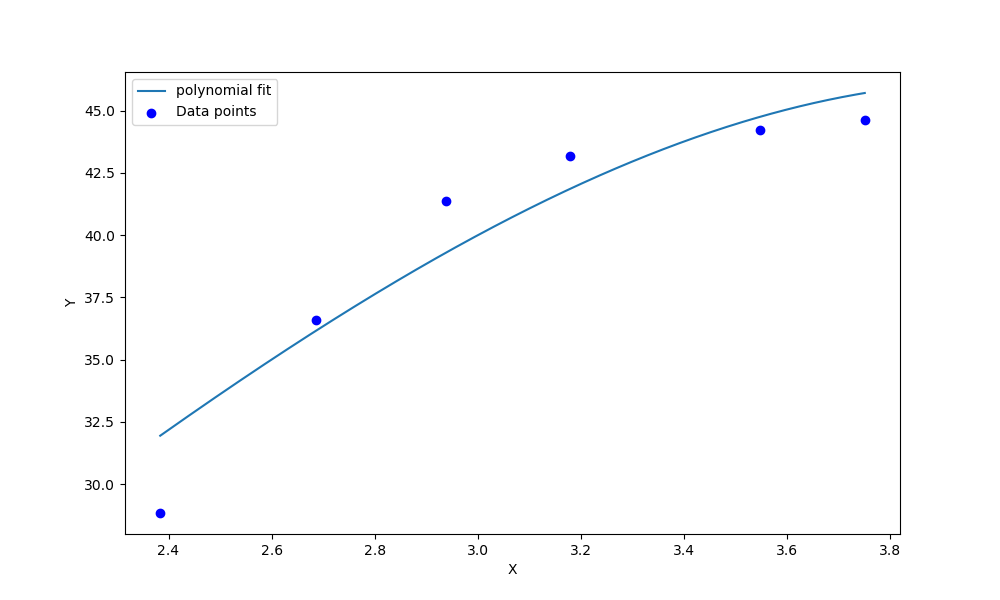
这个算法整体思路先用log进行数据标准化，根据目标函数和约束条件进行代码迭代

$$\begin{gathered} f(x)=a\cdot x^3+b\cdot x^2+c\cdot x+d \\ g(x)=f^{\prime }(x)=3a\cdot x^2+2b\cdot x+c>0 \end{gathered}$$

其次通过迭代多次，拟合曲线，但是数据太少了，拟合效果很差，误差很大(11)。尝试了一些技巧，考虑是数据太少了，梯度下降算法本身难以拟合，之前的文章有讲解过 ——》 【机器学习】浅谈正规方程法&梯度下降

SLSQP算法

在查阅大量文献后，发现改问题适合是非线性问题带有约束条件的优化问题（我几乎没学过优化算法，看来得补补了🤦‍♂️），在使用SLSQP算法能够非常有效的拟合。以下是SLSQP算法的原理详解。

SLSQP（Sequential Least Squares Programming）连续最小二乘法算法是一种优化算法，用于求解带有约束条件的非线性优化问题。它通过迭代地寻找目标函数在约束条件下的最小值。

下面是SLSQP算法的数学公式理论推导，并给出一个简单案例示范推导过程。

假设我们有一个非线性约束优化问题，目标是最小化某个函数f(x)，同时满足一组等式约束g(x) = 0和不等式约束h(x) >= 0。其中x是待求解的变量向量。

1. 线性模型近似
   首先，在每次迭代中，SLSQP算法会对目标函数和约束函数进行线性近似处理。这可以通过在当前点处计算目标函数和约束函数的梯度（Jacobian矩阵）来实现。

2. 无约束最小二乘问题
   接下来，将原始非线性约束优化问题转换为一个无约束最小二乘问题。具体地说，我们引入拉格朗日乘子λ和μ来表示等式和不等式条件的惩罚项。
   定义拉格朗日函数
   $$L(x,\lambda ,\mu )=f(x)+{\lambda }^T\ast g(x)+{\mu }^T\ast h(x)$$

   其中${}^T$表示向量转置操作。

3. 迭代更新规则
   通过求解无约束最小二乘问题，我们可以得到每次迭代的更新规则。在SLSQP算法中，这个规则是由以下两个方程组给出：
   a. 一阶必要条件：
   $$\nabla L(x,\lambda ,\mu )=\nabla f(x)+J_g^T\ast \lambda +J_h^T\ast \mu =0$$
   其中$J_g$和$J_h$分别表示等式和不等式约束函数的雅可比矩阵。
   b. 约束满足性条件：$g(x)=0$ 和$ h(x) >= 0$

4. 迭代过程
   根据上述更新规则，在每次迭代中，我们需要计算目标函数、梯度、约束函数以及它们的雅可比矩阵，并使用数值优化方法（如牛顿法或拟牛顿法）来求解更新方程。

现在让我们通过一个简单案例来演示SLSQP算法的推导过程，下面将详细介绍SLSQP算法的理论推导以及如何使用该算法求解多项式参数。

SLSQP算法主要分为两个阶段：搜索阶段和修正阶段。在搜索阶段中，通过构造一个次序二次规划模型来寻找可行点；在修正阶段中，在每次迭代时进行局部搜索以获得更好的近似值，并更新当前估计点。

具体推导过程如下：

1. 初始化：选择初值 $x_0$ ，并设定停止准则。

2. 进入主循环：

   • 计算梯度向量 $\nabla f_k(x_k)$ ，其中 $k$ 表示当前迭代次数。

   • 若 $||\nabla f_k(x_k)||<ϵ$ ，其中 $ϵ$ 是预设的停止准则，则停止算法并得到近似解 $x^{\ast }$ 。

   • 构造一个次序二次规划模型：
     $$\begin{array}{rl}& \text{minimize}q(x)=f_k(x)+g_k^T(x-x_k)+\frac{1}{2}(x-x_k{)}^T{B}_k(x-x_k)\\ & \text{subject to}{A}_{eq}(x-x_0)=0,\\ & g_i(x)\ge 0,i=1,\dots ,m\end{array}$$

     其中，$B_k$ 是正定对称矩阵，用于近似Hessian矩阵的逆；$A_{eq}$ 是等式约束的雅可比矩阵。

   • 求解上述二次规划问题，得到修正方向 $\Delta x$ 。

   • 计算步长 $\alpha$ ，使得目标函数在搜索方向上有足够下降：$\alpha =min(1,r)$ ，其中
     $$r=\max ({\beta }_s,r_t),$$

     $${\beta }_s={\left(\frac{\partial f}{\partial x}\right)}^T(\Delta x/s),$$

     $$r_t={\left(\frac{\partial g}{\partial x}\right)}^T(\Delta x/t),$$

     其中，$s$ 和 $t$ 是正的比例因子。

   • 更新估计点：$x_{k+1}=x_k+\alpha \Delta x$

   • 返回主循环。

根据以上推导，我们可以使用SLSQP算法求解多项式参数。首先，将目标函数和约束条件表示为数学形式：

$$\begin{gathered} f(x)=a\cdot x^3+b\cdot x^2+c\cdot x+d \\ g(x)=f^{\prime }(x)=3a\cdot x^2+2b\cdot x+c>0 \end{gathered}$$

然后，通过实现上述算法步骤，并设置合适的初值、停止准则、比例因子等参数进行迭代优化即可求得多项式的参数解。

通过求解上述方程组，我们可以得到当前点（即第一次迭代结果）的最优解。继续按照这个迭代过程，我们可以逐步优化目标函数，并找到满足约束条件的最优解。

其中我们可以使用Scipy强大的库来实现！！（不解决这个问题，都没用过Scipy的库不知道其的强大！！）

#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Time    : 2023/8/31 21:41
# @Author  : AI_magician
# @File    : 原生python实现.py
# @Project : PyCharm
# @Version : 1.0,
# @Contact : 1928787583@qq.com",
# @License : (C)Copyright 2003-2023, AI_magician",
# @Function:


learning_rate = 0.00000001
num_iterations = 1000


# 定义目标函数
def objective(params, x, y):
    a, b, c, d = params
    # y_pred = a * x ** 3 + b * x ** 2 + c * x + d
    # residuals = y - y_pred
    return sum((y[i] - (a * x[i] ** 3 + b * x[i] ** 2 + c * x[i] + d)) ** 2 for i in range(len(x)))


# 定义目标函数的梯度
def gradient(params, x, y):
    a, b, c, d = params
    grad_a = -2 * (y - (a * x ** 3 + b * x ** 2 + c * x + d)) * x ** 3
    grad_b = -2 * (y - (a * x ** 3 + b * x ** 2 + c * x + d)) * x ** 2
    grad_c = -2 * (y - (a * x ** 3 + b * x ** 2 + c * x + d)) * x
    grad_d = -2 * (y - (a * x ** 3 + b * x ** 2 + c * x + d))
    return [grad_a, grad_b, grad_c, grad_d]


# 定义约束条件
def constraint(x, params):
    a, b, c, d = params
    derivative = 3 * a * x ** 2 + 2 * b * x + c  # x 的一阶导数恒大于0
    # print(derivative)
    return derivative


def adjust_gradient(gradient):
    adjusted_gradient = []
    # print(gradient)
    for grad in gradient:
        adjusted_gradient.append(max(grad, 0))
    return adjusted_gradient



# 定义 SLSQP 算法
def slsqp_algorithm(objective, gradient, constraint, x, y, initial_params, max_iter=100000):
    params = initial_params
    cons = (dict(type='ineq', fun=constraint))
    params = minimize(objective, x0=params, method='SLSQP', constraints=cons)
    if not res.success:
        print(res)
        raise ValueError('optimization failed')
    return res.x
    return params


# 初始化参数
initial_params = [1., 1., 1., 1.]  # 初始参数值

if __name__ == "__main__":
    import matplotlib.pyplot as plt
    import numpy as np

    # x_a = [19614.84, 12378.01, 5522.57, 3214.22, 1799.61, 894.12]
    # y_a = [44.85, 44.87, 43.75, 32.05, 27.37, 25.14]
    x_a = [5631.53, 3525.00, 1510.55, 868.94, 485.06, 242.01]
    y_a = [44.62, 44.24, 43.18, 41.39, 36.60, 28.84]
    x_a = np.log10(x_a)
    x_a = list(x_a)
    # 使用 SLSQP 算法求解非线性优化问题

    coef_a = slsqp_algorithm(objective, gradient, constraint, x_a, y_a, initial_params)

    # 打印结果
    print("优化结果:")
    print("a =", coef_a[0])
    print("b =", coef_a[1])
    print("c =", coef_a[2])
    print("D =", coef_a[3])

    print("-----------for trinomials function --------------------")

    print(f"coefficients: {coef_a}")

    print(f"total error for six points is : {objective(x=x_a, y=y_a, params=coef_a)}")

    print(f"constraint: {constraint(x=x_a[0], params=coef_a)}")

    p = np.poly1d(coef_a)

    # # 创建x轴上的一系列点，用于绘图
    x_plot = np.linspace(min(x_a), max(x_a), 400)

    # # 使用拟合的多项式计算这些点的y值
    y_plot = p(x_plot)

    # # 绘图
    plt.figure(figsize=(10, 6))
    # plt.scatter(x_a, y_a, color='red', label='Data points')
    plt.scatter(x_a, y_a, color='blue', label='Data points')

    plt.plot(x_plot, y_plot, label='polynomial fit')
    plt.xlabel('X')
    plt.ylabel('Y')
    plt.legend()
    plt.show()

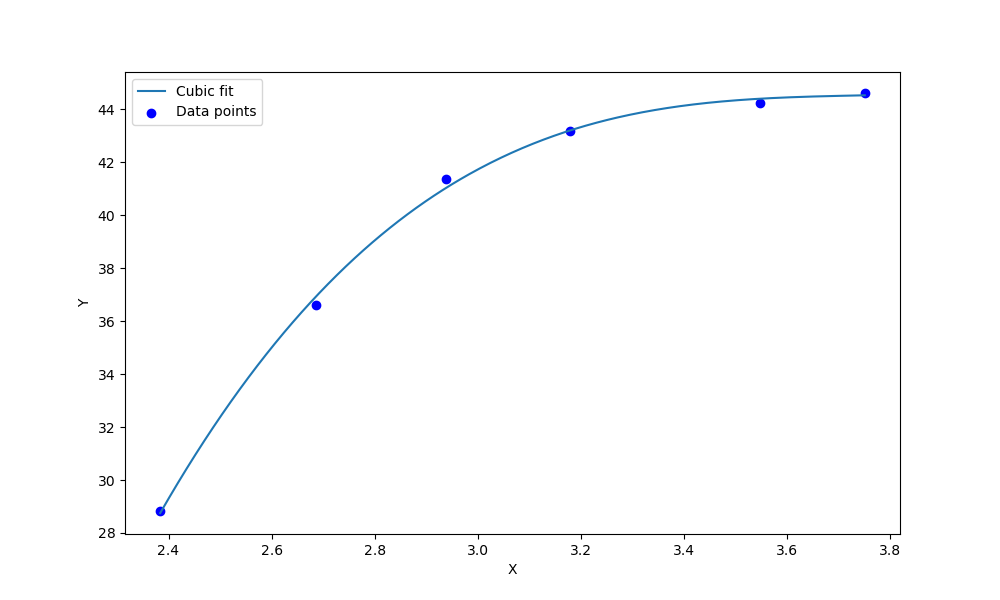
误差只有0.27 ！！！ 效果极佳！！

总结

总的来说，我们来看一下这两种算法的比较：

梯度下降算法是一种迭代优化方法，通过计算目标函数的梯度方向来更新参数。它适用于连续可导的目标函数，并且可以在大规模数据集上进行有效计算。然而，梯度下降算法可能会受到局部最小值、学习率选择以及收敛速度等问题的影响。

相比之下，SLSQP（Sequential Least Squares Programming）算法是一种约束优化方法，适用于存在约束条件的问题。它使用序列二次规划来求解问题，并且能够处理线性和非线性约束。SLSQP 算法通常需要更多计算资源和时间来找到全局最优解。SLSQP算法在面对少量数据时可能比梯度下降算法效果好的原因有以下几点：

1. 高精度：SLSQP算法是一种数值精确的优化方法，它使用序列二次规划来求解问题。相比之下，梯度下降算法是一种迭代方法，其收敛速度和最终结果受到学习率等参数选择的影响。在处理少量数据时，SLSQP可以更准确地找到全局最优解。

2. 约束处理：SLSQP算法适用于存在约束条件的问题，并且能够有效地处理线性和非线性约束。这使得它在需要考虑多个限制条件或复杂问题时更具优势。

3. 全局最优解：由于SLSQP采用序列二次规划方法，在搜索过程中会进行多次迭代以寻找全局最优解。而梯度下降通常只能保证找到局部最优解，特别是当目标函数非凸或存在平坦区域时。因此，在面对少量数据并且希望获得全局最佳结果时，SLSQP可能会表现更好。

因此，在选择使用哪个方法时需要考虑具体情况。如果你在无约束环境中工作并且有大量数据，则梯度下降可能更合适。而对于带有约束条件或非线性问题，则可以尝试使用 SLSQP 算法。为了确定最佳方法，请根据实际需求进行实验比较，并根据结果选择最适合的算法。

还有就是好好学数学！！数理统计与概率论以及离散数学等 优化算法等等数学理论知识，要想走算法这很重要！！

						  🤞到这里，如果还有什么疑问🤞
					🎩欢迎私信博主问题哦，博主会尽自己能力为你解答疑惑的！🎩
					 	 🥳如果对你有帮助，你的赞是对博主最大的支持！！🥳