5 小分子应用的AI
在化学中,小分子指的是相对分子量较低的有机化合物。它通常由少量原子组成,通常少于100个,并具有明确定义的化学结构。小分子与大分子相对比,大分子如蛋白质、核酸和聚合物在大小上要大得多,通常具有复杂的结构。在小分子学习中使用AI方法可以开发更准确和高效的分子预测和生成任务方法。在本节中,我们考虑了分子学习中的几个关键任务,包括分子表示学习、分子构象生成、从头生成分子、分子动力学模拟以及立体异构体和构象灵活性的表示学习,如图17所总结的。

图17. 小分子AI中的任务和方法概述。在本节中,我们考虑了五个任务,包括分子表示学习、分子构象生成、从头生成分子、分子动力学模拟以及学习立体化学和构象灵活性。在分子表示学习中,l = 0的情况对应于不变的方法,包括SchNet [Schütt等人2018],DimeNet [Gasteiger等人2020],SphereNet [Liu等人2022f],GemNet [Gasteiger等人2021]和ComENet [Wang等人2022g]。l = 1的情况对应于具有一阶向量特征 𝒗 ∈ R𝑑×3 的等变方法,包括EGNN [Satorras等人2021a],GVP-GNN [Jing等人2021],PaiNN [Schütt等人2021],ClofNet [Du等人2022],Vector Neurons [Deng等人2021]和EQGAT [Le等人2022]。l ≥ 1的情况对应于具有阶数l特征 𝒉l ∈ R𝑑×(2l+1) 的等变方法,包括TFN [Thomas等人2018],Cormorant [Anderson等人2019],𝑆𝐸(3)-Transformer [Fuchs等人2020],NequIP [Batzner等人2022],SEGNN [Brandstetter等人2022a],Equiformer [Liao和Smidt 2023]和MACE [Batatia等人2022b]。在分子构象生成中,一类方法的目标是学习低能量几何形状的分布,包括CVGAE [Mansimov等人2019],GraphDG [Simm和Hernández-Lobato 2019],ConfVAE [Xu等人2021d],CGCF [Xu等人2021a],ConfGf [Shi等人2021],GeoDiff [Xu等人2022b]和Torsional Diffusion [Jing等人2022]。另一类方法的目标仅是预测平衡基态几何形状,包括GeoMol [Ganea等人2021],EMPNN [Xu等人2023c]和DeeperGCN- DAGNN+Dist [Xu等人2021b]。在从头生成分子中,一类方法的目标是直接生成3D分子的坐标矩阵,包括E-NFs [Satorras等人2021b],EDM [Hoogeboom等人2022]和GeoLDM [Xu等人2023a]。另一类方法是通过 𝑆𝐸(3)-不变特征隐式生成3D原子位置,包括EDMNet [Hoffmann和Noé 2019],G-SchNet [Gebauer等人2019]和G-SphereNet [Luo和Ji 2022]。在分子动力学模拟中,简要介绍了包括ML力场 [Unke等人2021c],增强取样 [Sidky等人2020a]和粗粒化方法 [Noid 2023]在内的研究方向。学习立体化学侧重于通过采用启发式特征(Chemprop [Yang等人2019],MolKGNN [Liu等人2022g])或设计手性消息传递操作(Tetra-DMPNN [Pattanaik等人2020],ChIRo[Adams等人2021])来编码四面体手性。表示构象灵活性涉及学习构象不变性[Adams等人2021]或明确编码多实例构象集合[Axelrod和Gomez-Bombarelli 2020; Chuang和Keiser 2020]。
5.1 概述
作者:刘蒙,季水旺
由于2D分子图的机器学习方法已经得到广泛探讨并取得了令人鼓舞的结果[ Gilmer等人2017;Wu等人2018;Yang等人2019;Hu等人2020;Wang等人2022h,e;Edwards等人2022;Veličković2023],因此在这里,我们着重研究了对3D几何分子进行建模,这是一个更具挑战性和实际意义的角度。分子的3D几何形状在许多分子预测和生成任务中起着至关重要的作用。具体而言,分子的3D几何形状在确定许多重要性质方面起着关键作用,例如量子性质[ Ramakrishnan等人2014;Schütt等人2018;Liu等人2022f,2021a,2023a]以及其与靶蛋白的结合亲和力,这在很大程度上取决于分子和靶蛋白的互补3D形状[ Anderson 2003]。因此,使用预测和生成的AI方法对3D分子几何进行建模具有巨大潜力。特别是,它可以显著提高预测分子性质的准确性,并生成具有所需性质的新分子。
在分子表示学习中,考虑到3D分子几何,我们的目标是学习各种下游任务的信息表示,如分子级预测和原子级预测。期望这些表示能够捕获分子的准确结构和化学特性。这个任务是基础的,因为它是许多高级主题的基础,如药物发现、材料设计和化学反应。本节中我们考虑的下两个任务是生成任务。具体来说,分子构象生成是一个有条件的生成任务,我们的目标是生成给定2D分子图的低能量几何形状或平衡基态几何形状。这可以为获得3D分子几何形状提供了一种替代计算密集型方法,如密度泛函理论,因此在加速分子模拟应用中具有重要潜力。此外,在某些应用中,所需的2D分子图是未知的,我们有兴趣从头生成所需的3D分子。因此,在从头生成分子的任务中,我们的目标是用生成方法对3D分子几何空间的分布进行建模。这可以作为生成具有所需性质的新分子的第一步,用于药物发现、材料科学和其他应用。除了通用的分子表示学习,学习模拟分子动力学特别重要,这使我们能够捕获分子系统的时间相关行为,提供对其物理性质和结构变换的宝贵见解。AI方法主要通过提高力场的准确性、增强取样方法和实现有效的粗粒化来促进分子动力学模拟领域的发展。最后,我们考虑分子结构的固有复杂性,以实现更有效的表示学习。具体来说,我们讨论了分子立体化学和构象灵活性在分子表示学习中的重要性。
由于我们在三维空间中建模分子,因此有必要考虑底层的等变性和不变性特性。在3D分子学习任务中保持所需的对称性对于获得准确的预测和确保系统的物理约束至关重要。此外,如何准确捕获3D信息,如区分相同分子的对映异构体,是实现有效建模的另一个重要考虑因素。
5.2 分子表示学习
作者:Limei Wang,Zhao Xu,Montgomery Bohde,Chaitanya K. Joshi,Haiyang Yu,Meng Liu,Simon V. Mathis,Alexandra Saxton,Yi Liu,Pietro Liò,Shuiwang Ji
建议先修知识:第2.3节,第2.4节
在本节中,我们研究了分子表示学习的问题,旨在学习给定输入分子的信息表示。学到的表示可以用于各种下游任务,如分子级别预测和原子级别预测。此外,本节介绍的表示学习模型可以看作是启用更高级应用的骨干,如药物发现和材料设计的基础。
5.2.1 问题设置
分子图和点云:分子可以表示为2D分子图,其中包含图的拓扑结构(原子之间的化学键)以及节点和边缘特征,或者表示为3D分子图,其中还考虑了每个节点的3D坐标。虽然2D表示足以描述分子的化学特性,但分子的3D构型(称为构象)对于确定分子的许多实验相关性质(如能量或电偶极矩)是相关的。因此,我们将在本节的其余部分中重点介绍处理3D分子图的方法。形式上,我们将3D分子表示为包含 𝑛 个原子的点云 𝑀=(𝒛,𝐶),其中 𝒛=[𝑧,...,𝑧 ]∈Z𝑛 是原子类型的1𝑛向量,𝐶 = [𝒄1, ..., 𝒄𝑛] ∈ R3×𝑛 是原子坐标矩阵。为了从这个点云中获得分子图,可以添加边缘,例如从化学键(2D图的拓扑结构),从径向距离截断或从 𝑘 个最近邻居。由于边的构造因方法而异(下面进一步讨论),我们将一个分子称为其点云 𝑀 = (𝒛,𝐶)。
任务设置:我们的目标是学习3D分子的潜在表示,可用于下游预测任务和应用。有两种类型的下游预测任务:分子级别的预测和原子级别的预测。对于分子级别的属性预测任务,我们旨在学习一个函数 𝑓 (M) 来预测任何给定分子 M 的属性 𝑦。在这里,𝑦 可以是一个实数(回归问题,如构象的能量),一个整数(分类问题,如毒性),或一个张量(如电偶极矢量或惯性张量)。如果目标属性 𝑦 是标量/张量数量,它需要对参考框架的变化保持不变/等变。对于原子级别的属性预测任务,我们旨在学习一个函数 𝑓 来预测第 𝑖 个原子的属性 𝑦𝑖,例如用于分子模拟的每原子力。同样,𝑦 可以是标量或张量目标属性。
5.2.2 技术挑战
与典型的仅具有拓扑结构的2D图不同,3D结构的几何形状对3D分子建模提出了独特的挑战。
(1) 第一个挑战是,学到的表示应与物理几何量相对应,并应根据不同应用遵循基础对称性[Bogatskiy等人2022]。具体而言,对于像能量预测这样的任务,学到的表示应该是 𝑆𝐸(3)不变的。这意味着如果输入分子被旋转或平移,学到的表示应保持不变。对于像每原子力预测这样的任务,表示应该是 𝑆𝑂(3)等变的。这是因为如果输入分子被旋转,预测目标(例如力)应相应旋转。
(2) 另一个挑战是学到的表示的理论表达能力[Joshi等人2023],它体现为模型在区分分子的不同3D几何形状(如对映异构体和同一分子的不同构象)方面的实际限制。学到富有表现力的分子表示对于应用如药物设计和分子模拟[Pozdnyakov等人2020]至关重要。例如,手性药物的对映异构体可以与其他手性分子和蛋白质产生非常不同的相互作用。同一分子的不同构象也具有不同的电能和每原子力。
(3) 第三,效率是设计分子表示学习模型时需要考虑的重要因素。高效性能能够实现快速训练和推断,降低计算资源消耗,并增强对大规模真实数据集的可扩展性。
5.2.3 现有方法概述
如上所述,2D分子图包含了图的拓扑结构以及原始节点和边缘特征,基于这些特征,3D分子图进一步考虑了每个节点的三维坐标。从这些三维坐标可以计算出几何量,如距离、角度和扭角。更一般地说,如在第2节中介绍的那样,每个节点都具有一个顺序为l的SE(3)-等变节点特征。从张量阶的角度来看,现有的3D分子表示学习方法可以分为具有仅l = 0标量类型特征的不变3D图神经网络(3D GNNs)[Schütt等人2017a; Smith等人2017; Chmiela等人2017; Zhang等人2018a,b; Unke and Meuwly 2019; Schütt等人2018; Ying等人2021; Luo等人2023b; Gasteiger等人2020; Liu等人2022f; Gasteiger等人2021; Wang等人2022g]、具有l = 1矢量类型特征的等变3D GNNs [Schütt等人2021; Jing等人2021; Satorras等人2021a; Du等人2022, 2023a; Thölke and Fabritiis 2022] 和具有l ≥ 1张量特征的等变3D GNNs [Thomas等人2018; Fuchs等人2020; Liao and Smidt 2023; Batzner等人2022; Batatia等人2022a,b]。具体来说,不变方法直接将不变的几何特征,如距离和角度,作为输入,因此,无论输入分子如何旋转和平移,所有内部特征都保持不变。相比之下,等变方法中的内部特征应该根据输入分子的旋转或平移而相应变换。
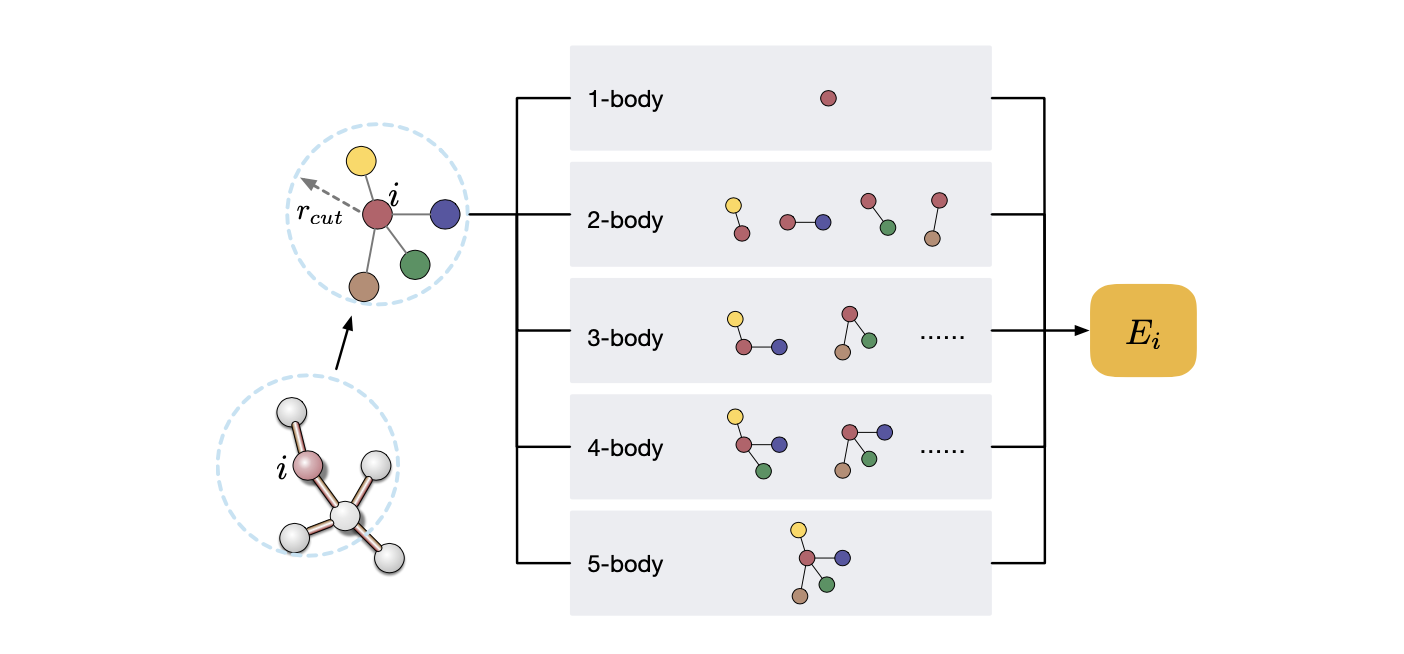
图18. 分子能量预测中的体序展开示例。首先,通过一个截断距离𝑟cut确定了中心原子𝑖的邻居节点和边。然后,𝑣体项考虑了中心原子𝑖和其1-hop邻居中的𝑣−1个所有组合。最后,原子𝑖的局部能量被计算为所有体序函数的线性组合。与体序展开方法[布朗等人2004; Braams和Bowman 2009]相比,标准的消息传递方法[Gilmer等人2017]仅考虑了体序为2,因为每个消息只涉及中心原子和一个邻居原子。
除了张量阶,从体序的角度看,现有的3D GNN层还可以进一步分类。体序来源于将势能面(PES)分解为体序函数的线性组合。传统方法[布朗等人2004; Braams and Bowman 2009]表明,如图18所示的体序展开在近似分子和材料系统的PES时具有高精度和快速收敛性。作为总分子能量的组成部分,我们可以将原子的局部能量写成体序展开的形式。
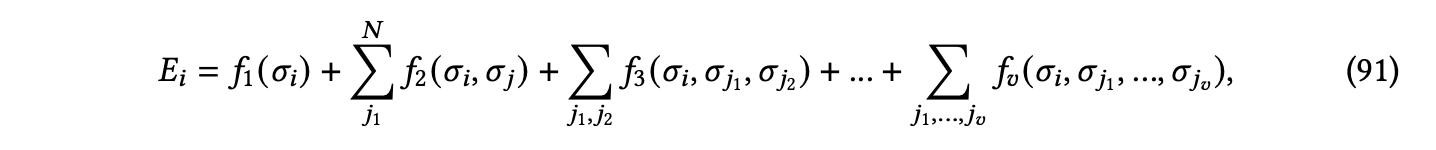
其中,𝑖是中心原子的索引,𝑗𝑘是𝑖的一个邻居节点的索引,𝑁是原子𝑖的总1-hop邻居数,𝜎表示原子状态,包括对应下标原子的原子属性和坐标。通常,在体序展开中,𝑣体项考虑中心原子和其1-hop邻居中的𝑣−1个的所有组合。因此,标准的消息传递[Gilmer等人2017]...
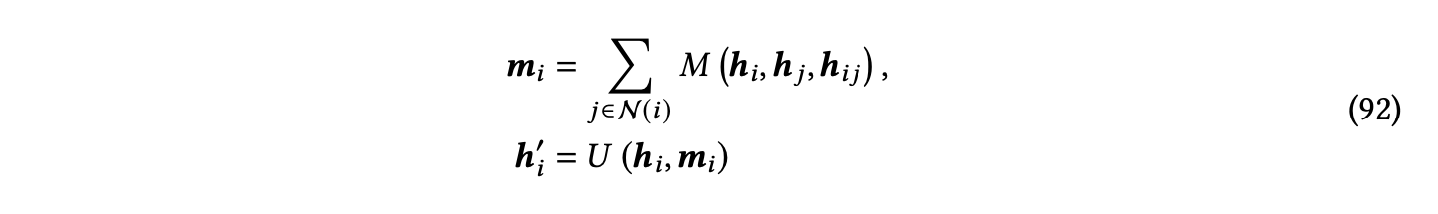
其中,N(𝑖)是节点𝑖的邻居节点集合,ℎ𝑖𝑗是节点𝑖和节点𝑗之间的边特征,例如边长度和边类型,𝑈和𝑀是更新和消息函数。尽管标准消息传递可以通过迭代层进一步聚合沿边的许多节点的信息,但这种聚合与局限在中心节点的1-hop范围内的多体相互作用不同。在本小节中,我们根据它们的张量阶和体序来讨论现有的基于3D分子表示学习的方法,如图19所总结。
5.2.4 不变方法(l = 0标量特征)
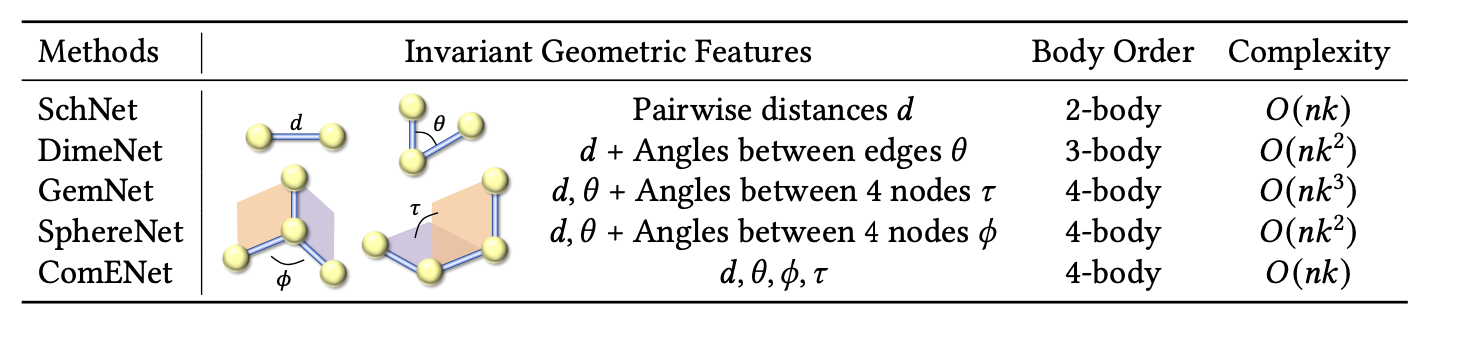
不变方法仅保持不变的节点、边或图特征,如果输入的3D分子被旋转或平移,这些特征不会改变。不变方法面临着在考虑多体几何特征以提高它们的区分能力和保持它们的效率之间的权衡,如表5所总结的。让𝑛和𝑘表示分子中的节点数和平均度。具体来说,SchNet [Schütt等人2018]仅在节点中心的消息传递模式中考虑成对距离作为边特征ℎ𝑖𝑗,导致复杂度为𝑂(𝑛𝑘),体序为2。DimeNet [Gasteiger等人2020]进一步考虑了边缘消息传递中每对边之间的角度。
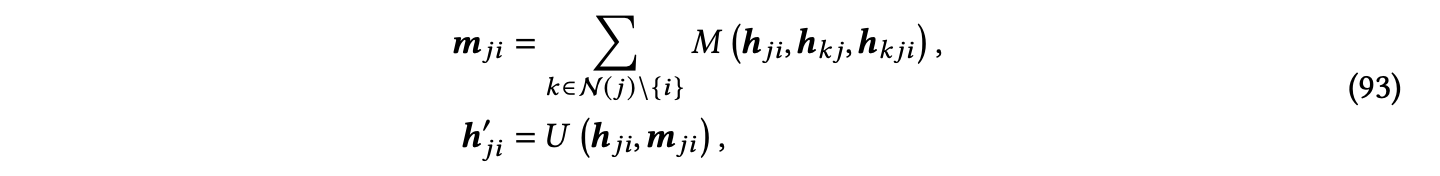
而且,复杂度是O(𝑛𝑘^2)。这里N(𝑗)\{𝑖}是节点𝑗的邻居节点集合,除了节点𝑖,𝒉𝑘𝑗𝑖是节点𝑘,𝑗和𝑖的特征,比如角度𝜃𝑘𝑗𝑖,𝑈和𝑀是更新和消息函数。GemNet [Gasteiger等人2021]进一步考虑了两跳二面角,将体序增加到4,复杂度增加到O(𝑛𝑘^3)。SphereNet [Liu等人2022f]计算了两个平面之间的局部4体角度。为了减少复杂性,SphereNet不包括所有可能的角度,而是通过选择参考节点构建参考平面来减少角度的数量,同时保持O(𝑛𝑘^2)的复杂性。ComENet [Wang等人2022g]定义了完整的几何特征,可以区分所有不同的3D分子。具体来说,距离和角度𝑑,𝜃,𝜙是2体,3体和4体几何特征,并且可以用于识别局部结构。这里的局部结构指的是中心节点及其1-hop邻域。这是因为𝑑𝑖 𝑗,𝜃𝑖 𝑗,𝜙𝑖 𝑗可以确定节点𝑗在以𝑖为中心的局部球面坐标系中的相对位置。此外,旋转角𝜏还捕获了局部结构之间的剩余自由度。因此,ComENet能够为每个3D分子生成唯一的表示,能够区分自然界中所有不同的3D分子。此外,它遵循方程(92)中的以节点为中心的消息传递模式,通过选择1-hop邻域内的参考节点,复杂性仅为O(𝑛𝑘)。
除了将等变的3D信息转化为不变的特征(如距离和角度)的方法[Schütt等人2018; Gasteiger等人2020; Liu等人2022f; Gasteiger等人2021; Wang等人2022g],Du等人[2022, 2023a]提出了标量化来获得不变的特征。具体来说,标量化将等变特征转化为基于等变局部框架的不变特征。例如,给定一个等变框架(𝒆1, 𝒆2, 𝒆3),我们可以将一个3D向量𝒓𝑖𝑗 = 𝒄𝑖 − 𝒄𝑗转化为(𝒓𝑖𝑗 · 𝒆1,𝒓𝑖𝑗 · 𝒆2,𝒓𝑖𝑗 · 𝒆3)。这里𝒆1,𝒆2,𝒆3构成正交基。除了标量化,Du等人[2022, 2023a]还使用张量化将不变特征转化为等变特征。因此,这些方法可以保持不变和等变的内部特征,并需要同时进行不变操作和等变操作(参见第5.2.5和5.2.6节)来更新内部特征。

图19. 现有分子表示学习方法概览。我们根据特征的张量阶和GNN层的体序,对现有方法进行了分类,这是构建最强大的3D GNNs的两个关键设计选择,如Joshi等人[2023]和第5.2.10节中所讨论的。l = 0标量特征的不变方法在第5.2.4节中详细描述,l = 1矢量特征的等变方法在第5.2.5节中描述,l ≥ 1张量特征的等变方法在第5.2.6节中描述,以及更高体序方法在第5.2.7节中描述。此外,不同阶数的特征需要特定的操作来保持𝑆𝐸(3)等变性。在这里,我们列举了不同张量阶的方法所需的几个示例操作。具体而言,对于线性层,输入和输出特征之间的每条灰色线包含可学习的权重。偏置项只能添加到l = 0标量特征中,因为它会破坏l ≥ 1特征的等变性。此外,张量积,如2.4中介绍并在图6中说明,对于具有l ≥ 1张量特征的等变方法是另一个关键操作,因为它可以保持更高阶特征的𝑆𝐸(3)-等变性。本图经过许可改编自Joshi等人[2023]。
表5. 现有的用于分子表示学习的不变的3D图神经网络(l = 0)概述,包括SchNet [Schütt等人2018]、DimeNet [Gasteiger等人2020]、GemNet [Gasteiger等人2021]、SphereNet [Liu等人2022f]和ComENet [Wang等人2022g]。这里𝑛和𝑘表示分子中的节点数和平均度。复杂性取决于几何特征的计算和消息传递模式。
5.2.5 等变方法(l = 1 矢量特征)。
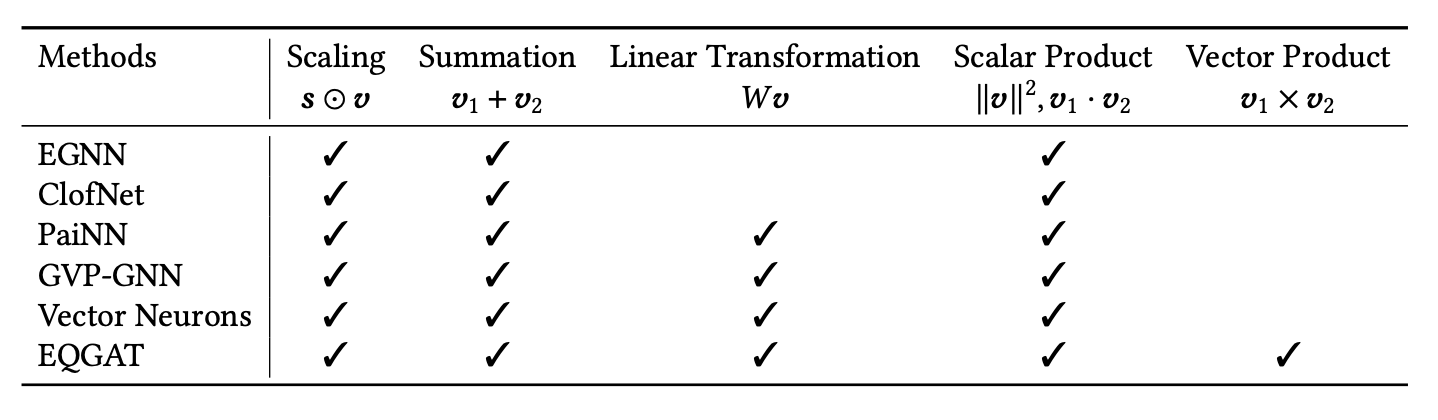
等变的3D GNNs的第一类别[Satorras等人2021a; Du等人2022; Schütt等人2021; Deng等人2021; Jing等人2021; Thölke和Fabritiis 2022]使用阶数为1的矢量作为中间特征,并通过一组受限制的操作来传播消息,以保证𝐸(3)或𝑆𝐸(3)的等变性,如表6所总结的。我们用𝒔∈R𝑑表示标量特征,用𝒗∈R𝑑×3表示矢量。如Schütt等人[2021]和Deng等人[2021]所总结的,可以确保等变性的矢量𝒗的操作包括矢量的缩放𝒔 ⊙ 𝒗,矢量的求和𝒗1 + 𝒗2,矢量的线性变换𝑊𝒗,标量积∥𝒗∥2,𝑣1·𝑣2,和矢量积𝑣1×𝑣2。这里⊙表示逐元素乘法。注意,𝑣1·𝑣2 = ∥𝑣1∥∥𝑣2∥cos𝜃和𝑣1×𝑣2 = ∥𝑣1∥∥𝑣2∥sin𝜃𝑛®,因此,使用标量积和矢量积可以隐含地包括角度和方向信息。
现有方法使用这些操作来通过传播标量和矢量消息来更新标量和矢量特征。例如,EGNN [Satorras等人2021a]使用矢量的缩放和矢量求和来确保等变性。具体来说,根据方程(92)的符号,EGNN层更新节点表示𝒉𝑖和节点坐标𝒄𝑖如下:
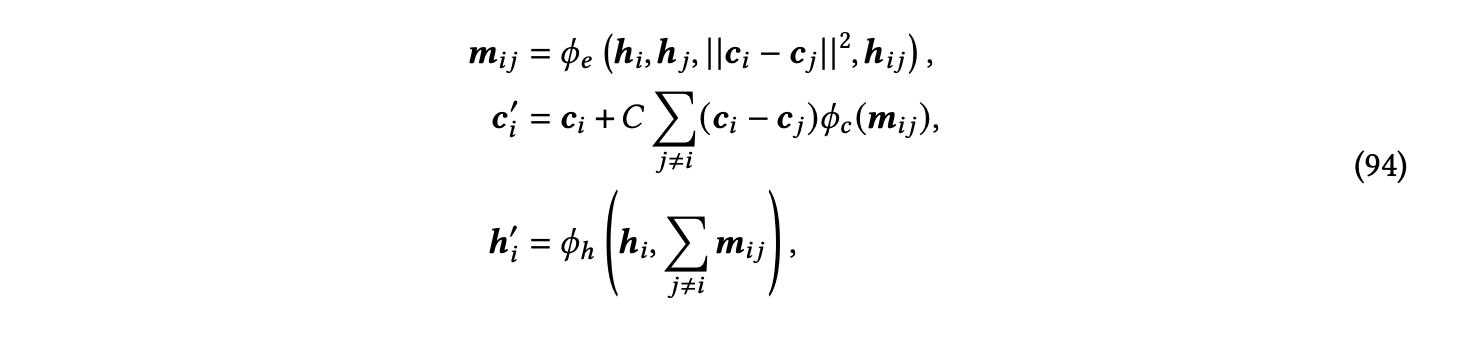
其中,𝜙𝑒,𝜙𝑐和𝜙h表示可学习的函数,𝐶是一个归一化因子。与只考虑每个边的单一矢量的EGNN不同,ClofNet [Du等人2022]使用了由三个矢量组成的完整框架来表示每个边。PaiNN [Schütt等人2021]在网络中进一步包括线性变换和标量积。GVP-GNN [Jing等人2021]使用与PaiNN类似的操作,最初是为了学习蛋白质结构的表示,但也可以适用于分子。矢量神经元 [Deng等人2021] 最初是为点云数据设计的,可以应用于分子。它还采用线性变换来实现阶数1矢量的线性算子。除了线性算子,矢量神经元还包括精心设计的非线性、池化和归一化层,这些层专为阶数1矢量而设计,同时确保所需的等变性。值得注意的是,它使用了可学习的方向,具有等变性,将域分成两个半空间,然后可以定义非线性层,如ReLU,来将这两个空间映射为不同的方式。除了上述操作,EQGAT [Le等人2022]在消息传递过程中使用叉积来更新等变特征。这使得类型1矢量特征之间能够进行交互,并允许更全面和富有表现力的特征表示。此外,它使用注意机制来捕捉节点之间的内容和空间信息。
表6. 使用l = 1矢量特征的等变方法的比较,包括EGNN [Satorras等人2021a]、ClofNet [Du等人2022]、PaiNN [Schütt等人2021]、GVP-GNN [Jing等人2021]、Vector Neurons [Deng等人2021]和EQGAT [Le等人2022]。这里𝒔∈R𝑑表示标量特征,𝒗∈R𝑑×3表示矢量特征。现有方法使用不同的操作来确保等变性。
5.2.6 等变方法(l ≥ 1 张量特征)。
另一类等变方法考虑了在第2节中讨论过的高阶(l ≥ 1)特征。在这个类别下,大多数现有方法使用更高阶球张量的张量积(TP)来构建等变表示,并遵循图20中的一般架构来更新特征,不同之处在于体序和技术细节。例如,TFN [Thomas等人2018]和NequIP [Batzner等人2022]遵循节点为中心的消息传递方案[Gilmer等人2017],根据邻近节点的消息来更新节点特征。由于每个消息包含中心原子和一个邻居的信息,这些方法自然具有体序为2。𝑆𝐸(3)-Transformer [Fuchs等人2020]和Equiformer [Liao和Smidt 2023]进一步增强了它们的模型架构,加入了注意机制。此外,Cormorant [Anderson等人2019]和SEGNNs [Brandstetter等人2022a]引入了不同设计的高阶特征的非线性。
一般来说,高阶等变模型为每个旋转阶数l ≤ lmax构建多个特征向量或“通道”。每个阶数l的通道长度为2l + 1。因此,节点𝑖的特征可以由𝒉l索引,其中l是旋转阶数,c是通道索引,m是每个通道的表示索引为(−l ≤ 𝑚 ≤ l)。高阶等变模型的一般架构如图20所示,我们将在下面描述每个组件。
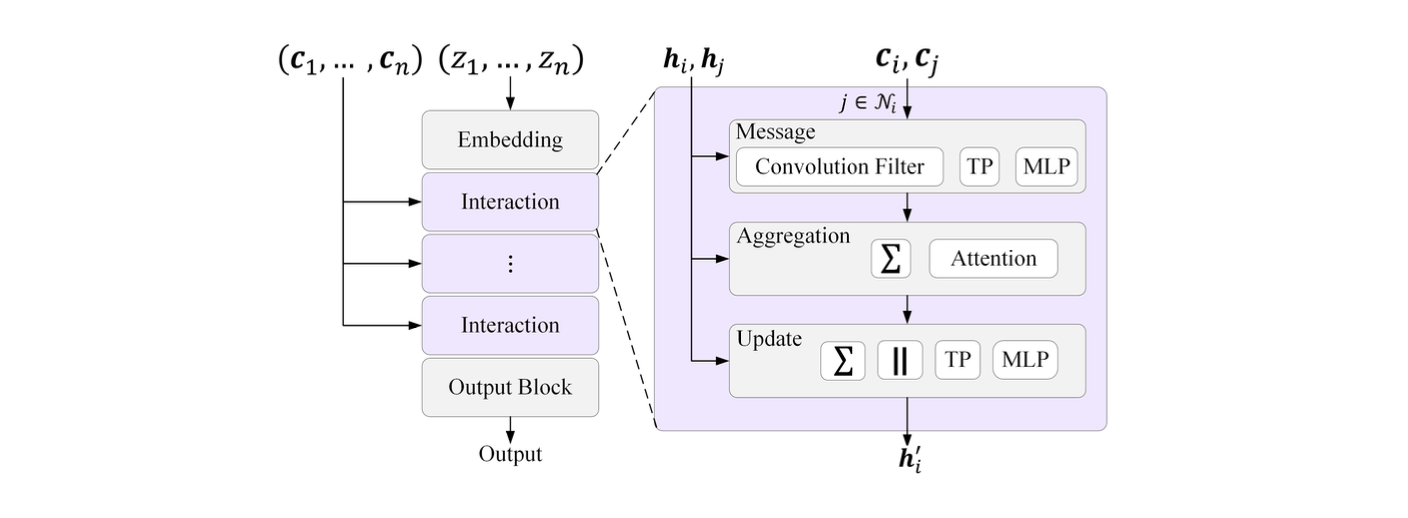
图20. 高阶等变模型的一般架构。每个模型由多个交互块组成,用于在原子之间执行成对的消息传递。这里,Σ表示求和,∥表示特征串联,TP表示特征向量的张量积,MLP表示多层感知器。每个消息、聚合和更新块中使用的具体操作在模型之间有所不同,但现有方法,如TFN [Thomas等人2018]、NequIP [Batzner等人2022]、𝑆𝐸(3)-Transformer [Fuchs等人2020]、Equiformer [Liao和Smidt 2023]、Cormorant [Anderson等人2019]和SEGNNs [Brandstetter等人2022a]都属于这一框架。
非线性函数:为了保持等变性,这些模型中使用的非线性函数受限于那些在表示索引𝑚中作为标量变换的函数。各种模型中使用的非线性函数如表7所示。值得注意的是,Cormorant只使用张量积作为唯一的非线性操作,𝑆𝐸(3)-Transformer使用注意力而不是其他模型中的非线性激活函数。
表7. 在高阶等变模型中使用的非线性函数。𝜂:R→R是一个非线性函数,例如SiLU或tanh,∥𝒉𝑐∥=𝑚|𝒉𝑐𝑚|,𝑏𝑐是可学习的偏置。
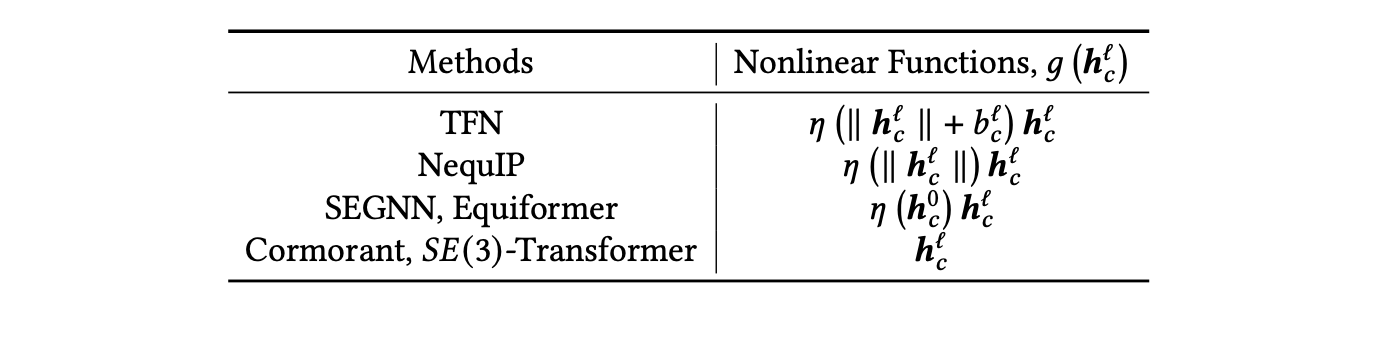
线性层:这些模型中使用的线性层的形式如下:
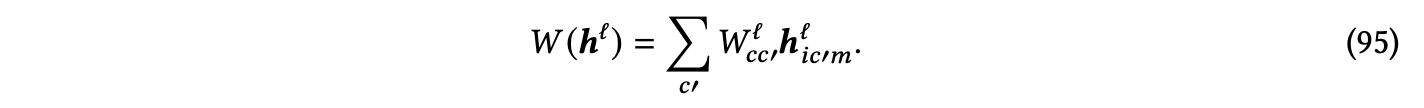
这些模型中使用的权重在𝑚维度上是恒定的,这是为了保持等变性。可选择地,可以为𝑙 = 0 特征添加偏置。
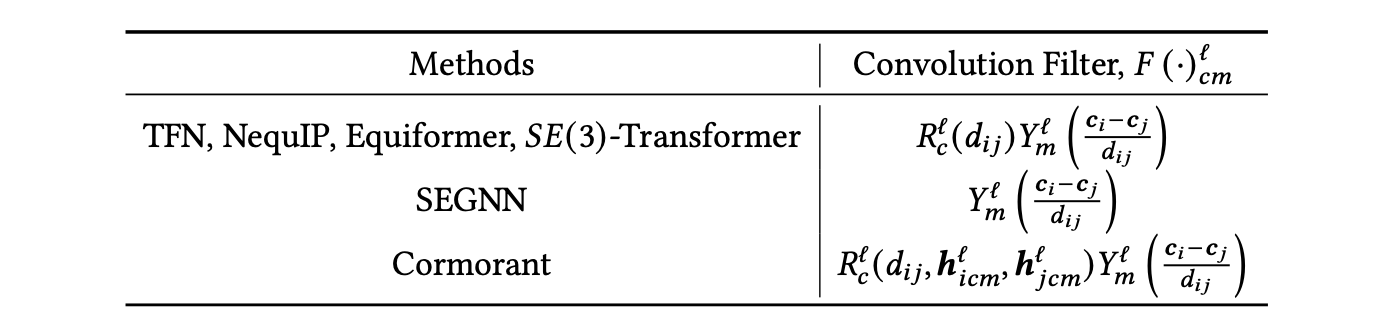
卷积滤波器:这些模型通常将卷积滤波器构建为可学习的径向函数和球谐函数的乘积。几个模型使用的具体滤波器如表8所示。
表8. 高阶等变模型中使用的卷积滤波器。这里,𝑑𝑖 𝑗是节点之间的距离。
消息:然后使用张量积构建成对的消息。所有方法都从卷积滤波器和节点特征的张量积开始,但一些方法进一步增强了这些消息。每个模型中用于计算消息的具体方程如表9所示。通常,阶数l1和l2的特征向量的张量积会产生所有旋转阶数的输出,满足|l1 − l2| ≤ l3 ≤ l1 + l2。第2.4节更详细地描述了张量积操作。
表9. 高阶等变模型中用于计算消息的方程。𝜙(·) = 𝑔(𝑊(·))。∥表示特征的串联。出于简洁起见,省略了l、𝑐和𝑚的消息索引。

聚合:对于每个原子,然后在相邻原子之间聚合消息。对于所有模型,都使用了求和聚合,然而,𝑆𝐸(3)-Transformer和Equiformer首先使用注意力来加权传入的消息。每个模型使用的聚合函数如表10所示。注意,𝑆𝐸(3)-Transformer使用点积注意力。Equiformer使用更强大的MLP注意力,但为了保持等变性,只使用l = 0特征来计算注意力分数。
表10. 高阶等变模型中使用的聚合函数。𝛼𝑖 𝑗 是注意力分数。

更新:最后,聚合的消息用于更新每个节点的特征。每个模型中使用的具体更新函数如表11所示。在TFN和𝑆𝐸(3)-Transformer中,层之间没有使用残差连接。然而,后续的研究表明,为了保留化学信息,如原子类型,这种连接至关重要。
5.2.7 高体序方法。
以前的等变图网络层使用了来自邻居到中心节点的方向向量的球谐函数来考虑二体相互作用。高体序方法包括
表11. 高阶等变模型中使用的更新函数。

邻居之间的多体相互作用。为了更好地逼近原子势能,引入了多体分解[Drautz 2019],如下所示:
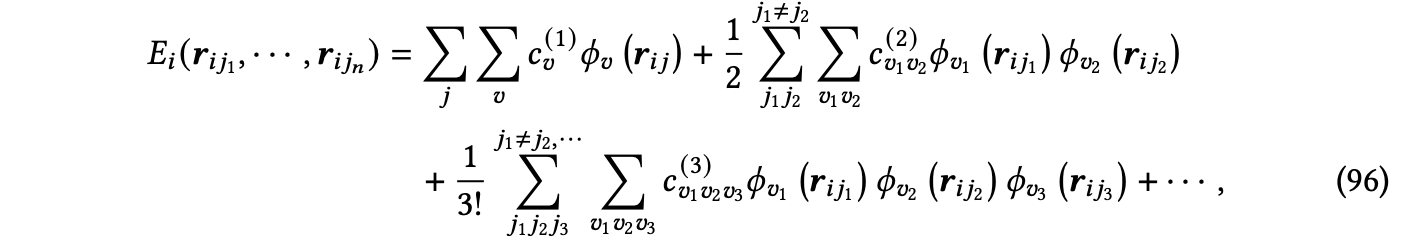
其中,𝜙𝑣是单键基函数,𝒓𝑖𝑗表示从节点𝑖到𝑗的方向向量,𝑐是系数。然而,多体分解的复杂性是𝑂(𝑛𝑑),这表明随着邻居数𝑛的增加,复杂性呈指数增加。这里,𝑑对应于体序。为了降低复杂性,原子簇展开(ACE)[Drautz 2019; Dusson等人 2022]使用原子基函数𝐴𝑖𝑣 = Í𝑗 𝜙𝑣 (𝒓𝑖 𝑗 )来表示原子能量,如下所示:
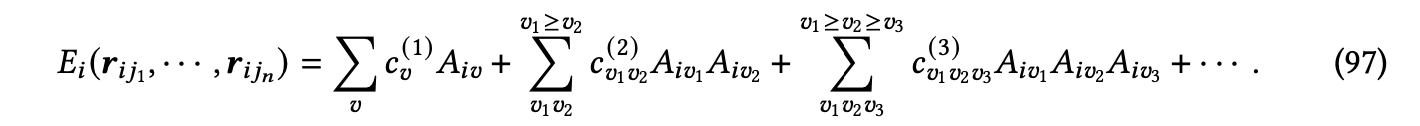
因此,可以保持与邻居数目的线性增长。在ACE之后,许多机器学习方法[Dusson等人 2022; Drautz 2019; Batatia等人 2022b,a; Musaelian等人 2023a; Kondor 2018; Li等人 2022h; Bigi等人 2023; Kovacs等人 2023; Musaelian等人 2023b; Batatia等人 2023]被开发出来以考虑更高体序的相互作用。
线性ACE和MACE是基于“密度技巧”理论开发的,线性ACE依次构建粒子基函数、原子基函数、积基函数、对称化基函数,最后使用对称化基函数的线性组合来高效构建高体序特征。线性ACE模型[Kovács等人 2021]只包含一个层,而MACE[Batatia等人 2022b,a]利用张量积并进一步扩展到多个ACE层,以扩大感受野,从而通过消息传递也包含了半局部信息。与使用ACE获取节点的聚合消息不同,Allegro[Musaelian等人 2023a]将操作集中在边缘上。具体而言,Allegro在中心节点周围的边缘之间执行张量积,并通过一系列层增加体相互作用的阶数。由Allegro产生的多体嵌入类似于ACE的对称化基函数,尽管不是严格等价的。除了上述方法外,Wigner核[Bigi等人 2023]开发了在具有较低成本的径向元素空间中计算的体序核,其成本与最大体序呈线性关系。N体网络[Kondor 2018; Li等人 2022h]是一个层次化神经网络,旨在基于多体系统的分解来学习原子能量。在现有的多体方法中,线性ACE、MACE和Allegro遵循图20总结的一般架构。
卷积滤波器:高体序方法中使用的卷积滤波器总结如表12所示。与第5.2.6节中的NequIP等方法类似,MACE将卷积滤波器构建为可学习的径向函数和球谐函数的乘积。线性ACE和Allegro没有卷积滤波器。
表12. 在高体序方法中使用的卷积滤波器。

消息:如表13所示,线性ACE将消息构建为径向基函数和球谐函数的乘积,其中径向基函数𝑅𝑙与节点𝑖和𝑗的原子类型相耦合。
𝑐,𝑧𝑖𝑧𝑗
MACE将消息构建为卷积滤波器和节点特征的线性变换的张量积。MACE使用的线性变换与第5.2.6节中的相同。
Allegro通过将来自前一层的不变特征𝒙𝑡−1传递给一个MLP,然后将输出与球谐函数相乘来构建消息。
表13. 高体序方法中用于计算消息的方程。

聚合:高体序方法中使用的聚合函数总结在表14中。在线性ACE和MACE中,聚合是按照原子簇展开(ACE)进行的。根据ACE,消息𝑚𝑖𝑗是用于表示原子𝑖和𝑗的2体粒子基函数。首先,将这些2体粒子基函数在相邻原子上求和,以获得中心原子𝑖的原子基函数。然后,原子基函数的乘积创建了一个𝑣+1体的乘积基函数。为了保持旋转等变性,将乘积基函数与广义克莱布斯-戈登系数相乘,以形成对称基函数。最后,每个原子的聚合多体消息是通过对不同体序的对称基函数特征进行线性组合来构建的。这里,l𝒎表示(l1𝑚1,...,l𝑣𝑚𝑣)的旋转次序路径,而附加的索引𝜂𝑣用于枚举导致所需输出旋转次序的所有旋转次序路径(l1,...,l𝑣)。在Allegro中,来自相邻边的消息在中心原子𝑖周围求和,以获得原子𝑖的聚合消息𝑚𝑖。
表14. 高体序方法中使用的聚合函数。

更新:高体序方法中使用的更新函数总结在表15中。线性ACE不需要更新节点特征,因为它只有一个单一层。MACE使用聚合消息和前一层的节点特征来更新每个节点的特征。在Allegro中,使用聚合消息𝑚𝑖来更新边𝑒𝑖𝑗的两个特征。第一个是通过聚合消息𝑚𝑖和前一层特征𝑣𝑖𝑗的张量积获得的等变特征𝑣𝑖𝑗。然后,提取𝑣𝑖𝑗的不变部分,以更新边𝑒𝑖𝑗的不变特征𝑥𝑖𝑗。
表15. 高体序方法中使用的更新函数。

输出:高体序方法的输出模块与其他等变方法不同。高体序方法首先为每个原子计算局部能量,然后分子的总能量是所有原子的局部能量之和。在线性ACE中,提取了聚合消息的不变部分作为每个原子的局部能量。在MACE中,原子的局部能量是一个固定项和一个可学习项的总和。固定项由原子类型确定,对应于该原子的孤立能量,这是使用DFT预先计算的。可学习项来自每层中获得的节点特征的不变部分。在Allegro中,最终层的不变边特征用于获取成对能量。接下来,围绕中心原子的成对能量与取决于原子类型的缩放因子𝜃𝑧𝑖𝑧𝑗 相乘。然后将它们求和以获得中心原子的局部能量。高体序方法中使用的输出函数总结在表16中。
表16. 高体序方法中使用的输出函数。

5.2.8 模型输出。
无论是不变的方法还是等变的方法,都应该能够处理不同任务和应用的对称性。不变方法可以直接生成 𝑆𝐸(3) 不变特征,某些等变特征也可以基于最终的不变特征来实现。例如,为了预测具有 𝑆𝑂(3) 等变性的每个原子的受力,不变方法首先预测能量 𝐸,然后使用能量对原子位置的梯度𝒇 = − 𝜕𝐸来计算每个原子的受力,从而确保能量守恒。这里 𝒄𝑖 是节点 𝑖 的坐标。等变方法也可以使用预测的能量来计算力或预测力。
对于其他等变预测目标,比如在第4节中讨论的哈密顿矩阵,不变模型需要额外的操作来确保等变性,这使得等变方法对于这些任务更加直接和适用。
表17。QM9 [Ramakrishnan et al. 2014]、MD17 [Chmiela et al. 2017]、rMD17 [Christensen and Von Lilienfeld 2020]、MD17@CCSD(T) [Chmiela et al. 2018]、ISO17 [Schütt et al. 2018] 和 Molecule3D [Xu et al. 2021b] 数据集的统计信息。我们总结了预测任务、3D 分子样本数量 (# 样本)、一个分子中的最大原子数 (最大 # 原子) 和一个分子中的平均原子数 (平均 # 原子)。

分子表示学习方法在各种任务上进行了评估,如能量预测和每个原子的力预测。表17总结了常用的数据集,包括QM9 [Ramakrishnan et al. 2014]、MD17 [Chmiela et al. 2017]、rMD17 [Christensen and Von Lilienfeld 2020]、MD17@CCSD(T) [Chmiela et al. 2018]、ISO17 [Schütt et al. 2018] 和 Molecule3D [Xu et al. 2021b]。通常,使用预测值和真实值之间的平均绝对误差和均方误差作为评估指标。
具体来说,QM9数据集[Ramakrishnan et al. 2014]收集了超过130,000个小有机分子,其中包括来自GDB-17数据库[Ruddigkeit et al. 2012]的最多九个重原子(CONF)。对于每个分子,该数据集提供了其稳定状态(能量最低)的3D几何结构,以及相应的谐波频率、偶极矩、极化率、能量、焓和解离能自由能。所有属性都是在量子化学的B3LYP/6-31G(2df,p)水平下计算的。通常,每个属性都会训练一个单独的模型。
MD17数据集[Chmiela et al. 2017]包括8个小有机分子的分子动力学模拟,分别是阿司匹林、苯、乙醇、马隆醛、萘、水杨酸、甲苯和尿嘧啶。对于每个分子,该数据集提供了数十万种构象和相应的能量和力。修订版MD17(rMD17)数据集[Christensen and Von Lilienfeld 2020]是MD17的重新计算版本,以减少数值噪音。对于原始MD17中的每个分子,取100,000个构型,并使用非常严格的自洽场收敛和非常密集的DFT积分格计算PBE/def2-SVP水平的理论下的能量和力。因此,该数据集几乎没有数值噪音。MD17@CCSD(T) [Chmiela et al. 2018]是基于更精确和昂贵的CCSD或CCSD(T)方法计算的,包含的分子较少。通常情况下,对于MD17、rMD17和MD17@CCSD(T),会为每个分子单独训练一个模型,任务是为每个构型预测能量和力。为了确保能量守恒,大多数方法从预测能量中计算出每个原子的力,如第5.2.8节所讨论的,通常使用的损失函数是能量损失和力损失的组合。
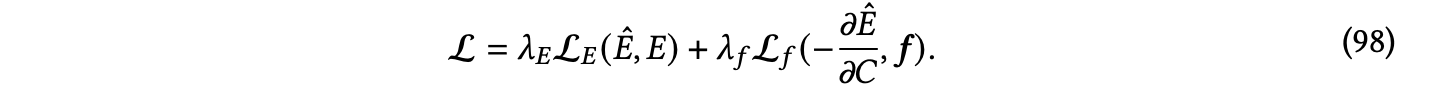
在这里,𝐸ˆ是预测的能量,−𝜕𝐸ˆ是计算得到的力,𝐶是原子坐标矩阵,𝐸和𝜕𝐶𝒇分别是真实的能量和力,L𝐸和L𝑓是能量和力损失函数,例如平均绝对误差和均方误差,𝜆𝐸和𝜆𝑓是能量和力损失的权重,通常设置为1和1000。
ISO17 [Schütt et al. 2018] 与MD17不同之处在于它包含了化学和构象上的变化。该数据集包含了129个同分异构体的分子动力学轨迹,这些同分异构体的组成都相同,均为C7O2H10。每个轨迹包含5,000个构象,总共有645,000个样本。与MD17不同,通常情况下,对于ISO17,一个常见的设置是在所有129种不同的分子上训练一个单一模型。
Molecule3D [Xu et al. 2021b] 是一个大规模数据集,包含约400万个从PubChemQC [Nakata and Shimazaki 2017]策划的分子。对于每个分子,该数据集提供了其精确的基态3D几何结构,该结构是从B3LYP/6-31G*水平的DFT中获得的,还提供了分子性质,如最高占据分子轨道(HOMO)和最低未占据分子轨道(LUMO)的能量,HOMO-LUMO间隙和总能量。虽然Molecule3D主要是为了从2D分子图预测3D几何结构而设计的(见第5.3节),但在本节中,我们可以直接将基态3D几何结构作为输入,并测试模型在性质预测任务上的性能。值得注意的是,PCQM4Mv2数据集 [Hu et al. 2020, 2021a] 也是从PubChemQC策划而来,但只提供了训练数据的3D几何结构。因此,它通常用于从2D分子预测性质[Ying et al. 2021]、预训练[Zaidi et al. 2023]和2D-3D联合训练[Luo et al. 2023b]等任务。
除了上述提到的数据集,本节讨论的一些分子表示学习方法还在较大的分子上进行了评估,例如蛋白质、材料、DNA和RNA。示例数据集包括MD22 [Chmiela et al. 2023]、Atom3D [Townshend et al. 2020] 和OC20 [Chanussot* et al. 2021]。
5.2.10 开放性研究方向。
从2D和3D信息中学习:尽管分子表示学习取得了一些进展,但仍然有一些需要进一步探索的挑战。一个方向是从分子的2D和3D信息中进行联合训练[Stärk et al. 2022a; Luo et al. 2023b]。虽然3D信息对于准确建模分子的物理性质至关重要,但计算成本高昂且难以从实验中获得。另一方面,2D信息,如分子图,计算效率高,但可能无法捕捉准确预测所需的所有信息。因此,探索可以在2D和3D信息上联合训练或从3D表示转移知识的方法可能会提高性能,同时在性质预测和药物发现等任务中提高效率。
表达力和计算效率:在理论方面,一个挑战是开发可以在完整或通用方式下捕捉原子之间几何相互作用的具有可证明表达力的3D GNNs[Pozdnyakov et al. 2020],如第2.9.3节所详述的。为了实现这一目标,Joshi等人[2023]在判别非同构几何图形方面提供了几何GNN表达能力的理论上限,并且一般来说,传播几何信息的等变层在表达能力上比不变层更具表现力。他们确定了构建最大功率等变GNNs的关键设计选择:(1)深度,(2)张量阶,(3)标量化体序。如本节所强调的,体序控制网络在节点附近的邻域内捕捉局部几何的能力,而更高的张量阶使网络能够在表示几何信息时具有更高的角分辨率。最后,网络深度控制了体系结构的感受域,在许多当前的等变体系结构中,增加深度隐含地也会导致增加体序。
尽管理论上增加这三个属性可以改进几何GNNs的表达能力,但一些实际挑战限制了具有可证明表达能力的模型。计算高阶张量[Passaro and Zitnick 2023]和多体相互作用[Batatia et al. 2022b]会显著增加计算成本,通常将实际使用的网络限制在张量阶𝑙 ≤ 2和体序𝜈 ≤ 4。此外,存在早期证据表明,随着深度的增加,几何过分压缩[Alon and Yahav 2021]。未来的研究可能集中在改进多体和高阶等变GNNs的效率,以适用于更大的生物分子以及更大的数据集。
不变与等变消息传递:不变GNNs比等变GNNs具有更高的可扩展性,并且在使用完全连接的图[ 2020 年Joshi]和预先计算非局部特征[ 2021 年Gasteiger等]时可以同样强大。同样,一些不变GNNs构建了规范参考框架,以将等变量转换为标量特征[Du等2022; Duval等2023],允许在网络中的所有中间表示上使用非线性。研究不变和等变消息传递之间的权衡是分子表示学习研究的另一个富有成果的领域。
5.3 分子构象生成
作者:Zhao Xu,Yuchao Lin,Minkai Xu,Stefano Ermon,Shuiwang Ji 推荐先修课程:第5.2节
正如第5.2节所讨论的,3D分子几何在分子表示学习中的作用至关重要,因为与仅使用2D图形相比,它们显着提高了性质预测的准确性。这种对3D信息的增强归因于分子的物理构型在很大程度上影响了其众多性质。例如,具有相同原子组成的同分异构体可能由于其分子结构的差异而具有完全不同的熔点。在免疫学中,抗体的结合位点的形状,特别是互补决定区(CDRs)的形状,精确地决定了它们可以识别和结合的抗原,这对于免疫反应至关重要。因此,在处理分子属性预测、分子动力学和分子-蛋白质对接等实际应用时,分子的空间信息是非常有价值的。然而,通过密度泛函理论(DFT)获得准确的3D几何结构是非常具有挑战性的,因为其高计算成本限制了广泛应用3D分子几何的范围。因此,利用机器学习模型来重建3D分子几何的方法已经成为一种有前途的替代方案,有望降低计算成本并使3D几何更易获得。
5.3.1 问题设置。
让分子中的原子总数为 𝑛。将2D分子表示为G = (𝒛, 𝐸),其中 𝒛 = [𝑧 ,...,𝑧 ] ∈ Z𝑛 表示原子类型向量,𝐸 中的每个 𝑒 ∈ Z 表示节点 𝑖 和 𝑗 之间的边类型。
1𝑛 𝑖𝑗
对于给定的2D分子G,相应的3D分子还需要3D几何结构 𝐶 = [𝒄1, ..., 𝒄𝑛] ∈ R3×𝑛,其中 𝒄𝑖 表示第 𝑖 个原子的3D坐标。 𝐶 的一种形式与势能相关联,从与Boltzmann分布相对应的势能表面中采样,该分布规定了在给定环境中更低势能状态更可能。
5.3.2 技术挑战.
从2D分子图中重建3D分子几何结构存在三个主要挑战。第一个挑战是确保获得的构象在3D空间中是几何有效的。例如,由于图神经网络(GNNs)固有的排列不变性,对称图节点可能具有相同的嵌入,从而导致无效的几何结构。因此,必须区分这些对称原子,并强制它们的重建坐标是不同的,因为原子在3D空间中不应重叠。此外,现有的研究[Simm和Hernández-Lobato 2019; Xu等,2021b]首先考虑了距离几何(DG),然后根据距离矩阵重建原子坐标。在这种情况下,由于导出的距离矩阵可能无法构成有效的欧几里德距离矩阵(EDM),确保原子坐标的3D几何有效性变得特别具有挑战性。除了保持重建构象的3D几何有效性之外,第二个挑战是满足构象片段施加的化学有效性。例如,芳香环或π键将所有其原子限制在一个平面上,而许多大环和小环是非平面的[Wang等,2020b]。希望重建的几何结构遵循这种量子规则,并且在化学上是有效的。在重建3D分子几何方面的另一个挑战来自几何密度函数的固有对称性。鉴于具有零质心(CoM)的初始系统[Xu等,2022b; Köhler等,2020],构象的生成几何分布通常被建模为不变分布,以便根据地面真实分布抽取渐近无偏的样本[Köhler等,2020]。具体而言,我们必须确保重建的构象受到𝑆𝐸(3)-不变位置分布的限制。给定旋转矩阵𝑅∈𝑆𝑂(3)⊂R3×3和平移向量𝒕∈R3以及1∈R𝑛,𝑆𝐸(3)-不变的位置分布要求𝑝(𝑅𝐶+𝒕1𝑇|𝐺)=𝑝(𝐶|𝐺)。换句话说,旋转或平移的构象被视为相同,因为几何重建与旋转和平移无关。
5.3.3 现有方法.
基于生成的方法:尽管存在大量的分子生成模型,但本节专注于那些对领域做出了最新和重要贡献的模型。许多早期的生成模型,如CVGAE [Mansimov等,2019],GraphDG [Simm和Hernández-Lobato 2019],Conf VAE [Xu等,2021d]和CGCF [Xu等,2021a],都是基于变分自动编码器(VAEs)或流模型作为它们的基本理论开发的。另一方面,当前的最新生成模型主要依赖于分数匹配和概率去噪扩散模型,具有𝐸(3)-等变/不变模块。例如,ConfGF [Shi等,2021]开发了一个3D生成模型,使用分数匹配来获得通过位置到距离的链式规则导数来计算的分数。为了生成分子中每个原子的位置,ConfGF在采样过程中应用𝐸(3)-等变模型来更新原子位置。GeoDiff [Xu等,2022b]通过合并零质心𝐸(3)-等变扩散概率模型,进一步扩展了ConfGF的功能。尽管这两种方法都可以直接生成分子的3D坐标,但它们没有考虑化学约束,例如芳香环中的所有原子都在同一个平面上。因此,它们可能会生成化学上无效的构象。相比之下,扭转扩散[Jing等,2022]仅使用𝑆𝐸(3)-不变扩散模型来调整构象的扭转,同时保留由RDKit生成的所有局部结构,如键长和角度。通过这样做,它利用了由RDKit引入的化学知识。然而,这种方法严重依赖于由RDKit生成的构象,并且不能调整局部环结构,如大环或小的非平面环。基于扭转扩散,DiffDock [Corso等,2022]将蛋白质-配体对接作为一种以蛋白质为条件的构象生成过程。我们将在第8节中详细描述DiffDock的细节。
表18. 总结了几种代表性的3D分子构象生成方法的3D输出、模型架构和分布对称性。在各种方法中,CVGAE [Mansimov等,2019]、GraphDG [Simm和Hernández-Lobato 2019]和ConfVAE [Xu等,2021d]使用条件变分自动编码器生成分子构象,其中CVGAE直接生成3D坐标,而GraphDG和ConfVAE生成分子构象的原子间距离。在ConfVAE的精神下,CGCF [Xu等,2021a]通过利用流生成模型来生成原子间距离。此外,ConfGf [Shi等,2021]和GeoDiff [Xu等,2022b]采用零质心的𝐸(3)-等变模型直接生成3D坐标,并实现了𝐸(3)-不变的生成分布。相反,Torsional Diffusion [Jing等,2022]应用了𝑆𝐸(3)-不变的扩散模型来专门生成扭转,保留了由RDKit生成的键长和角度等局部结构。此外,GeoMol [Ganea等,2021]、DeeperGCN-DAGNN+Distance [Xu等,2021b]和EMPNN [Xu等,2023c]实现了用于生成分子构象的预测策略。

预测为基础的方法:另一方面,其他现有的研究将任务制定为一个预测性任务,重点是预测平衡基态构象。一个例子是GeoMol [Ganea等,2021],它使用带有几何约束的消息传递神经网络(MPNNs)来预测局部结构以生成多样化的构象。为了确保几何有效性,GeoMol应用了一个匹配损失,通过在对称节点的所有可能排列中搜索与基本事实之间的最佳匹配子结构,有效地区分了对称原子。另一个值得注意的方法是[Xu等,2021b]中提出的DeeperGCN-DAGNN+Distance。这种方法旨在预测完整的距离矩阵,然后直接在下游任务中使用距离矩阵,因为成对距离隐含地提供了3D信息。相反,EMPNN [Xu等,2023c]使用节点索引来打破节点的对称性,并明确输出基态构象的几何有效的3D坐标。
为了全面概述领域内各种生成和预测方法,我们在表18中总结了代表性方法。
5.3.4 数据集和基准。
分子的几何构象集合(GEOM)[Axelrod和Gómez-Bombarelli 2022]是一个高质量的分子构象数据集,其中3D分子结构首先由RDKit [Landrum 2010]初始化,然后通过ORCA [Neese 2012]和CREST [Grimme 2019]程序进行优化。它包含两个子集,GEOM-QM9和GEOM-Drugs,是用于评估不同分子构象生成方法性能的常用基准数据集。GEOM-QM9数据集包含来自原始QM9数据集[Ramakrishnan等,2014]的133,258个小有机分子。该数据集中的所有分子都具有最多9个重原子和29个总原子,包括氢原子,分子质量很小,可旋转键很少。重原子的原子类型限制为碳、氮、氧和氟。相比之下,GEOM-Drugs包含较大的药物样分子,平均含有44.4个原子(24.9个重原子),最多含有181个原子(91个重原子)。最重要的是,这些大分子具有显著的灵活性,例如,平均含有6.5个旋转键,最多可达53个旋转键,这对于学习分子构象生成模型是具有挑战性的。
5.3.5 开放研究方向。
尽管在基于机器学习的分子构象生成模型中已经取得了重大进展,但未来研究仍有几个有前途的方向。首先,当前的基准数据集都是在真空环境中模拟的,而在现实中,分子的构象在周围的溶剂环境中是不同的。未来的研究可以集中于将溶剂效应纳入生成模型中,使其能够生成反映分子在给定溶剂环境中的实际行为的构象。其次,学习构象生成模型通常需要大量的训练数据。然而,在许多情况下,特定类别的分子或化合物只有有限的数据可用。未来的研究也可以探索迁移学习和少样本学习技术,以利用从更广泛的分子集合中学到的知识,并将其应用于生成少研究或新化合物的构象。这可以显著减少数据需求,并提高模型的泛化能力。第三,现有方法主要集中在生成低能量构象,因为它们是稳定的。然而,探索高能量过渡态(TS)中的分子构象同样重要,因为它们对化学反应的进展至关重要[Choi 2023; Duan等,2023a]。因此,未来的研究也可以集中在生成反应物和产物的TS结构上,有助于更深入地理解化学反应的动力学和机制。解决这些方向将显著推动该领域的发展,并有助于开发更有效、高效和实际相关的分子构象生成方法。
5.4 从头开始生成分子 作者:Youzhi Luo,Minkai Xu,Stefano Ermon,Shuiwang Ji 推荐先决条件:第5.2节 在第5.2节中,我们研究了从给定分子预测性质的问题。然而,一些其他现实世界的问题,比如为药物设计新的分子,需要我们对反向过程建模,即在给定性质的情况下获得目标分子。在化学空间中穷尽地搜索目标分子是不可能的,因为候选分子的数量可能非常大,例如,估计有大约10^33个药物类似分子[Polishchuk et al. 2013]。最近,深度生成学习取得的显著进展已经激发了许多研究人员使用先进的深度生成模型生成新的分子,包括变分自编码器(VAEs)[Kingma和Welling 2014],生成对抗网络(GANs)[Goodfellow et al. 2014a],流模型[Rezende和Mohamed 2015]和扩散模型[Ho et al. 2020]。一些早期研究[Jin等人2018;You等人2018a;Shi等人2020]以2D分子图的形式生成分子。然而,这些方法不会生成分子中原子的3D坐标,因此不能区分具有相同2D图但不同3D几何结构的分子,例如空间异构体。实际上,许多分子性质,如量子性质或生物活性,是由分子的3D几何结构决定的。因此,在本节中,我们关注3D分子生成问题。 5.4.1 问题设置。 我们用𝑛个原子表示一个3D分子,表示为M=(𝒛,𝐶),其中𝒛=[𝑧,...,𝑧]∈Z𝑛是原子类型向量,𝐶=[𝒄1,...,𝒄𝑛]∈R3×𝑛是原子坐标矩阵。这里,对于第𝑖个原子,𝑧𝑖是其原子序数,𝒄𝑖是其3D笛卡尔坐标。我们的目标是使用生成模型学习3D分子空间上的概率分布𝑝,并从𝑝中采样新的3D分子。需要注意的是,与第5.3节讨论的分子构象生成或预测问题不同,我们不是从任何条件输入(如2D分子图)生成3D分子,而是从头开始生成它们。 5.4.2 技术挑战。 从头开始生成3D分子的核心挑战在于在生成3D原子位置时实现𝑆𝐸(3)不变性。换句话说,生成模型在3D空间中旋转或平移M后,应该为M和M'分配相同的概率。通常有两种策略生成3D分子结构。首先,生成模型可以直接使用坐标矩阵作为生成目标或输出。但挑战在于,坐标矩阵的概率建模必须经过精心设计,以确保对𝑆𝐸(3)变换具有不变性。其次,生成模型可以采用一些𝑆𝐸(3)不变的3D特征,例如距离或角度,作为生成目标。这种策略消除了在生成模型中明确考虑𝑆𝐸(3)不变性的必要性,但要求生成的3D特征具有有效的值和完整的3D结构信息,以便可以从中重建3D原子坐标。
5.4.3 现有方法。 直接生成3D分子坐标矩阵的三种代表性方法是E-NFs [Satorras等人2021b],EDM [Hoogeboom等人2022] 和GeoLDM [Xu等人2023a]。它们采用多种策略来实现𝐸(3)不变性,其中𝐸(3)是𝑆𝐸(3)的超集,包括平移、旋转和反射。具体来说,为了消除平移的自由度,任何3D分子都会在传递到生成模型之前通过从坐标矩阵的每一列中减去质心,即所有原子的平均3D坐标,来置零中心化。换句话说,这些方法捕获的概率密度仅在具有零质心的坐标矩阵上具有非零值。此外,零中心坐标的概率密度是通过它们对应的潜在变量计算的,这些潜在变量服从CoM-free高斯分布[Köhler等人2020]。从数学上讲,CoM-free高斯分布确保概率密度对旋转和反射是不变的。在E-NFs和EDM中,流和扩散模型用于将零中心坐标矩阵和潜在先验变量之间进行映射。GeoLDM进一步提出将零中心原子首先编码为零中心潜在空间,在这个空间中,每个原子都用潜在不变特征和潜在等变坐标表示。然后,GeoLDM不是学习将原始坐标矩阵映射到潜在变量,而是学习通过潜在扩散模型[Rombach等人2022]将潜在变量映射到先验高斯分布之间的映射。
与E-NFs和EDM不同,一些方法从𝑆𝐸(3)不变特征中隐式生成3D原子位置。为了表示3D分子的完整结构信息,替代坐标矩阵的一个选择是包含分子中每对原子之间距离的欧几里得距离矩阵。EDMNet [Hoffmann和Noé 2019] 是研究以欧几里得距离矩阵形式生成3D分子结构的第一个工作。在EDMNet中,使用各种新颖的损失函数来训练GAN模型,以生成有效的欧几里得距离矩阵,以便成功重建3D笛卡尔坐标。与EDMNet等一次性方法不同,其他方法采用自回归过程通过逐步将原子放置在3D空间中生成3D分子。自回归方法的两个代表是G-SchNet [Gebauer等人2019] 和G-SphereNet [Luo和Ji 2022]。在这两种方法中,通过多个步骤生成完整的3D分子,每个生成步骤只生成一个新原子,并将其放置在参考原子的局部区域。具体来说,G-SchNet通过从自回归生成模型预测的距离分布中采样,将新原子放置在参考原子的候选网格位置之一。另一方面,G-SphereNet通过自回归流模型生成距离、线角和扭角,以确定新原子相对于参考原子的相对位置。由于使用了扭角,G-SphereNet捕获了𝑆𝐸(3)不变分布。我们在表19中总结了讨论的3D分子生成方法的关键信息。需要注意的是,在讨论的这些方法中,只有EDM可以将分子性质作为条件输入并执行面向性质的生成,而其他方法只能使用隐式策略生成具有期望性质的分子,例如优化潜在表示。一些其他方法可能考虑更复杂的条件输入,例如蛋白质口袋[Ragoza等人2022;刘等人2022c],这将在第8节中介绍。
表19. 总结了几种代表性的3D分子生成方法的3D输出、模型架构、生成流程以及分布对称性。在这些方法中,E-NFs [Satorras等人2021b]、EDM [Hoogeboom等人2022] 和GeoLDM [Xu等人2023a] 直接生成分子中原子的3D坐标。它们通过将坐标置零中心化并使用CoM-free高斯分布来实现𝐸(3)不变性。另一方面,EDMNet [Hoffmann和Noé 2019]、G-SchNet [Gebauer等人2019] 和G-SphereNet [Luo和Ji 2022] 隐式生成原子的3D位置,这些位置是对旋转和平移不变的距离、角度和扭角计算得到的。

5.4.4 数据集和基准。
两个常用的基准数据集,QM9 [Ramakrishnan等人2014] 和GEOM-Drugs [Axelrod和Gómez-Bombarelli 2022],通常用于评估不同的3D分子生成方法的性能。QM9数据集从GDB-17 [Rud-digkeit等人2012] 数据库中收集了超过130k个小有机分子。QM9中的所有分子都有高达9个重原子(包括氢原子),并且任何重原子的元素类型始终是碳、氮、氧和氟中的一个。QM9中分子的3D原子坐标是通过Gaussian软件[Frisch等人2009]在B3LYP/6-31G (2df, p)量子化学水平下计算的。除了QM9外,GEOM-Drugs是另一个用于评估3D分子生成方法在生成更大更复杂的药物分子方面性能的数据集。它收集了高达181个原子的430k个类似药物的分子。GEOM-Drugs中分子的3D原子坐标首先由RDKit [Landrum 2010]初始化,然后通过ORCA [Neese 2012] 和CREST [Grimme 2019]软件进行优化。在这两个数据集中,分子中原子的3D坐标是通过DFT计算得到的。
5.4.5 开放研究方向。
尽管近年来已经提出了许多3D分子生成方法,但仍存在一些挑战,阻碍它们生成实际有用的3D分子。首先,大多数现有方法考虑𝐸(3)对称性,而不是𝑆𝐸(3)对称性,因此它们也对反射具有不变性。这种不变性在许多生物和化学应用中应该被避免,因为在这些应用中,生成模型应该能够区分具有不同手性的3D分子。此外,生成的3D分子要满足一些局部结构的3D位置的化学约束,以使它们在化学上有效且可合成。例如,苯环中的所有原子都受到限制,必须在同一个平面内。然而,设计满足所有化学约束的生成模型仍然具有挑战性,并且尚未充分研究。
5.5 分子动力学模拟 作者:Xiang Fu,Tommi Jaakkola 推荐先修知识:第5.2节 自从20世纪50年代开始发展以来,分子动力学(MD)模拟已经发展成为一种成熟且有价值的技术,用于深入了解各种物理和生物系统的原子层次的内部机制[Alder和Wainwright 1959; Rahman 1964; Frenkel和Smit 2001; Schlick 2010; Tuckerman 2010]。通过MD模拟,研究人员可以有效地表征系统下面的势能面(PES),并根据生成的MD轨迹计算基于宏观水平的可观测量。这些可观测量在确定重要材料特性(如电池材料的扩散性[Webb等人2015])和提供有关物理机制的宝贵见解(如蛋白质折叠动力学[Lane等人2011; Lindorff-Larsen等人2011])方面发挥着关键作用。然而,由于计算成本高昂,MD模拟的实际适用性受到限制。这种成本主要来自两个主要因素:首先,在许多需要高精度的应用中,必须使用量子化学方法来确定能量和力,这涉及到近似求解计算成本高昂的薛定谔方程(第4节)。其次,当研究大型复杂系统(如聚合物和蛋白质)时,通常需要进行广泛的模拟,跨越纳秒到毫秒的时间范围,以研究特定的物理过程,而数值稳定性所需的时间步长通常处于飞秒级别。进行这种模拟,即使使用精度较低的经典力场,也会产生大量的计算开销。近年来,机器学习(ML)方法显示出加速MD模拟的潜力。本节简要介绍了应用于MD模拟的ML方法的一些前沿,包括ML力场、ML增强采样方法和基于ML的粗粒化方法。尽管我们将这个小节分类为小分子的AI,但重要的是要注意,MD模拟是一种多功能的计算技术,适用于各种分子,包括小有机分子、生物大分子和材料。
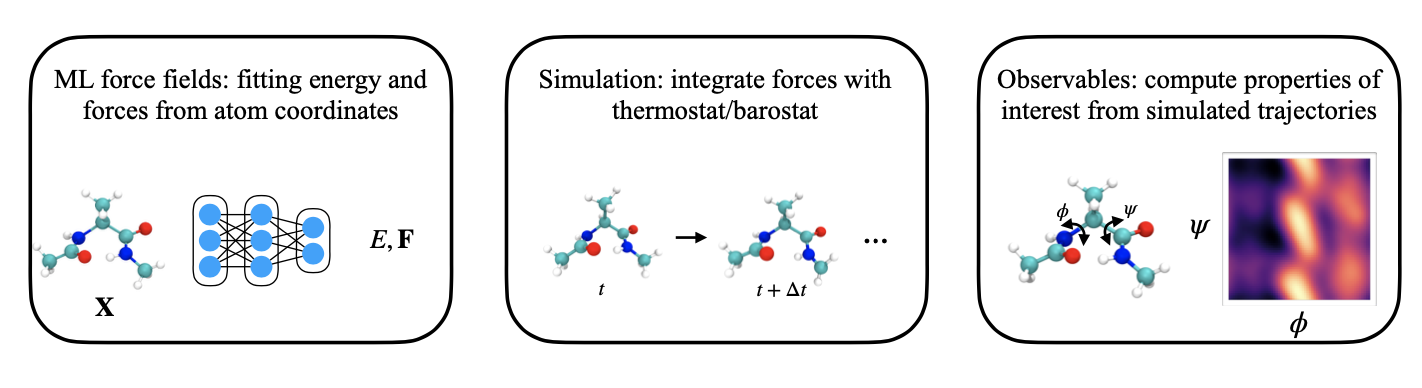
图21. 使用机器学习模拟分子动力学。为了替代昂贵的量子力学计算,学习了一个机器学习力场来预测原子坐标的能量和力。使用学习到的力场,我们可以通过与合适的恒温器/恒压器配对来模拟分子动力学。从模拟轨迹中,可以计算出感兴趣的性质。
5.5.1 问题设置。
模拟分子动力学涉及积分牛顿的运动方程:𝑑²𝒙 =𝒎−1𝑭(𝒙) . 𝑑𝑡²
这个积分所需的力是通过对势能函数进行微分获得的:𝑭(𝒙) = −𝜕𝐸(𝒙) . 这里,𝒙表示状态配置,𝒎表示原子的质量,𝜕𝒙
而𝐹和𝐸分别表示力和势能函数。为了复制所需的热力学条件,比如恒定温度或压力,需要选择一个合适的恒温器或恒压器,以通过附加变量增强运动方程。这些条件的选择取决于具体的系统和任务。通过模拟,生成了一系列时间序列的位置{𝒙𝑡 ∈ R𝑁 ×3 }𝑇𝑡 =0(和速度),其中𝑡表示时间顺序索引,𝑇表示模拟步骤的总数,𝑁是分子中的原子数。从时间序列中,可以计算出可观测量𝑂 (𝒙𝑡 ),如径向分布函数(RDFs)、虚拟应力张量、平均平方位移(MSD)和关于关键反应坐标的自由能面。这些可观测量在研究各种物理和生物系统的结构和动力学特性方面发挥着关键作用。图21总结了使用ML力场(FFs)来模拟MD轨迹的流程。
获取给定状态的力和能量需要经典或量子力学计算。虽然量子力学计算提供了更高的准确性,但计算成本高。为了加速MD模拟,一种策略是拟合一个机器学习(ML)模型,该模型从原子坐标预测𝐹 (𝒙) 和𝐸(𝒙)。这些模型被称为机器学习力场,它们经过训练以近似原子级别的力和能量,使用一个训练数据集:{𝒙𝑖,𝑭𝑖,𝐸𝑖}𝑁data,其中𝒙𝑖 ∈R𝑁×3,𝑭𝑖 ∈R𝑁×3,𝐸𝑖 ∈R,𝑁data是数据点的数量。学到的𝑖=1力场然后可以用来通过替换获取能量和力的计算成本高昂的量子力学计算来模拟分子动力学。
除了ML力场外,重要的是要注意,MD模拟的主要目标是提取表征系统性质的宏观可观测量。由于分子动力学的混沌性质,不必要也不实际地恢复初始状态的轨迹。因此,许多方法侧重于增强现有的力场,以实现更高效的采样或粗粒化,旨在降低系统的复杂性。采样和粗粒化方法的设计通常受到特定系统/可观测量的影响。
5.5.2 技术挑战。 首先,分子系统的势能面(PES)通常是高度不光滑的。复杂的原子相互作用需要有关原子环境的表达描述。理想情况下,应该尊重能量(𝐸(3)-不变)和力(𝐸(3)-等变)的物理对称性。具有表达能力的模型架构是设计准确的ML力场的关键技术问题。复杂的PES还在有效采样多样性构象方面提出了技术挑战,这激发了增强采样方法的研究。其次,虽然模拟时间步长通常在飞秒级别,但感兴趣的可观测量通常可以在更长的时间尺度上。因此,实际有用的MD轨迹需要模拟数百万到数十亿步以采样动态过程。这个实际需求对学到的力场的效率、稳定性和准确性提出了挑战。很难在没有实际运行昂贵的模拟的情况下预测在模拟环境中学到的力场的性能。最近的研究表明,更低的力/能量预测误差并不意味着模拟或可观测量计算更稳定和准确 [Fu et al. 2023a]。全原子MD模拟与感兴趣的实际可观测量之间的规模差异也激发了粗粒化方法的研究。特别是,稀有原子事件的采样是一个重要但困难的问题,因为上述两个挑战的结合:复杂的势能面可能在不同局部极小值之间有高能量壁垒,使得稀有事件(如不同亚稳态之间的转变)难以采样。因此,这些转变发生的时间尺度远远超出了学到的力场操作的时间尺度。总之,学习MD模拟的技术挑战根源于原子系统势能面的固有复杂性以及计算大时空尺度的能量和力的计算复杂性。
5.5.3 现有方法。
ML力场[Behler和Parrinello 2007; Khorshidi和Peterson 2016; Smith等2017; Artrith等2017; Chmiela等2017,2018; Zhang等2018a,b; Thomas等2018; Jia等2020; Gasteiger等2020; Schoenholz和Cubuk 2020; Noé等2020; Doerr等2021; Kovács等2021; Satorras等2021b; Unke等2021b; Park等2021; Thölke和Fabritiis 2022; Gasteiger等2021; Friederich等2021; Liu等2022f; Li等2022d; Batzner等2022; Takamoto等2022b; Musaelian等2023a]已经取得了令人难以置信的准确性和数据/计算效率,使它们在许多应用中有望取代量子力学计算。已经探索了不同的模型架构,包括基于核方法、前馈神经网络和消息传递神经网络。这些模型旨在尊重物理对称性原理,包括能量的𝐸(3)-不变性和力的𝐸(3)-等变性。许多分子表示学习研究受到了MD应用的激发,这些已在第5.2节中详细介绍。
为了增强采样过程,已经采用了机器学习(ML)方法来揭示关键的反应坐标[Sidky等2020a; Mehdi等2023](也称为集体变量)。这些坐标作为实施特定高级采样技术的先决条件,例如Meta Dynamics [Laio和Parrinello 2002; Barducci等2008]。确定反应坐标还可以在阐明分子动力学(MD)过程中发挥重要作用,特别是在拟合用于研究蛋白质分子中的亚稳态之间发生的转变的马尔可夫状态模型时[Mardt等2018]。此外,ML技术正在用于学习粗粒化力场[Husic等2020; Wang等2019b]、粗粒化和潜在空间模拟器[Fu等2022b; Vlachas等2021; Sidky等2020b]以及粗粒化映射[Wang和Gómez-Bombarelli 2019; Wang等2022l; Köhler等2023]。粗粒化空间中的模拟通常更加高效,但涉及准确性的权衡。学习粗粒化映射包括发现一种能够保留分子状态的基本信息并促进粗粒化反映(预测与粗粒化状态相对应的细粒化状态分布)的粗粒化方案的发现。
必须承认上述研究领域在各自领域中有着广泛的历史,并且继续积极发展。这里探讨的材料和参考资料仅提供了一个非常初步的概述。对于更深入的理解,我们建议感兴趣的读者参阅更详尽的调查报告,例如[Sidky等2020a; Unke等2021c; Noid 2023]。
5.5.4 数据集和基准。
小分子[Chmiela等2017,2023; Eastman等2023]一直是ML力场开发的热门测试平台。广泛使用的MD17数据集[Chmiela等2017]包含从路径积分分子动力学模拟生成的八种小分子的MD数据,还有使用更高级别理论更准确的MD17@CCSD(T)[Chmiela等2018]和rMD17[Christensen和Von Lilienfeld 2020]等更新版本。其他感兴趣的系统包括大块水[Zhang等2018a]、各种晶体固体材料(例如锂离子电解质[Batzner等2022])和非晶材料(例如聚合物[Fu等2022b])。使用这些数据集,现有工作中常见的基准策略是在测试数据集上的力和能量预测误差。一些论文[Stocker等2022; Zhang等2018a; Batzner等2022]还研究了模拟的稳定性和一些可观测量,如原子间距离分布、径向分布函数、扩散系数等等。特别是最近的一项基准研究[Fu等2023a]比较了一系列现有的ML力场在各种系统和任务上的表现,并发现了力/能量预测性能与模拟性能之间的不一致,显示了单独使用力和能量预测作为评估协议的无效性。
对于生物分子,现有研究的一个重点是根据关键反应坐标恢复它们的自由能面(FES)。丙氨酸二肽[Noé等2020]是标准的基准分子,因为它的反应坐标和FES已经得到很好的理解:有两个主要的构象自由度:C − N − C𝛼 − C的二面角𝜙和N − C𝛼 − C − N的二面角𝜓,这两个反应坐标上有六个FES极小值。已经有很多论文研究了采样Boltzmann分布[Fu等2023a]、过渡路径采样[Holdijk等2022]和粗粒度MD研究[Wang等2019b; Vlachas等2021; Greener和Jones 2021]。还研究了更复杂的生物分子,例如小蛋白质Chignolin[Husic等2020; Wang等2022l]。对于材料,过去的研究已经研究了锂离子电池电解质,例如LiPS[Batzner等2022]和固体聚合物电解质[Fu等2022b],同时关注径向分布函数和锂离子扩散率作为关键的可观测量。最后,我们注意到,MD模拟是一个涵盖广泛应用和数据集丰富的领域。我们只涵盖了一些使用ML方法研究的最流行的领域之一。
目前的机器学习(ML)力场的精度和效能为进一步改进提供了充分的机会。现有方法主要建立在基于核方法或通过预定半径截断形成的图上的消息传递方案之上。提高ML力场效能的有前途的途径是准确高效地捕捉长程相互作用。鉴于ML力场背后的主要动机是加速分子动力学(MD)模拟,设计重点关注计算效率和可并行化的神经架构,而不损害准确性,具有关键意义。例如,现有工作已经探讨了严格的局部ML势[Musaelian等2023a]。在实践中,应用ML力场时模拟不稳定性是一个经常出现的问题。专注于从学习模型性能不佳的状态收集新数据的主动学习策略[Vandermause等2020; Ang等2021]可以帮助解决这些不稳定性问题,并减少训练可靠ML力场所需的基础真相计算的数量。作为将MD模拟扩展到更广泛空间和时间尺度的关键途径,粗粒化方法在空间(通过将原子转化为粗粒化珠子)和时间(通过使用更大的时间步长,例如通过学习时间积分动力学)方面都非常重要。未来的研究应努力进一步理解和表征粗粒化(CG)方案中保留和放弃的信息。还必须探索如何创建更有效的CG方案,以在指定的计算预算内保留最大量的信息。最后,学习采样罕见事件的努力构成了另一个充满活力的研究领域。在这个领域,各种方法,如基于ML的集体变量发现[Sidky等2020a]、过渡路径采样[Holdijk等2022]和用于建模Boltzmann分布的深度生成模型[Noé等2019],代表了推进这一研究主题的有前途的方向。
学习立体异构和构象的3D图神经网络(GNNs)与其2D对应物相比的一个潜在优势是,它们可以本地模拟立体异构体之间的结构差异,这些分子在2D分子图中相同,但在3D中的原子排列不同。 立体异构通常由四面体手性中心(例如,具有四个非等价的键合邻居的碳原子),具有不同E/Z(顺/反)构型的双键以及带有手性轴的atropisomers,allenes或其他螺旋分子引起(图22)[Eliel and Wilen 1994]。值得注意的是,分子图可能具有许多不同的立体异构体;具有𝑁个四面体手性中心的分子可以有多达2𝑁个立体异构体,甚至不考虑E/Z异构体或轴手性。两个立体异构体可以被分类为非对映异构体或对映异构体。对映异构体是镜像的手性分子,不能通过热力学许可的构象变化(例如,化学键旋转)来重叠。非对映异构体通常具有完全不同的化学性质,而对映异构体在许多情况下具有相同的物理化学性质,除非与其他手性分子(如蛋白质)相互作用,在这种情况下,它们的性质可能会有很大不同[McConathy and Owens 2003; Chhabra et al. 2013]。因此,图神经网络学习立体异构的微妙影响的能力对于从药物化学到化学催化等各个领域的实际应用至关重要。由于分子属性预测所使用的大多数基准不需要仔细处理,因此立体异构曾经被忽视为分子身份的一部分,因为这些基准存在很高的随机不确定性,并且在数据集中立体异构体的表现不足。
构象异构还是立体化学的另一种形式,它描述了单一分子如何在潜在能量表面上采用许多不同的低能结构,统称为构象集合[Wolf 2007; Eliel and Wilen 1994]。第5.2节描述了静态和已知的3D分子结构上的表示学习,例如来自QM9数据集的DFT优化的基态分子几何构型[Ramakrishnan等人2014]。实际上,分子不是静态结构,而是通过分子内运动(如化学键旋转和较小的振动扰动)不断地在不同构象之间相互转化。这些运动的能量代价依赖于环境(例如,依赖于溶剂),而构象相互转化的速率高度依赖于温度。例如,在室温下,环己烷经历椅子翻转(能量障碍为10 kcal/mol),其特征周期为微秒[Hendrickson 1961],而像1,1'-联萘这样的庞大双芳基系统在小时级的时间尺度上在其(R)-和(S)-atropisomers之间相互转化(23 kcal/mol的能量障碍)[Meca等人2003]。俗称,如果两个构象不能在实际时间尺度上(例如,在室温下无法分离)在构象异构体之间进行热相互转化,那么两个构象将被认为属于不同的“立体异构体”;如果两个构象是互相可访问的,那么它们将被描述为对应于同一“立体异构体”。
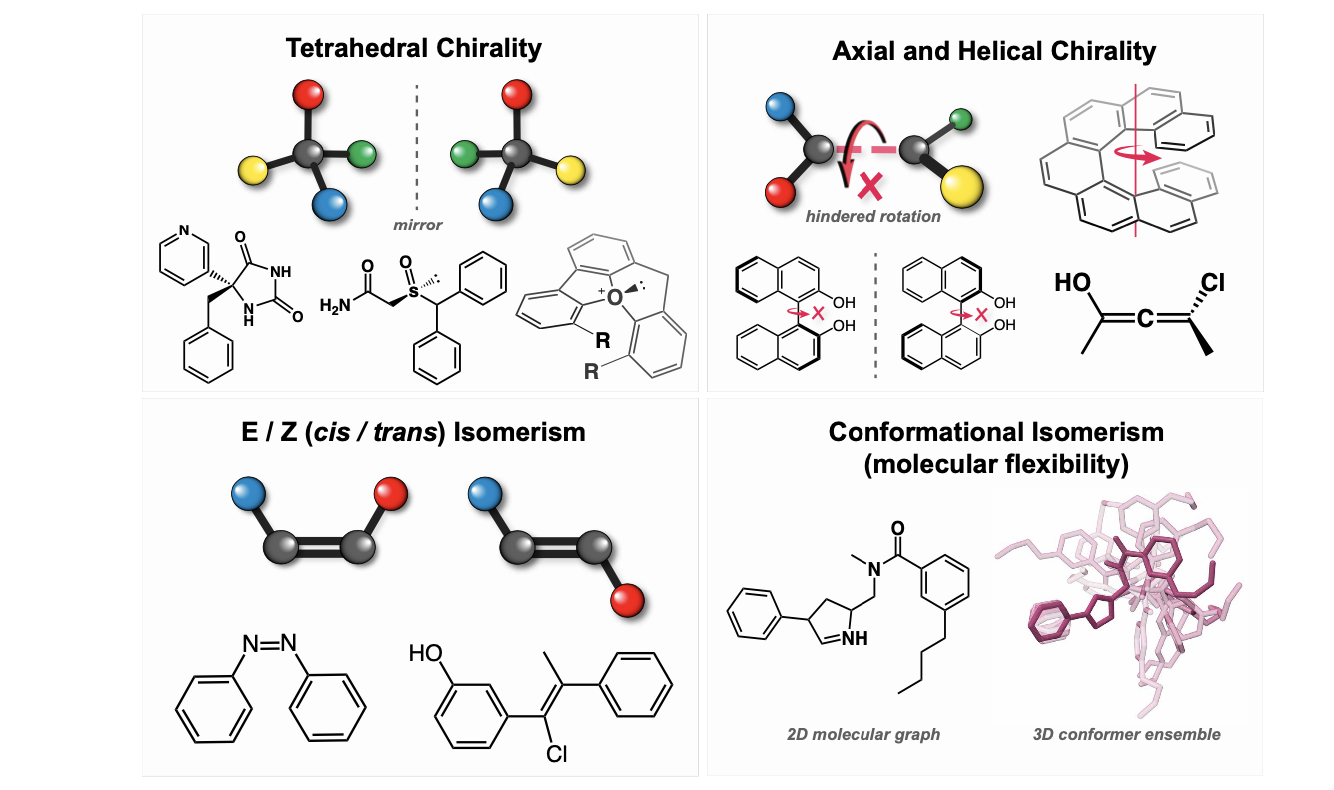
图22。立体化学是分子身份的一个重要但常常被忽视的方面,它描述了在三维空间中具有相同的二维图拓扑结构的分子的不同取向或排列。立体异构体可以由各种局部结构特征引起;这里显示了对药物化学、化学催化和有机化学特别相关的立体化学常见形式。四面体手性(或点手性)描述了围绕立体中心的四个非等效化学基团的不同取向。四面体手性在反射时会颠倒,因此会引发对映异构体。四面体手性通常与碳原子相关,但也可以在其他地方出现,例如在亚砜或氧离子化合物中。轴手性是由围绕手性轴的四个化学取代基的(非平面)取向引起的。轴手性在联烯中由于相邻双键的螺旋状排列而存在,并且通常在atropisomers中存在,其中庞大的取代基限制了关于单键(𝜎)的旋转。螺旋手性也是轴手性的一种形式,尽管其结构起源不同。与四面体手性一样,轴手性导致对映异构体。E/Z异构体是由于(平面)双键的不同顺式或反式配置引起的。与四面体或轴手性不同,E/Z异构体不产生对映异构体。这些立体化学形式通常产生不能在实际时间尺度上通过化学反应进行相互转化的立体异构体。任何给定的立体异构体也可以具有一系列结构不同但快速相互转化的构象异构体,或构象异构体,这归因于分子的三维灵活性。可观测的分子性质通常与整个构象异构体的热力学平均值相关。
许多可以实验观察到的化学性质依赖于热力学可访问构象的完整分布。另一方面,有些性质可能依赖于事先不知道的特定(高能量)几何构型,比如配体的活性结合位点。分子的势能面还可以受到分子间相互作用(例如与溶剂分子的相互作用)的显著改变,这使得在不进行代价高昂的模拟的情况下难以确定哪些分子结构对可观察性质有重要贡献。尽管3D图神经网络主要用于编码单个3D结构(第5.2节),但最近的研究尝试通过明确地编码构象系列来表示构象的灵活性[Axelrod和Gomez-Bombarelli 2020; Chuang和Keiser 2020]。这对于预测依赖于分布的分子性质可能具有影响,例如玻尔兹曼平均配体-蛋白结合亲和力[Miller和Dill 1997; Gilson和Zhou 2007];化学反应速率和选择性[Hansen等人2016; Guan等人2018];以及自由能的熵贡献[Mezei和Beveridge 1986; Chen等人2004]。
5.6.1 问题设置. 对于给定的2D分子图G = (𝒛, 𝐸),其中𝒛是原子类型的向量(例如原子序号),𝐸表示图的邻接矩阵,我们可以正式地将其热力学可访问的构象系列描述为一组CG = {𝐶𝑖} | CG |,其中每个不同的3D分子几何𝐶𝑖 ∈R3×𝑛都附带有(自由)能量。虽然构象系列实际上是一个连续的分布,但通常通过在任何𝐶𝑖和𝐶𝑗之间强加亚埃姆最小均方根距离(RMSD)阈值来用一组离散的构象来描述它,CG可以分成𝑆个不相交的子集,对应于每个分子图的构象分布,以便CG = C1 ∪C2 ∪...∪C𝑆。 G𝑘𝑘=1 GGGGG 确定哪些构象属于不相交的子集的决定可能有些主观,但通常基于它们在与手头应用相关的任何时间尺度上互相转化的能力。分布中的每个构象都可以分配一个统计学(玻尔兹曼)权重𝑝𝐶𝑠 = exp( −𝑒𝑖 )/Í𝑗 exp( −𝑒𝑗 ),对应于它在实验条件下的预期存在,其中𝑒是构象𝐶𝑠的(自由)能量,𝑘是玻尔兹曼常数,𝑇是温度。一些示例的立体化学表示学习任务包括将给定的构象分类为众多立体异构体中的一个,对属于不同立体异构体的构象的学习表示进行对比,或训练监督模型以从采样的构象中预测不可互转的立体异构体的性质。这最后一个监督学习任务旨在学习𝑓ˆ(𝐶𝑠 ∈ C𝑠 ;𝜽) ≈ 𝑓 (C𝑠 ),其中𝑓ˆ是带有权重𝜽的神经网络。与构象系列相关的任务包括从完整构象系列的小子集中预测玻尔兹曼平均性质〈𝑦〉 = Í 𝑝 𝑓 (𝐶𝑠 ) , 𝑘𝐵 𝑖 𝐶𝑖 𝑖 𝑘 𝑘=1 𝑘𝐵其中𝑓(𝐶𝑖)是每个构象的特性,或者在一组(非活动的)假构构象中识别活性构象中的具有活性的构象。
5.6.2 技术挑战。
学习分子立体化学和构象的灵活性带来了多方面的建模挑战。因为立体异构体具有相同的分子图,2D图神经网络在区分具有不同化学性质的立体异构体方面受到本质上的限制。通常,从业者会增加分子图的简单原子(节点)或键(边)特征,用于存储立体化学信息,例如手性中心的手性或双键的构型 [Yang et al. 2019]。然而,常用的特征(例如R/S手性原子标签)是全局性质,不符合局部图卷积 [Pattanaik et al. 2020],具有受限的表示学习能力 [Adams et al. 2021],并且不考虑所有形式的分子手性。3D图神经网络在根据它们的对称性质来表达某些立体化学时也可能受到限制。例如,许多数学上简单的具有𝐸(3)-不变特征的3D图神经网络不能区分镜像结构的对映异构体。因此,通常需要更复杂的网络,具有4体相互作用或等变特征,以从3D分子结构中稳健地表达手性 [Liu et al. 2022f; Gasteiger et al. 2021; Thomas et al. 2018]。此外,从单个3D结构𝐶𝑠中充分预测立体异构体的性质𝑓 (CG𝑠 )需要神经网络学习对3D构象的不变性,以避免混淆哪些构象属于哪些立体异构体 [Adams et al. 2021]。同时,同时编码多个构象(至少)会线性增加训练/推断的计算成本,同时也会使网络优化变得更加具有挑战性 [Axelrod and Gomez-Bombarelli 2020]。
对构象系列和分子灵活性进行建模还会引发与在推理时获得高质量构象系列的成本相关的附加挑战。换句话说,如果预测模型是使用从昂贵的量子化学或分子动力学模拟获得的构象进行训练的,那么在推理时可能需要相同的模拟,以避免领域漂移降低模型的准确性。另一方面,如果只对不忠实地表示地面真实构象的廉价构象进行编码,可能很难准确预测高质量构象的结构敏感性质。例如,已经观察到,将经过分子力学力场优化的构象编码以预测经过DFT优化的分子的基态量子性质,与直接使用地面真实构象相比,可能会导致模型准确性大幅下降 [Stärk et al. 2022a; Pinheiro et al. 2022]。类似地,如果只对从系列中随机抽样的非活动构象进行建模,可能难以准确预测未知的活性构象的性质(例如,在不事先知道相关配体姿势的情况下预测蛋白质-配体结合亲和力)。虽然使用2D图神经网络可能会规避获取高质量构象的挑战,但2D图神经网络通常无法充分学习对分子几何形状高度敏感的函数。
还存在与收集用于基准测试和模型开发的高质量数据集相关的挑战。当开发用于预测从模拟构象获得的分布相关性质的模型时,关键是要以足够高的理论水平进行详尽的构象模拟,以避免遗漏重要的(低能或具有活性的)构象或赋予不现实的几何结构不应有的统计权重。这些构象搜索理想情况下应在反映物理条件的情况下进行,例如考虑溶剂分子对PES的影响。此外,开发用于立体化学表示学习的新模型通常受到高质量数据集的限制,这些数据集同时包括以下内容:1)每个分子图的多个立体异构体的性质,2)对分子立体化学敏感的性质,以及3)信噪比高的性质。
5.6.3 现有方法。
分子立体化学的表示:现有工作主要集中在通过分子SMILES字符串中的特殊标记或通过2D分子图中的原子(节点)和键(边)属性来编码四面体手性,偶尔还包括E/Z(或顺反)异构体 [Yang et al. 2019]。SMILES字符串可以通过“@”和“@@”标记来本地存储四面体手性中心的手性,这些标记指示了邻近原子的顺时针(CW)或逆时针(CCW)排序(如字符串中提供的)。类似地,“\”和“/”标记可以存储双键的构型。因此,序列编码器(如变换器或循环神经网络)原则上可以表达这些形式的立体化学。任何使用节点和边属性的2D图神经网络都可以类似地包括二进制独热特征,用于存储四面体中心或双键周围的局部配置,基于指定的原子顺序。相关策略创建了使用在特定原子顺序下四面体体积的符号的图卷积核 [Liu et al. 2022g]。然而,使用对任意记账敏感的原子或键顺序会破坏图神经网络的排列不变性。与依赖于局部原子顺序不同,四面体手性中心的绝对R/S手性和双键的E/Z构型可以通过启发式的Cahn-Ingold-Prelog(CIP)规则进行编码,这些规则指定了相邻原子的全局优先级排序[Cahn et al.1966]。然而,对分子图进行小的编辑(例如,用硅原子替换碳原子)可以翻转这些全局原子/键标签的奇偶性,而不会显着改变3D分子几何结构(图23),可能使学到的立体化学表示非平滑。
[Figure 23: Figure illustrating how small changes in a molecular graph can flip the parity of global atom/bond tags while maintaining the same 3D geometry.]
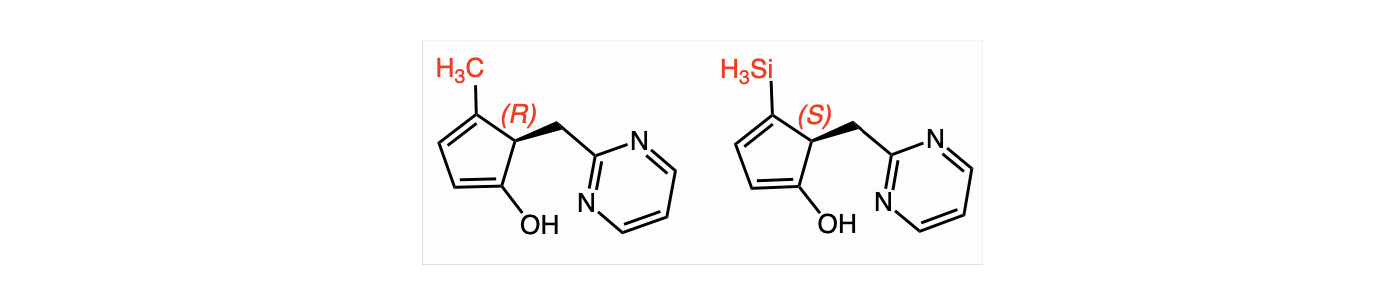
图23。 全局(R/S)手性原子标记不保留局部3D几何特征。 对分子图进行小的更改,例如将碳原子替换为硅原子,可以翻转四面体手性中心的手性(根据CIP规则),而不会影响3D分子几何结构或化学反应性。
Pattanaik等人[2020]和Adams等人[2021]引入了在图神经网络中编码四面体手性的替代方法,而无需使用启发式规则或破坏排列不变性。在GNN的每个消息传递层中,Pattanaik等人[2020]将求和池化操作(方程(92))更改为枚举和编码每个手性中心周围的四个相邻原子的所有12个排列,从而学习对四面体手性敏感的2D原子表示。Adams等人[2021]引入了ChIRo,通过特别编码每个内部化学键的二面角/扭转角,学习了四面体手性的3D表示。虽然模型需要输入一个构象体,但ChIRo本身对由键旋转引起的构象变化具有固有的不变性,研究表明使用由RDKit生成的廉价构象就足够了。这些方法在预测依赖手性的性质时经验性地表现出优越性,但以牺牲计算效率为代价。
𝑆𝐸(3)-不变的3D GNN,如SphereNet [Liu et al. 2022f],也可以学习对四面体手性敏感的表示。在这种情况下,重要的是在训练时使用每种分子的多个构象作为数据增强,以迫使网络学习一个近似构象不变性。然而,除了在计算上要求很高且需要训练很多构象之外,与仅使用具有手性原子标签的2D GNN相比,3D GNN在小分子的手性性质预测任务上表现不佳。
在构象集合上进行表示学习的最常见策略是将任务构建为多示例学习(MIL)问题[Dietterich等人,1997;Maron和Lozano-Pérez,1997;Ilse等人,2018]。在这种情况下,给定分子的多个构象实例分别编码为一组固定长度的嵌入,然后进行汇总或以其他方式聚合,以获得整个构象集合的单个嵌入。形式上,可以表示集合嵌入为
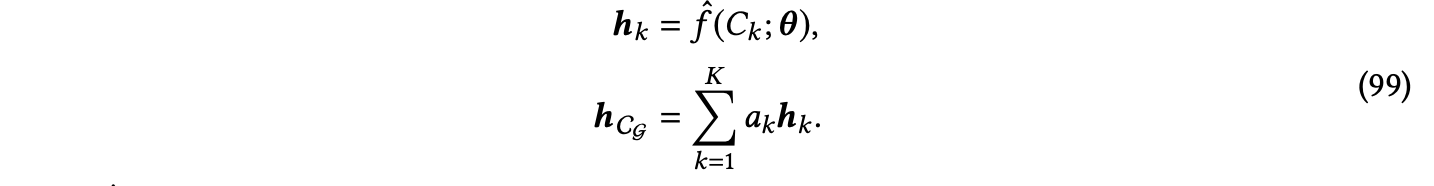
这里,𝑓ˆ(𝐶𝑘 ; 𝜽 ) 是任何机器学习模型,用于学习构象𝐶𝑘 的嵌入𝒉𝑘,例如3D GNN。例如,Axelrod和Gomez-Bombarelli[2020]使用了SchNet [Schütt等人,2018],并增加了额外的化学特征作为基础的3D GNN。许多其他使用MIL进行分子机器学习任务的工作使用非神经模型或手工制作的3D特征向量来编码𝒉𝑘 [Zahrt等人,2019;Zankov等人,2021;Weinreich等人,2021]。𝑎𝑘 可以设置为常数,以便在集合级表示𝒉 CG 中平等加权每个编码的构象,就像进行总和池化或均值池化一样。或者,𝑎𝑘 可以是学习的注意力系数,分配给每个编码的构象相对重要性,这可以用于识别集合中的关键构象实例,而无需预测实例级标签[Chuang和Keiser,2020]。另一种方法使用最大池化来聚合单个实例构象表示[Liu等人,2021a]。由于每个构象实例可能位于随机参考坐标系中,通常仅聚合𝑙 = 0不变表示(𝒉𝑘 = 𝒉𝑙=0)。
为了避免在推断时采样或编码多个构象的成本,其他工作尝试通过在结构空间中对多个构象进行平均来隐式建模构象的灵活性,通过在训练期间通过构象为基础的数据增强来学习构象不变性[Adams等人,2021],或通过在收集训练标签时考虑多个构象[Suriana等人,2023]。另一方面,不显式地从集合中编码单个构象可能会阻止模型识别关键构象实例,或者降低模型对重要的3D结构的敏感性。
表示分子立体化学:对映异构体具有共同的物理化学性质,如偶极矩或HOMO-LUMO能隙,这意味着为三维表示学习开发的流行基准,如QM9 [Ramakrishnan等人,2014]或PubChemQC [Nakata和Shimazaki,2017],即使这些数据集中的分子具有明确定义的手性,也不能用于评估模型学习手性敏感表示的能力。另一方面,蛋白质-配体结合亲和力或毒性测量等生物测量可能受到手性以及其他形式的立体化学的影响。然而,实验数据集,例如MoleculeNet [Wu等人,2018]中包含的数据集通常不包含同一分子的多个立体异构体的测量,因此不能直接评估模型是否学会了立体化学的影响。此外,手性的微妙影响可能会被实验噪声掩盖。因此,现有的工作在经过特殊策划以显示对分子立体化学,特别是四面体手性的急剧敏感的模拟数据集上对模型进行基准测试。
Pattanaik等人[2020]筛选了由Lyu等人[2019]执行的D4多巴胺受体蛋白质-配体对接筛选,策划了一个包含287,468个药物样分子的数据集,其中每个分子都具有至少一个四面体手性中心的Bemis-Murcko 1,3-二环己烷丙烷骨架。每个分子还被约束为在数据集中存在一对对映异构体或非对映异构体。他们进一步将该数据集分成一个子集,其中包含具有高于阈值的对接分数差异的对映异构体对,以及另一个子集,其中包含仅有一个手性中心的对映异构体对。Adams等人[2021]也使用受体-配体对接来评估具有手性感知模型。为了控制对接模拟中的随机性,他们将来自PubChem3D [Bolton等人,2011]的手性异构体对接到一个小的对接盒(PDB-ID:4JBV),这些手性异构体的分子量较低且可旋转键较少,并仅保留了在统计显着阈值以上的对接分数差异的34,560对手性异构体。在这两项工作中,模型根据其正确排列对映异构体对的能力来评估其预测的对接分数。
除了在模拟数据集上进行基准测试外,Adams等人[2021]和Mamede等人[2020]还精心策划了包含来自Reaxys数据库[Lawson等人,2014]的单手性中心对映异构体的实验测得的光学活性(“L”与“D”分类)的数据集。“L”与“D”的分类在作为基准任务时尤其有趣,因为光学活性难以在没有昂贵的从头计算的情况下模拟,L/D标签与R/S手性标签没有相关性,并且如果已知一对映异构体的光学旋转值,则可以直接推断另一对映异构体的光学旋转值。此外,预测光学活性在分配手性分子的绝对构型方面在实际中具有实用价值。我们设想,收集和公开传播包含感兴趣的手性敏感性质的类似数据集将有助于推动手性分子表示学习领域的发展。
对构象集合的表示学习:很少有数据集可以用来评估深度学习模型在预测构象集合的性质方面的性能,这是因为获取大量分子化合物的高质量构象集合及其相关性质所需的资源。Axelrod和Gomez-Bombarelli [2020]在278,758个药物样分子库中的生物活性样本中测试了一些2D、3D和3D-ensemble模型的分类能力,每个分子都有针对SARS-CoV 3CL蛋白酶的实验抑制数据注释。每个分子包含用CREST程序[Pracht等人,2020]生成的大量构象,用于构建编码包含多达200个构象的集合的模型。在这个任务上,明确编码多个构象的多实例集合的模型表现不如只编码单一构象的基线模型。MIL模型还需要更多数量级的资源来进行训练。值得注意的是,这个实验数据集非常不平衡,只包含426个生物活性样本,这可能会使模型优化变得复杂。Chuang和Keiser [2020]引入了一个小型合成数据集,包含最多一个可旋转键的1157个双芳基配体,每个配体包含平均13.8个由OMEGA [Hawkins等人,2010]生成的构象。他们评估了多实例注意模型识别编码的集合是否包含具有特定双齿协调几何的关键构象实例的能力。然而,在这个小玩具任务上,使用ECFP4分子指纹的简单随机森林基线模型优于MIL模型。
最近的研究已经创建了包含大量构象集合的新数据集,这些数据集有望用于构象集合学习。具体而言,Grambow等人[2023]介绍了CREMP数据集,其中包含使用CREST生成的36,198个大环肽的构象集合。Siebenmorgen等人[2023]介绍了MISATO,一个包含16,972个蛋白质-配体复合物的10纳秒分子动力学轨迹的数据集,这些复合物在明确的水溶剂中。
5.6.5 开放性研究方向。
设计下一代几何模型以更好地表示分子立体化学主要需要开发新的基准数据集,这些数据集包含每个分子的多个对映异构体,并标记有对立异构体敏感的性质。然而,在实际应用中,由于实验或计算预算的限制,收集每个分子的多个对映异构体的数据可能是不切实际的或不可行的。因此,另一个有前途的方向是设计可以在训练时学习对立异构体敏感性表示的模型或训练策略,而无需暴露于每个分子图中的多个对映异构体。此外,虽然当前的方法仅关注编码四面体手性,但未来的工作可以探索如何表示其他与药物相关的立体化学形式,如异构异构。
根据现有研究的有限数量,3D构象集合模型目前无法胜过只编码单一构象的传统3D模型,尽管构象集合中包含丰富的结构信息。未来的工作可以研究是否是由于现有研究中使用的过时3D模型架构,MIL框架无法捕捉构象的灵活性,或者同时编码结构多样性集合的模型优化困难,等等可能因素。在训练和推理过程中生成和编码多个构象的计算负担也对广泛采用MIL模型来编码构象集合提出了实际障碍。应该探索新的策略来高效考虑构象的灵活性。最后,由于在推理时使用物理上真实环境中的高质量构象集合通常对大规模虚拟屏幕来说是不切实际的,未来的工作可以研究模型的可转移性,这些模型可以编码从廉价算法或生成模型获得的现成构象集合。