一、简介
红黑树(Red-Black Tree)是一种自平衡的二叉搜索树,它的节点可以是红色或黑色。这个颜色的设计是为了满足红黑树的五个关键性质,确保树保持平衡和高效地支持插入、删除和搜索操作。
以下是红黑树的五个关键性质:
- 每个节点要么是红色,要么是黑色。
- 根节点是黑色的。
- 每个叶子节点(NIL节点,通常表示为黑色)是黑色的。
- 如果一个节点是红色的,那么它的两个子节点都是黑色的。
- 对于每个节点,从该节点到其后代任意叶子节点,经过的黑色节点的数量都相同。
这些性质确保了红黑树的平衡性,使得树的高度保持在可控范围内,从而保证了基本的搜索、插入和删除操作的时间复杂度为 O(log n),其中 n 是树中节点的数量。
红色节点和黑色节点的交替排列和上述性质的约束是为了保持树的平衡性。通过确保在树中的任何路径上都有相同数量的黑色节点,红黑树可以防止出现极端不平衡的情况,从而保证了树的高度保持在可控的范围内。红色节点的存在有助于确保在插入和删除节点时树能够重新平衡。
总之,红黑树中的红色节点和黑色节点是为了满足平衡性和其他性质而设计的,它们共同确保了红黑树的高效性和可预测性。
二、红黑树的操作
首先我们来看一个红黑树(红节点H,M也有叶子节点NIL没有画出了):
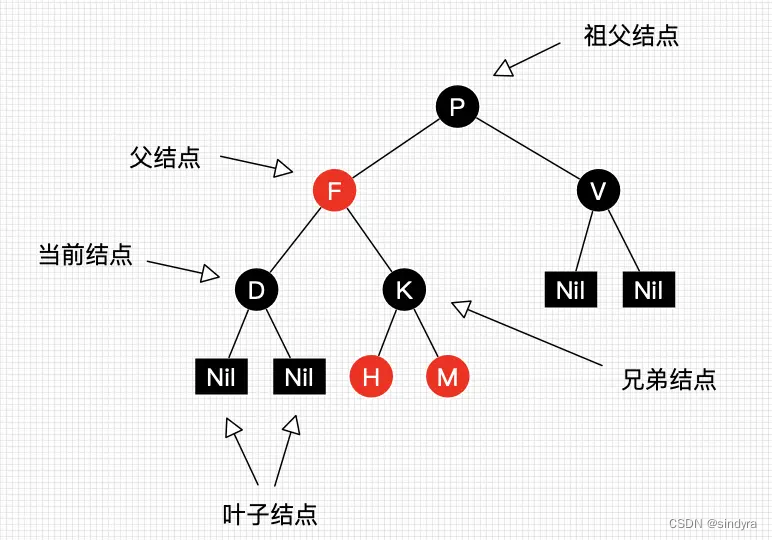
由此可见,红黑树并不是一个完美平衡二叉查找树,根结点P的左子树显然比右子树高,但左子树和右子树的黑结点的层数是相等的,也即任意一个结点到到每个叶子结点的路径都包含数量相同的黑结点(性质5)。所以我们叫红黑树这种平衡为黑色完美平衡。
由于红节点总是插入在黑节点中,所以左子树与右子树最大的差距也不会超过2倍,这就保证了树的平衡性。
例如 :黑-红-黑-红-黑 跟 黑-黑-黑,长度分别为5跟3,即5/3约等于1.6倍,显然没有超过2倍。
前面讲到红黑树能自平衡,它靠的是什么操作?三种操作:左旋、右旋和变色。
- 左旋:以某个结点作为支点(旋转结点),其右子结点变为旋转结点的父结点,右子结点的左子结点变为旋转结点的右子结点,左子结点保持不变。如图3。
- 右旋:以某个结点作为支点(旋转结点),其左子结点变为旋转结点的父结点,左子结点的右子结点变为旋转结点的左子结点,右子结点保持不变。如图4。
- 变色:结点的颜色由红变黑或由黑变红。
三、实现
using System;
public enum NodeColor
{
Red,
Black
}
public class Node
{
public int Data { get; set; }
public Node Parent { get; set; }
public Node Left { get; set; }
public Node Right { get; set; }
public NodeColor Color { get; set; }
}
public class RedBlackTree
{
private Node root;
// 插入节点
public void Insert(int data)
{
var node = new Node { Data = data, Color = NodeColor.Red };
if (root == null)
{
root = node;
root.Color = NodeColor.Black;
}
else
{
InsertNode(root, node);
FixTree(node);
}
}
// 辅助方法:插入节点
private void InsertNode(Node root, Node newNode)
{
if (newNode.Data < root.Data)
{
if (root.Left == null)
{
root.Left = newNode;
newNode.Parent = root;
}
else
InsertNode(root.Left, newNode);
}
else
{
if (root.Right == null)
{
root.Right = newNode;
newNode.Parent = root;
}
else
InsertNode(root.Right, newNode);
}
}
// 辅助方法:修复红黑树性质
private void FixTree(Node node)
{
while (node != root && node.Parent.Color == NodeColor.Red)
{
if (node.Parent == node.Parent.Parent.Left)
{
var uncle = node.Parent.Parent.Right;
if (uncle != null && uncle.Color == NodeColor.Red)
{
node.Parent.Color = NodeColor.Black;
uncle.Color = NodeColor.Black;
node.Parent.Parent.Color = NodeColor.Red;
node = node.Parent.Parent;
}
else
{
if (node == node.Parent.Right)
{
node = node.Parent;
RotateLeft(node);
}
node.Parent.Color = NodeColor.Black;
node.Parent.Parent.Color = NodeColor.Red;
RotateRight(node.Parent.Parent);
}
}
else
{
var uncle = node.Parent.Parent.Left;
if (uncle != null && uncle.Color == NodeColor.Red)
{
node.Parent.Color = NodeColor.Black;
uncle.Color = NodeColor.Black;
node.Parent.Parent.Color = NodeColor.Red;
node = node.Parent.Parent;
}
else
{
if (node == node.Parent.Left)
{
node = node.Parent;
RotateRight(node);
}
node.Parent.Color = NodeColor.Black;
node.Parent.Parent.Color = NodeColor.Red;
RotateLeft(node.Parent.Parent);
}
}
}
root.Color = NodeColor.Black;
}
// 左旋
private void RotateLeft(Node node)
{
var temp = node.Right;
node.Right = temp.Left;
if (temp.Left != null)
temp.Left.Parent = node;
if (temp != null)
temp.Parent = node.Parent;
if (node.Parent == null)
root = temp;
else if (node == node.Parent.Left)
node.Parent.Left = temp;
else
node.Parent.Right = temp;
temp.Left = node;
if (node != null)
node.Parent = temp;
}
// 右旋
private void RotateRight(Node node)
{
var temp = node.Left;
node.Left = temp.Right;
if (temp.Right != null)
temp.Right.Parent = node;
if (temp != null)
temp.Parent = node.Parent;
if (node.Parent == null)
root = temp;
else if (node == node.Parent.Right)
node.Parent.Right = temp;
else
node.Parent.Left = temp;
temp.Right = node;
if (node != null)
node.Parent = temp;
}
// 中序遍历
public void InOrderTraversal(Node node)
{
if (node != null)
{
InOrderTraversal(node.Left);
Console.WriteLine(node.Data + " " + node.Color);
InOrderTraversal(node.Right);
}
}
}
参考博客:https://www.jianshu.com/p/e136ec79235c