---

一、学习要点

  理解递归的概念。
  掌握设计有效算法的分治策略。
  通过下面的范例学习分治策略设计技巧。
  （1）二分搜索技术；
  （2）大整数乘法；
  （3）Strassen矩阵乘法；
  （4）棋盘覆盖；
  （5）合并排序和快速排序；
  （6）线性时间选择；
  （7）最接近点对问题；
  （8）循环赛日程表。

---

二、算法总体思想

  对这k个子问题分别求解。如果子问题的规模仍然不够小，则 再划分为k个子问题，如此递归的进行下去，直到问题规模足够小，很容易求出其解为止。

  将求出的小规模的问题的解合并为一个更大规模的问题的解，自底向上逐步求出原来问题的解。

  分治法的设计思想是，将一个难以直接解决的大问题，分割成一些规模较小的相同问题，以便各个击破，分而治之。

---

三、递归的概念

  直接或间接地调用自身的算法称为递归算法。用函数自身给出定义的函数称为递归函数。
  由分治法 产生的子问题往往是原问题的较小模式，这就为使用递归技术提供了方便。在这种情况下，反复应用分治手段，可以使子问题与原问题类型一致而其规模却不断缩小，最终使子问题缩小到很容易直接求出其解。这自然导致递归过程的产生。
  分治与递归像一对孪生兄弟，经常同时应用在算法设计之中，并由此产生许多高效算法。

---

例1 阶乘函数

  阶乘函数可递归地定义为：

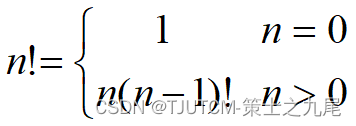
  边界条件与递归方程是递归函数的二个要素，递归函数只有具备了这两个要素，才能在有限次计算后得出结果。

---

例2 Fibonacci数列

  无穷数列1，1，2，3，5，8，13，21，34，55，……，称为Fibonacci数列。它可以递归地定义为：

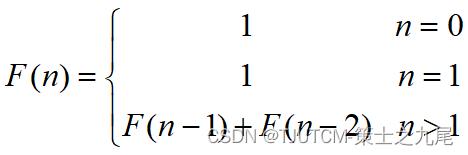
  第n个Fibonacci数可递归地计算如下：

int fibonacci(int n)
   {
       if (n <= 1) return 1;
       return fibonacci(n-1)+fibonacci(n-2);
   }

---

例3 Ackerman函数

  当一个函数及它的一个变量是由函数自身定义时，称这个函数是双递归函数。
  Ackerman函数A(n，m)定义如下：

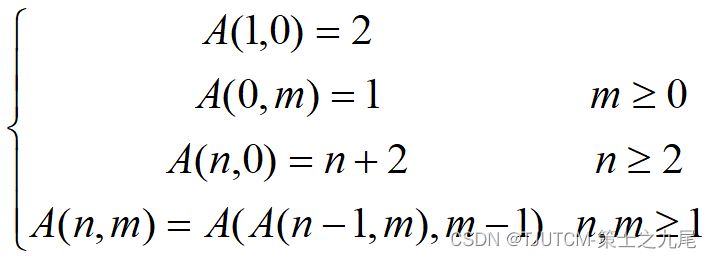
  前2例中的函数都可以找到相应的非递归方式定义：


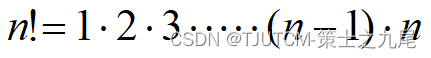
  本例中的Ackerman函数却无法找到非递归的定义。
  A(n，m)的自变量m的每一个值都定义了一个单变量函数：
  M=0时，A(n,0)=n+2
  M=1时，A(n,1)=A(A(n-1,1),0)=A(n-1,1)+2，和A(1,1)=2故A(n,1)=2*n
  M=2时，A(n,2)=A(A(n-1,2),1)=2A(n-1,2)，和A(1,2)=A(A(0,2),1)=A(1,1)=2，故A(n,2)= 2^n 。
  M=3时，类似的可以推出：

  M=4时，A(n,4)的增长速度非常快，以至于没有适当的数学式子来表示这一函数。
  定义单变量的Ackerman函数A(n)为，A(n)=A(n，n)。
  定义其拟逆函数α(n)为：α(n)=min{k｜A(k)≥n}。即α(n)是使n≤A(k)成立的最小的k值。
  α(n)在复杂度分析中常遇到。对于通常所见到的正整数n，有α(n)≤4。但在理论上α(n)没有上界，随着n的增加，它以难以想象的慢速度趋向正无穷大。

---

例4 整数划分问题

  将正整数n表示成一系列正整数之和：n=n1+n2+…+nk，其中n1≥n2≥…≥nk≥1，k≥1。
  正整数n的这种表示称为正整数n的划分。求正整数n的不同划分个数 。
  例如正整数6有如下11种不同的划分：
  6；
  5+1；
  4+2，4+1+1；
  3+3，3+2+1，3+1+1+1；
  2+2+2，2+2+1+1，2+1+1+1+1；
  1+1+1+1+1+1。
  前面的几个例子中，问题本身都具有比较明显的递归关系，因而容易用递归函数直接求解。
  在本例中，如果设p(n)为正整数n的划分数，则难以找到递归关系，因此考虑增加一个自变量：将最大加数n1不大于m的划分个数记作q(n,m)。可以建立q(n,m)的如下递归关系。
  (3) q(n,n)=1+q(n,n-1);
  正整数n的划分由n1=n的划分和n1≤n-1的划分组成。
  (4) q(n,m)=q(n,m-1)+q(n-m,m),n>m>1;
  正整数n的最大加数n1不大于m的划分由n1=m的划分和n1≤n-1 的划分组成。

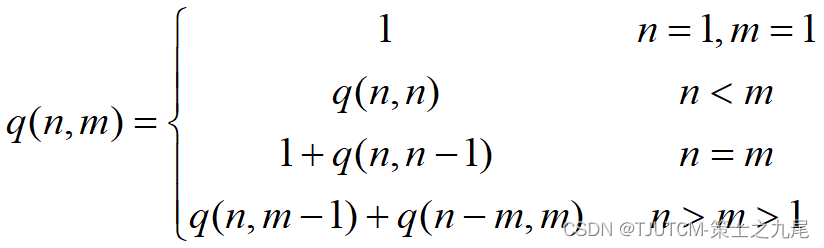
  正整数n的划分数p(n)=q(n,n)。

---

例5 Hanoi塔问题

  设a,b,c是3个塔座。开始时，在塔座a上有一叠共n个圆盘，这些圆盘自下而上，由大到小地叠在一起。各圆盘从小到大编号为1,2,…,n,现要求将塔座a上的这一叠圆盘移到塔座b上，并仍按同样顺序叠置。在移动圆盘时应遵守以下移动规则：
  规则1：每次只能移动1个圆盘；
  规则2：任何时刻都不允许将较大的圆盘压在较小的圆盘之上；
  规则3：在满足移动规则1和2的前提下，可将圆盘移至a,b,c中任一塔座上。

void hanoi(int n, int a, int b, int c)
   {
       if (n > 0)
       {
          hanoi(n-1, a, c, b);
          move(a,b);
          hanoi(n-1, c, b, a);
       }
   }

---

递归小结

  优点：结构清晰，可读性强，而且容易用数学归纳法来证明算法的正确性，因此它为设计算法、调试程序带来很大方便。
  缺点：递归算法的运行效率较低，无论是耗费的计算时间还是占用的存储空间都比非递归算法要多。
  解决方法：在递归算法中消除递归调用，使其转化为非递归算法。
  1、采用一个用户定义的栈来模拟系统的递归调用工作栈。该方法通用性强，但本质上还是递归，只不过人工做了本来由编译器做的事情，优化效果不明显。
  2、用递推来实现递归函数。
  3、通过变换能将一些递归转化为尾递归，从而迭代求出结果。
  后两种方法在时空复杂度上均有较大改善，但其适用范围有限。

---

四、分治法

1、分治法的适用条件

  分治法所能解决的问题一般具有以下几个特征：
  该问题的规模缩小到一定的程度就可以容易地解决；
  该问题可以分解为若干个规模较小的相同问题，即该问题具有最优子结构性质利用该问题分解出的子问题的解可以合并为该问题的解；
  该问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子问题。
  这条特征涉及到分治法的效率，如果各子问题是不独立的，则分治法要做许多不必要的工作，重复地解公共的子问题，此时虽然也可用分治法，但一般用动态规划较好。

divide-and-conquer(P)
  {
    if ( | P | <= n0) adhoc(P);   //解决小规模的问题
    divide P into smaller subinstances P1,P2,...,Pk；//分解问题
    for (i=1,i<=k,i++)
      yi=divide-and-conquer(Pi);  //递归的解各子问题
    return merge(y1,...,yk);  //将各子问题的解合并为原问题的解
  }

  人们从大量实践中发现，在用分治法设计算法时，最好使子问题的规模大致相同。即将一个问题分成大小相等的k个子问题的处理方法是行之有效的。这种使子问题规模大致相等的做法是出自一种平衡(balancing)子问题的思想，它几乎总是比子问题规模不等的做法要好。
  一个分治法将规模为n的问题分成k个规模为n／m的子问题去解。设分解阀值n0=1，且adhoc解规模为1的问题耗费1个单位时间。再设将原问题分解为k个子问题以及用merge将k个子问题的解合并为原问题的解需用f(n)个单位时间。用T(n)表示该分治法解规模为|P|=n的问题所需的计算时间，则有：

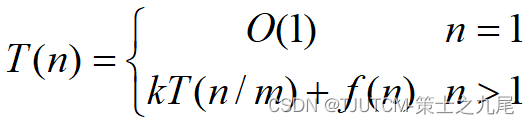
  通过迭代法求得方程的解：

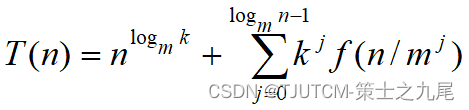
  注意：递归方程及其解只给出n等于m的方幂时T(n)的值，但是如果认为T(n)足够平滑，那么由n等于m的方幂时T(n)的值可以估计T(n)的增长速度。通常假定T(n)是单调上升的，从而当mi≤n<mi+1时，T(mi)≤T(n)<T(mi+1)。

---

2、二分搜索技术

  给定已按升序排好序的n个元素a[0:n-1]，现要在这n个元素中找出一特定元素x。
  分析：
  该问题的规模缩小到一定的程度就可以容易地解决；
  该问题可以分解为若干个规模较小的相同问题;
  分解出的子问题的解可以合并为原问题的解；
  分解出的各个子问题是相互独立的。
  分析：很显然此问题分解出的子问题相互独立，即在a[i]的前面或后面查找x是独立的子问题，因此满足分治法的第四个适用条件。
  据此容易设计出二分搜索算法：

template<class Type> 
int BinarySearch(Type a[], const Type& x, int l, int r)
{
     while (r >= l){ 
        int m = (l+r)/2;
        if (x == a[m]) return m;
        if (x < a[m]) r = m-1; else l = m+1;
        }
    return -1;
} 

  算法复杂度分析：
  每执行一次算法的while循环， 待搜索数组的大小减少一半。因此，在最坏情况下，while循环被执行了O(logn) 次。循环体内运算需要O(1) 时间，因此整个算法在最坏情况下的计算时间复杂性为O(logn)。

---

3、大整数的乘法

  请设计一个有效的算法，可以进行两个n位大整数的乘法运算。
  小学的方法：O(n2) ×效率太低
  分治法:


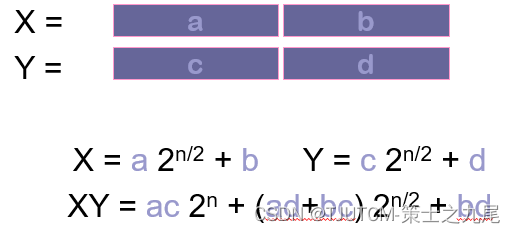
  XY = ac 2n + ((a-b)(d-c)+ac+bd) 2n/2 + bd
  XY = ac 2n + ((a+b)(c+d)-ac-bd) 2n/2 + bd
  细节问题：两个XY的复杂度都是O(nlog3)，但考虑到a+b,c+d可能得到m+1位的结果，使问题的规模变大，故不选择第2种方案。

  小学的方法：O(n2)   ×效率太低
  分治法: O(n1.59)   √较大的改进
  
  如果将大整数分成更多段，用更复杂的方式把它们组合起来，将有可能得到更优的算法。
  最终的，这个思想导致了快速傅利叶变换(Fast Fourier Transform)的产生。该方法也可以看作是一个复杂的分治算法。

---

4、Strassen矩阵乘法

  传统方法：O(n3)

  若依此定义来计算A和B的乘积矩阵C，则每计算C的一个元素C[i][j]，需要做n次乘法和n-1次加法。因此，算出矩阵C的 个元素所需的计算时间为O(n3)
  使用与上例类似的技术，将矩阵A，B和C中每一矩阵都分块成4个大小相等的子矩阵。由此可将方程C=AB重写为：

  由此可得：


  传统方法：O(n3)
  分治法:
  为了降低时间复杂度，必须减少乘法的次数。



  传统方法：O(n3)
  分治法: O(n2.81)
  更快的方法??
  Hopcroft和Kerr已经证明(1971)，计算2个２×２矩阵的乘积，7次乘法是必要的。因此，要想进一步改进矩阵乘法的时间复杂性，就不能再基于计算2×2矩阵的7次乘法这样的方法了。或许应当研究３×３或５×５矩阵的更好算法。
  在Strassen之后又有许多算法改进了矩阵乘法的计算时间复杂性。目前最好的计算时间上界是 O(n2.376)
  是否能找到O(n2)的算法？

---

5、棋盘覆盖

  在一个2k×2k 个方格组成的棋盘中，恰有一个方格与其它方格不同，称该方格为一特殊方格，且称该棋盘为一特殊棋盘。在棋盘覆盖问题中，要用图示的4种不同形态的L型骨牌覆盖给定的特殊棋盘上除特殊方格以外的所有方格，且任何2个L型骨牌不得重叠覆盖。


  当k>0时，将2k×2k棋盘分割为4个2k-1×2k-1 子棋盘(a)所示。
  特殊方格必位于4个较小子棋盘之一中，其余3个子棋盘中无特殊方格。为了将这3个无特殊方格的子棋盘转化为特殊棋盘，可以用一个L型骨牌覆盖这3个较小棋盘的会合处，如 (b)所示，从而将原问题转化为4个较小规模的棋盘覆盖问题。递归地使用这种分割，直至棋盘简化为棋盘1×1。

void chessBoard(int tr, int tc, int dr, int dc, int size){
      if (size == 1) return;
      int t = tile++,  // L型骨牌号
        s = size/2;  // 分割棋盘
      // 覆盖左上角子棋盘
      if (dr < tr + s && dc < tc + s)
         // 特殊方格在此棋盘中
         chessBoard(tr, tc, dr, dc, s);
      else {// 此棋盘中无特殊方格
         // 用 t 号L型骨牌覆盖右下角
         board[tr + s - 1][tc + s - 1] = t;
         // 覆盖其余方格
         chessBoard(tr, tc, tr+s-1, tc+s-1, s);}
      // 覆盖右上角子棋盘
      if (dr < tr + s && dc >= tc + s)
         // 特殊方格在此棋盘中
         chessBoard(tr, tc+s, dr, dc, s);
      else {// 此棋盘中无特殊方格
         // 用 t 号L型骨牌覆盖左下角
            board[tr + s - 1][tc + s] = t;
         // 覆盖其余方格
         chessBoard(tr, tc+s, tr+s-1, tc+s, s);}
        // 覆盖左下角子棋盘
      if (dr >= tr + s && dc < tc + s)
         // 特殊方格在此棋盘中
         chessBoard(tr+s, tc, dr, dc, s);
      else {// 用 t 号L型骨牌覆盖右上角
         board[tr + s][tc + s - 1] = t;
         // 覆盖其余方格
         chessBoard(tr+s, tc, tr+s, tc+s-1, s);}
      // 覆盖右下角子棋盘
      if (dr >= tr + s && dc >= tc + s)
         // 特殊方格在此棋盘中
         chessBoard(tr+s, tc+s, dr, dc, s);
      else {// 用 t 号L型骨牌覆盖左上角
         board[tr + s][tc + s] = t;
         // 覆盖其余方格
         chessBoard(tr+s, tc+s, tr+s, tc+s, s);}
   }   

  T(n)=O(4k) 渐进意义下的最优算法

---

6、合并排序

  基本思想：将待排序元素分成大小大致相同的2个子集合，分别对2个子集合进行排序，最终将排好序的子集合合并成为所要求的排好序的集合。

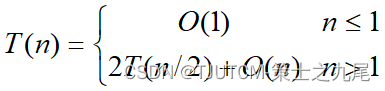
  T(n)=O(nlogn) 渐进意义下的最优算法

void MergeSort(Type a[], int left, int right)
   {
      if (left<right) {//至少有2个元素
      int i=(left+right)/2;  //取中点
      mergeSort(a, left, i);
      mergeSort(a, i+1, right);
      merge(a, b, left, i, right);  //合并到数组b
      copy(a, b, left, right);    //复制回数组a
      }
   }

  算法mergeSort的递归过程可以消去。

  最坏时间复杂度：O(nlogn)
  平均时间复杂度：O(nlogn)
  辅助空间：O(n)

---

7、快速排序

  在快速排序中，记录的比较和交换是从两端向中间进行的，关键字较大的记录一次就能交换到后面单元，关键字较小的记录一次就能交换到前面单元，记录每次移动的距离较大，因而总的比较和移动次数较少。

template<class Type>
void QuickSort (Type a[], int p, int r)
{
      if (p<r) {
        int q=Partition(a,p,r);
        QuickSort (a,p,q-1); //对左半段排序
        QuickSort (a,q+1,r); //对右半段排序
        }
}

template<class Type>
int Partition (Type a[], int p, int r)
{
        int i = p, j = r + 1; 
        Type x=a[p];
        // 将< x的元素交换到左边区域
        // 将> x的元素交换到右边区域
        while (true) {
           while (a[++i] <x);
           while (a[- -j] >x);
           if (i >= j) break; 
           Swap(a[i], a[j]);
           }
       a[p] = a[j];
       a[j] = x;
       return j;
}

  快速排序算法的性能取决于划分的对称性。通过修改算法partition，可以设计出采用随机选择策略的快速排序算法。在快速排序算法的每一步中，当数组还没有被划分时，可以在a[p:r]中随机选出一个元素作为划分基准，这样可以使划分基准的选择是随机的，从而可以期望划分是较对称的。

template<class Type>
int RandomizedPartition (Type a[], int p, int r)
{
        int i = Random(p,r);
        Swap(a[i], a[p]);
        return Partition (a, p, r);
}

---

8、线性时间选择

  给定线性序集中n个元素和一个整数k，1≤k≤n，要求找出这n个元素中第k小的元素。

template<class Type>
Type RandomizedSelect(Type a[],int p,int r,int k)
{
      if (p==r) return a[p];
      int i=RandomizedPartition(a,p,r),
      j=i-p+1;
      if (k<=j) return RandomizedSelect(a,p,i,k);
      else return RandomizedSelect(a,i+1,r,k-j);
}

  在最坏情况下，算法randomizedSelect需要O(n2)计算时间
  但可以证明，算法randomizedSelect可以在O(n)平均时间内找出n个输入元素中的第k小元素。
  如果能在线性时间内找到一个划分基准，使得按这个基准所划分出的2个子数组的长度都至少为原数组长度的ε倍(0<ε<1是某个正常数)，那么就可以在最坏情况下用O(n)时间完成选择任务。
  例如，若ε=9/10，算法递归调用所产生的子数组的长度至少缩短1/10。所以，在最坏情况下，算法所需的计算时间T(n)满足递归式T(n)≤T(9n/10)+O(n) 。由此可得T(n)=O(n)。

  将n个输入元素划分成n/5个组，每组5个元素，只可能有一个组不是5个元素。用任意一种排序算法，将每组中的元素排好序，并取出每组的中位数，共n/5个。
  递归调用select来找出这n/5个元素的中位数。如果n/5是偶数，就找它的2个中位数中较大的一个。以这个元素作为划分基准。

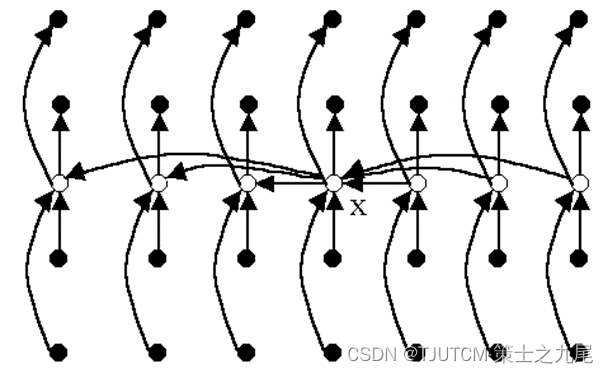
  设所有元素互不相同。在这种情况下，找出的基准x至少比3(n-5)/10个元素大，因为在每一组中有2个元素小于本组的中位数，而n/5个中位数中又有(n-5)/10个小于基准x。同理，基准x也至少比3(n-5)/10个元素小。而当n≥75时，3(n-5)/10≥n/4所以按此基准划分所得的2个子数组的长度都至少缩短1/4。

Type Select(Type a[], int p, int r, int k)
{
      if (r-p<75) {
        用某个简单排序算法对数组a[p:r]排序;
        return a[p+k-1];
        };
      for ( int i = 0; i<=(r-p-4)/5; i++ )
         将a[p+5*i]至a[p+5*i+4]的第3小元素
         与a[p+i]交换位置;
      //找中位数的中位数，r-p-4即上面所说的n-5
      Type x = Select(a, p, p+(r-p-4)/5, (r-p-4)/10);
      int i=Partition(a,p,r, x),
      j=i-p+1;
      if (k<=j) return Select(a,p,i,k);
      else return Select(a,i+1,r,k-j);
}

  上述算法将每一组的大小定为5，并选取75作为是否作递归调用的分界点。这2点保证了T(n)的递归式中2个自变量之和n/5+3n/4=19n/20=εn，0<ε<1。这是使T(n)=O(n)的关键之处。当然，除了5和75之外，还有其他选择。

---

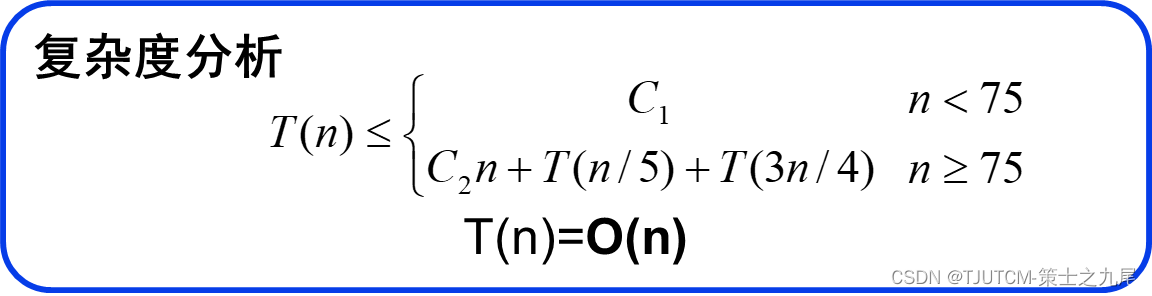
9、最接近点对问题

  为了使问题易于理解和分析，先来考虑一维的情形。此时，S中的n个点退化为x轴上的n个实数 x1,x2,…,xn。最接近点对即为这n个实数中相差最小的2个实数。
  假设我们用x轴上某个点m将S划分为2个子集S1和S2 ，基于平衡子问题的思想，用S中各点坐标的中位数来作分割点。
  递归地在S1和S2上找出其最接近点对{p1,p2}和{q1,q2}，并设d=min{|p1-p2|,|q1-q2|}，S中的最接近点对或者是{p1,p2}，或者是{q1,q2}，或者是某个{p3,q3}，其中p3∈S1且q3∈S2。
  能否在线性时间内找到p3,q3？

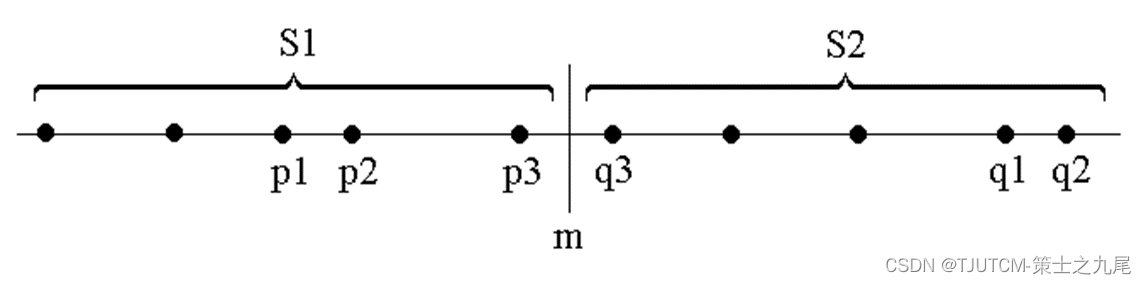
  如果S的最接近点对是{p3,q3}，即|p3-q3|<d，则p3和q3两者与m的距离不超过d，即p3∈(m-d,m]，q3∈(m,m+d]。
  由于在S1中，每个长度为d的半闭区间至多包含一个点（否则必有两点距离小于d），并且m是S1和S2的分割点，因此(m-d,m]中至多包含S中的一个点。由图可以看出，如果(m-d,m]中有S中的点，则此点就是S1中最大点。
  因此，我们用线性时间就能找到区间(m-d,m]和(m,m+d]中所有点，即p3和q3。从而我们用线性时间就可以将S1的解和S2的解合并成为S的解。

  下面来考虑二维的情形。
  选取一垂直线l:x=m来作为分割直线。其中m为S中各点x坐标的中位数。由此将S分割为S1和S2。
  递归地在S1和S2上找出其最小距离d1和d2，并设d=min{d1,d2}，S中的最接近点对或者是d，或者是某个{p,q}，其中p∈P1且q∈P2。
  能否在线性时间内找到p,q？

  能否在线性时间内找到p3,q3？
  考虑P1中任意一点p，它若与P2中的点q构成最接近点对的候选者，则必有distance(p，q)＜d。满足这个条件的P2中的点一定落在一个d×2d的矩形R中
  由d的意义可知，P2中任何2个S中的点的距离都不小于d。由此可以推出矩形R中最多只有6个S中的点。
  因此，在分治法的合并步骤中最多只需要检查6×n/2=3n个候选者


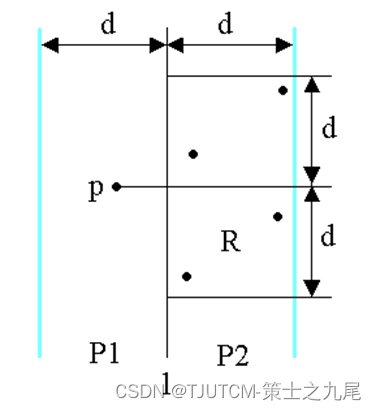
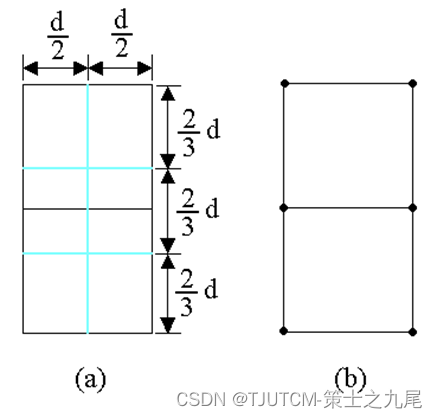
  证明:将矩形R的长为2d的边3等分，将它的长为d的边2等分，由此导出6个(d/2)×(2d/3)的矩形。若矩形R中有多于6个S中的点，则由鸽舍原理易知至少有一个(d/2)×(2d/3)的小矩形中有2个以上S中的点。设u，v是位于同一小矩形中的2个点，则

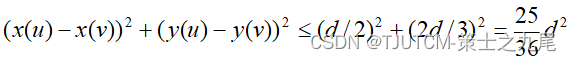
distance(u,v)<d。这与d的意义相矛盾。

  为了确切地知道要检查哪6个点，可以将p和P2中所有S2的点投影到垂直线l上。由于能与p点一起构成最接近点对候选者的S2中点一定在矩形R中，所以它们在直线l上的投影点距p在l上投影点的距离小于d。由上面的分析可知，这种投影点最多只有6个。
  因此，若将P1和P2中所有S中点按其y坐标排好序，则对P1中所有点，对排好序的点列作一次扫描，就可以找出所有最接近点对的候选者。对P1中每一点最多只要检查P2中排好序的相继6个点。

double cpair2(S)
{
      n=|S|;
      if (n < 2) return ;
1、m=S中各点x间坐标的中位数;
      构造S1和S2；
      //S1={p∈S|x(p)<=m}, 
     S2={p∈S|x(p)>m}
2、d1=cpair2(S1);
      d2=cpair2(S2);
3、dm=min(d1,d2);
4、设P1是S1中距垂直分割线l的距离在dm之内的所有点组成的集合；
      P2是S2中距分割线l的距离在dm之内所有点组成的集合；
      将P1和P2中点依其y坐标值排序；
      并设X和Y是相应的已排好序的点列；
5、通过扫描X以及对于X中每个点检查Y中与其距离在dm之内的所有点(最多6个)可以完成合并；
      当X中的扫描指针逐次向上移动时，Y中的扫描指针可在宽为2dm的区间内移动；
      设dl是按这种扫描方式找到的点对间的最小距离；
6、d=min(dm,dl);
      return d;
}

---

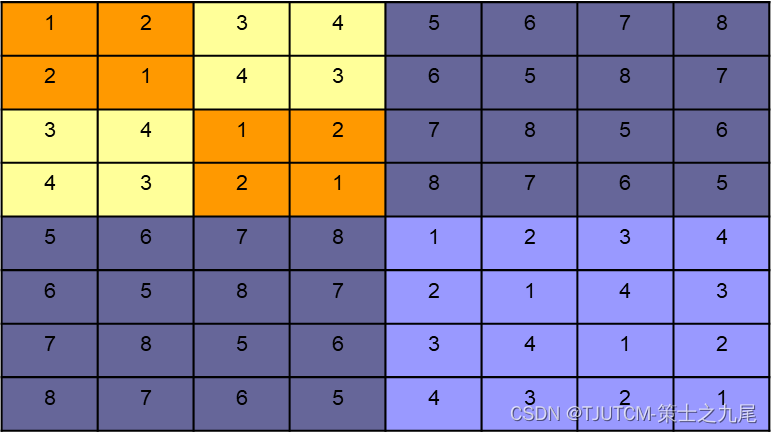
10、循环赛日程表

  设计一个满足以下要求的比赛日程表：
  (1)每个选手必须与其他n-1个选手各赛一次；
  (2)每个选手一天只能赛一次；
  (3)循环赛一共进行n-1天。
  按分治策略，将所有的选手分为两半，n个选手的比赛日程表就可以通过为n/2个选手设计的比赛日程表来决定。递归地用对选手进行分割，直到只剩下2个选手时，比赛日程表的制定就变得很简单。这时只要让这2个选手进行比赛就可以了。