📚实验目的

• 通过实际编程掌握仿射密码的破译，实现对仿射密码算法以及破解方式的深入理解，考虑在破解过程中密钥长度和密码算法本身的设计对安全性的影响，并思考如何设计更安全的加密算法。具体内容：
• 1）使用暴力破解的方式对仿射加密进行破解，还原明文；
• 2）使用词频统计的方式对仿射加密进行破解，还原明文。
• 3）在同一运行环境下，对比两种破解方式所需的时间。

📚关于仿射加密

🔥使用暴力破解的方式对仿射加密进行破解，还原明文

1. 定义一个空字符串ans，用于存储解密后的明文。
2. 使用三个嵌套的循环遍历alpha_inverse列表、0到25的beta列表和密文中的每个字符。

   1. 如果字符是空格，则将空格添加到结果字符串ans中。

   2. 如果字符是小写英文字母，则计算字符的偏移量cur（密文字符的ASCII码 - 'a’的ASCII码 - beta）。根据公式解密字符并将解密后的字符添加到结果字符串ans中。公式：chr(((cur * alpha_inverse[j]) % 26) + ord('a'))

   3. 如果字符是大写英文字母，同样计算字符的偏移量cur，并根据公式解密字符并将解密后的字符添加到结果字符串ans中。公式：chr(((cur * alpha_inverse[j]) % 26) + ord('A'))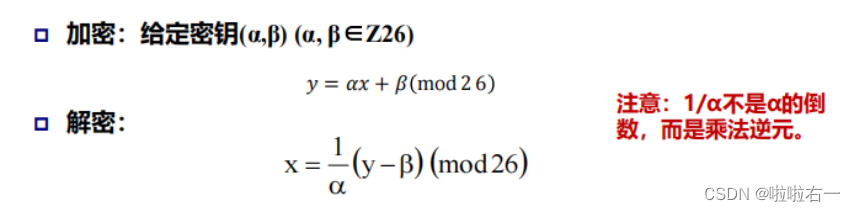

   4. 如果字符不是字母，直接将字符添加到结果字符串ans中。

3. 打印出解密结果。
4. 清空结果字符串ans，为下一组合结果做准备。

alpha = [1, 3, 5, 7, 9, 11, 15, 17, 19, 21, 23, 25]
alpha_inverse = [1, 9, 21, 15, 3, 19, 7, 23, 11, 5, 17, 25]

---

# 暴力破解仿射加密
def baoli(mi):
    ans = ""
    # 遍历alpha_inverse列表
    for j in range(len(alpha_inverse)):
        # 遍历0到25的beta列表
        for k in range(26):
            # 遍历密文中的每个字符
            for i in range(len(mi)):
                # 如果字符为空格，将空格添加到结果字符串
                if mi[i] == ' ':
                    ans += ' '
                # 如果字符是小写英文字母
                elif mi[i].islower():
                    # 计算字符的偏移量
                    cur = ord(mi[i]) - ord('a') - k
                    # 解密并将解密后的字符添加到结果字符串
                    if cur >= 0:
                        ans += chr(((cur * alpha_inverse[j]) % 26) + ord('a'))
                    else:
                        ans += chr(((26 + cur) * alpha_inverse[j]) % 26 + ord('a'))
                # 如果字符是大写英文字母
                elif mi[i].isupper():
                    # 计算字符的偏移量
                    cur = ord(mi[i]) - ord('A') - k
                    # 解密并将解密后的字符添加到结果字符串
                    if cur >= 0:
                        ans += chr(((cur * alpha_inverse[j]) % 26) + ord('A'))
                    else:
                        ans += chr(((26 + cur) * alpha_inverse[j]) % 26 + ord('A'))
                # 如果字符不是字母,将字符直接添加到结果字符串
                else:
                    ans += mi[i]
            print("α逆=", alpha_inverse[j], ",β=", k, "时的明文：", ans)
            # 清空结果字符串,用于下一组合结果存储
            ans = ""

---

密文：Ptfxgj Jnno-afv wn Htzaixojv Tjtxg

🔥使用词频统计的方式对仿射加密进行破解，还原明文

1. 定义一个空字符串ans，用于存储解密后的明文。

2. 创建一个列表b，用于记录每个字母在密文中出现的次数，初始值都为0。

   1. 遍历密文中的每个字符，如果字符是小写英文字母，则将对应位置的计数器值加1；如果字符是大写英文字母，则同样将对应位置的计数器值加1。
   2. 找到出现次数最多的字母maxchar和其对应的次数time_max，以及出现次数第二多的字母secondchar和其对应的次数time_secmax。
   3. 将最多字母maxchar的计数器值置为0，排除对找到次常出现字母的干扰。
   4. 将出现频率最多和次多的字母分别映射为e和t
      

3. 遍历alpha_inverse列表和0到25的beta列表，找到满足条件的alpha_inverse和beta。

   if (((alpha[j] * 4 + k) % 26) == (ord(maxchar) - ord('a'))) and (((alpha[j] * 19 + k) % 26) == (ord(secondchar) - ord('a')))
   

4. 再次遍历密文中的每个字符，根据解密的密钥alpha_inverse和beta进行解密操作，并将解密后的字符添加到结果字符串ans中。
5. 返回解密后的结果字符串ans。

---

# 使用词频统计方式破解仿射加密
def count(mi):
    ans = ""
    # 用于记录每个字母在密文中出现的次数的列表
    b = [0] * 26
    # 遍历密文中的每个字符统计出现次数
    for i in range(len(mi)):
        if mi[i].islower():
            b[ord(mi[i]) - ord('a')] += 1
        elif mi[i].isupper():
            b[ord(mi[i]) - ord('A')] += 1

    # 出现次数最多的字母
    maxchar = ''
    # 最大出现次数
    time_max = 0
    # 最大出现次数字母的索引
    index = 0
    # 遍历26个字母找最大出现次数的字母
    for i in range(26):
        if b[i] > time_max:
            maxchar = chr(i + ord('a'))
            time_max = b[i]
            index = i
    # 将最大出现次数字母的次数置为0，排除对找次常出现字母的干扰
    b[index] = 0

    # 找次常出现字母
    secondchar = ''
    time_secmax = 0
    for i in range(26):
        if b[i] > time_secmax:
            secondchar = chr(i + ord('a'))
            time_secmax = b[i]

    # 解密的密钥alpha_inverse
    key_alpha = 0
    # 解密的密钥beta
    beta = 0
    # 遍历alpha_inverse列表
    for j in range(len(alpha_inverse)):
        # 遍历0到25的beta列表
        for k in range(26):
            # 如果找到满足条件的alpha_inverse和beta
            if (((alpha[j] * 4 + k) % 26) == (ord(maxchar) - ord('a'))) and (((alpha[j] * 19 + k) % 26) == (ord(secondchar) - ord('a'))):
                # 更新解密的密钥alpha_inverse
                key_alpha = alpha_inverse[j]
                # 更新解密的密钥beta
                beta = k
                break

    # 遍历密文中的每个字符,解密
    for i in range(len(mi)):
        if mi[i] == ' ':
            ans += ' '
        elif mi[i].islower():
            cur = ord(mi[i]) - ord('a') - beta
            if cur >= 0:
                ans += chr(((cur * key_alpha) % 26) + ord('a'))
            else:
                ans += chr(((26 + cur) * key_alpha) % 26 + ord('a'))
        elif mi[i].isupper():
            cur = ord(mi[i]) - ord('A') - beta
            if cur >= 0:
                ans += chr(((cur * key_alpha) % 26) + ord('A'))
            else:
                ans += chr(((26 + cur) * key_alpha) % 26 + ord('A'))
        else:
            ans += mi[i]
    return ans

---

最高频对应e，次高频对应t

🔥在同一运行环境下，对比两种破解方式所需的时间

1. 暴力解法的时间复杂度较高，因为它需要尝试所有可能的alpha_inverse和beta的组合。对于每一组组合，还需要遍历整个密文进行解密操作。因此，当密文较长时，暴力解法的运行时间会显著增加。
2. 统计词频法相比暴力解法，由于利用了词频信息，它可能能够更快地找到出现频率最高的字母和次常出现的字母，从而确定解密的密钥。因此，统计词频法通常要比暴力解法快速一些，尤其是针对较长密文时。

📚分析体会

1. 仿射加密是一种基于数学运算的密码算法，它将明文中的每个字符通过一个线性变换映射到密文中的对应字符。该线性变换由两个参数alpha和beta决定。具体来说，给定一个字符x（大小写英文字母），则其在仿射加密中的加密运算为：加密(x) = (alpha * x + beta) mod 26，其中mod 26表示对26取模运算。解密则是加密的逆运算：解密(y) = alpha_inverse * (y - beta) mod 26，其中alpha_inverse表示alpha的逆元。
2. 暴力破解：该方法通过尝试所有可能的alpha_inverse和beta的组合来破解密文。它会遍历所有可能的参数组合，并将解密后的结果与已知的明文库进行匹配，从而找到正确的参数组合以解密密文。暴力破解的时间复杂度较高，尤其是对于较长的密文，所需的时间可能很长。
3. 统计词频法：该方法利用了密文中字母的词频信息来猜测解密的参数。首先，统计密文中每个字母的出现次数，找到出现频率最高的字母，以及次常出现的字母。然后利用这两个字母的位置关系及其对应的解密公式，可以得到解密的参数alpha_inverse和beta。通过这种方式，不需要穷举所有可能的参数组合，从而提高破解速度。