https://leetcode.cn/problems/ones-and-zeroes/description/
给你一个二进制字符串数组 strs 和两个整数 m 和 n 。
请你找出并返回 strs 的最大子集的长度,该子集中 最多 有 m 个 0 和 n 个 1 。
如果 x 的所有元素也是 y 的元素,集合 x 是集合 y 的 子集 。
示例 1:
输入:strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3
输出:4
解释:最多有 5 个 0 和 3 个 1 的最大子集是 {"10","0001","1","0"} ,因此答案是 4 。
其他满足题意但较小的子集包括 {"0001","1"} 和 {"10","1","0"} 。{"111001"} 不满足题意,因为它含 4 个 1 ,大于 n 的值 3 。
示例 2:
输入:strs = ["10", "0", "1"], m = 1, n = 1
输出:2
解释:最大的子集是 {"0", "1"} ,所以答案是 2 。
>>思考和分析
- x:统计字符串中0的个数总和
- y:统计字符串中1的个数总和
动规五部曲
1.确定dp数组(dp table)以及下标的含义
dp[i][j]:最多有 i个'0' 和 j个'1'的 strs的最大子集的大小为dp[i][j]
↓
dp[i][j]:i个'0' j个'1' 最大背dp[i][j]个 物品
↓
所求 dp[m][n]
2.确定递推公式
0-1背包的一维dp数组的递推公式:
dp[j] = max(dp[j],dp[j - weight[i]] + value[i]);
↓将一维度扩展为二维😚
dp[i][j] = max(dp[i][j],dp[i - x][j - y] + 1);
关键:对比以下,我们就可以得知字符串的 x 和 y相当于物品的重量(weight[i]),字符串本身的个数相当于物品的价值(value[i])
本质:这就是一个典型的01背包问题!!!只不过物品的重量有了两个维度而已(●'~'●)
3.初始化
dp[0][0],非0下标的也初始化为0(因为物品价值不会是负数,初始为0,保证递推的时候dp[i][j]不会被初始值覆盖)
4.确定遍历顺序
在0-1背包中一定是外层for循环遍历物品,内层for循环遍历背包容量且从后向前遍历!
本题中,物品就是strs中的字符串,背包容量就是题目描述中的m 和 n
5.举例推导dp数组
以输入:["10","0001","111001","1","0"],m = 3,n = 3为例
(1)dp数组初始化为如下图,i 和 j 分别表示背包容量的两个维度
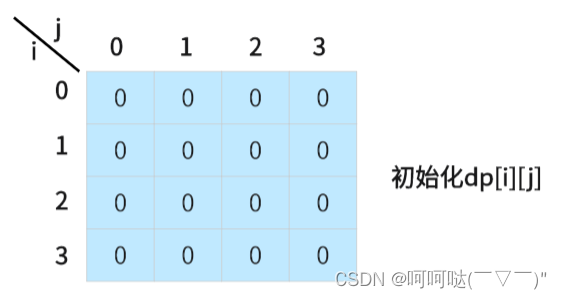
(2)遍历字符串数组,获取到"10",我们可以计算出x个"0" 和 y个"1"

然后更新dp数组,推导如下:
dp[3][3] = max(dp[3][3],dp[3-1][3-1] + 1)= max(0,dp[2][2] + 1) = 1
dp[3][2] = max(dp[3][2],dp[3-1][2-1] + 1)= max(0,dp[2][1] + 1) = 1
dp[3][1] = max(dp[3][1],dp[3-1][1-1] + 1)= max(0,dp[2][0] + 1) = 1
------------------------------------------------------------------
dp[2][3] = max(dp[2][3],dp[2-1][3-1] + 1)= max(0,dp[1][2] + 1) = 1
dp[2][2] = max(dp[2][2],dp[2-1][2-1] + 1)= max(0,dp[1][1] + 1) = 1
dp[2][1] = max(dp[2][1],dp[2-1][1-1] + 1)= max(0,dp[1][0] + 1) = 1
------------------------------------------------------------------
dp[1][3] = max(dp[1][3],dp[1-1][3-1] + 1)= max(0,dp[0][2] + 1) = 1
dp[1][2] = max(dp[1][2],dp[1-1][2-1] + 1)= max(0,dp[0][1] + 1) = 1
dp[1][1] = max(dp[1][1],dp[1-1][1-1] + 1)= max(0,dp[0][0] + 1) = 1(3)遍历字符串数组,获取到"0001",我们可以计算出x个"0" 和 y个"1"
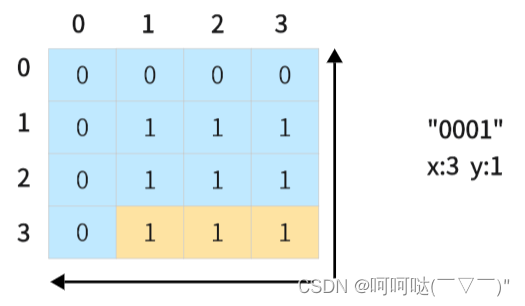
然后更新dp数组,推导如下:
dp[3][3] = max(dp[3][3],dp[3-3][3-1] + 1)= max(1,dp[0][2] + 1) = 1
dp[3][2] = max(dp[3][2],dp[3-3][2-1] + 1)= max(1,dp[0][1] + 1) = 1
dp[3][1] = max(dp[3][1],dp[3-3][1-1] + 1)= max(1,dp[0][0] + 1) = 1(4)遍历字符串数组,获取到"111001",我们可以计算出x个"0" 和 y个"1"
我们可以算出x = 2,y = 4,y = 4超出 j 的界限,所以无需要更新

(5)遍历字符串数组,获取到"1",我们可以计算出x个"0" 和 y个"1"

然后更新dp数组,推导如下:
dp[3][3] = max(dp[3][3],dp[3-0][3-1] + 1)= max(1,dp[3][2] + 1) = 2
dp[3][2] = max(dp[3][2],dp[3-0][2-1] + 1)= max(1,dp[3][1] + 1) = 2
dp[3][1] = max(dp[3][1],dp[3-0][1-1] + 1)= max(1,dp[3][0] + 1) = 1
------------------------------------------------------------------
dp[2][3] = max(dp[2][3],dp[2-0][3-1] + 1)= max(1,dp[2][2] + 1) = 2
dp[2][2] = max(dp[2][2],dp[2-0][2-1] + 1)= max(1,dp[2][1] + 1) = 2
dp[2][1] = max(dp[2][1],dp[2-0][1-1] + 1)= max(1,dp[2][0] + 1) = 1
------------------------------------------------------------------
dp[1][3] = max(dp[1][3],dp[1-0][3-1] + 1)= max(1,dp[1][2] + 1) = 2
dp[1][2] = max(dp[1][2],dp[1-0][2-1] + 1)= max(1,dp[1][1] + 1) = 2
dp[1][1] = max(dp[1][1],dp[1-0][1-1] + 1)= max(1,dp[1][0] + 1) = 1
------------------------------------------------------------------
dp[0][3] = max(dp[0][3],dp[0-0][3-1] + 1)= max(0,dp[0][2] + 1) = 1
dp[0][2] = max(dp[0][2],dp[0-0][2-1] + 1)= max(0,dp[0][1] + 1) = 1
dp[0][1] = max(dp[0][1],dp[0-0][1-1] + 1)= max(0,dp[0][0] + 1) = 1(6)遍历字符串数组,获取到"0",我们可以计算出x个"0" 和 y个"1"

然后更新dp数组,推导如下:
dp[3][3] = max(dp[3][3],dp[3-1][3-0] + 1)= max(2,dp[2][3] + 1) = 3
dp[3][2] = max(dp[3][2],dp[3-1][2-0] + 1)= max(2,dp[2][2] + 1) = 3
dp[3][1] = max(dp[3][1],dp[3-1][1-0] + 1)= max(1,dp[2][1] + 1) = 2
dp[3][0] = max(dp[3][0],dp[3-1][0-0] + 1)= max(0,dp[2][0] + 1) = 1
------------------------------------------------------------------
dp[2][3] = max(dp[2][3],dp[2-1][3-0] + 1)= max(2,dp[1][3] + 1) = 3
dp[2][2] = max(dp[2][2],dp[2-1][2-0] + 1)= max(2,dp[1][2] + 1) = 3
dp[2][1] = max(dp[2][1],dp[2-1][1-0] + 1)= max(1,dp[1][1] + 1) = 2
dp[2][0] = max(dp[2][1],dp[2-1][0-0] + 1)= max(0,dp[1][0] + 1) = 1
------------------------------------------------------------------
dp[1][3] = max(dp[1][3],dp[1-1][3-0] + 1)= max(2,dp[0][3] + 1) = 2
dp[1][2] = max(dp[1][2],dp[1-1][2-0] + 1)= max(2,dp[0][2] + 1) = 2
dp[1][1] = max(dp[1][1],dp[1-1][1-0] + 1)= max(1,dp[0][1] + 1) = 2
dp[1][0] = max(dp[1][1],dp[1-1][0-0] + 1)= max(0,dp[0][0] + 1) = 1(7)获取最终结果dp[m][n]

完整代码:
class Solution {
public:
int findMaxForm(vector<string>& strs, int m, int n) {
vector<vector<int>> dp(m + 1, vector<int> (n + 1, 0)); // 默认初始化0
for(string str:strs) {// 物品
int x=0,y=0;
for(char c:str) {
if(c == '0') x++;
else y++;
}
for(int i=m;i>=x;i--) { // 背包
for(int j=n;j>=y;j--) {
dp[i][j] = max(dp[i][j],dp[i-x][j-y] + 1);
}
}
}
return dp[m][n];
}
};来自代码随想录的课堂截图

参考和推荐文章、视频:
动态规划之背包问题,装满这个背包最多用多少个物品?| LeetCode:474.一和零_哔哩哔哩_bilibili 代码随想录 (programmercarl.com)