---

前言

在centos7的环境中，编译安装opencv，获得libopencv_java2413.so、opencv-2413.jar的库文件和jar包文件

---

一、问题来源

异常提示：java.lang.UnsatisfiedLinkError: no opencv_java2413 in java.library.path

二、编译安装

1.下载源码

代码如下（示例）：

wget https://github.com/opencv/opencv/archive/2.4.13.zip

2.安装基础环境

yum install unzip -y
yum install cmake -y
yum install python python-devel-y
yum install gcc gcc-c++ -y
yum groupinstall "Development Tools" -y

3.安装java环境

一定要先安装ant，再执行编译

yum install ant -y

4.编译安装

unzip 2.4.13.zip
cd opencv-2.4.13/
cmake CMakeLists.txt
make 
make install

cmake 输出的java环境信息

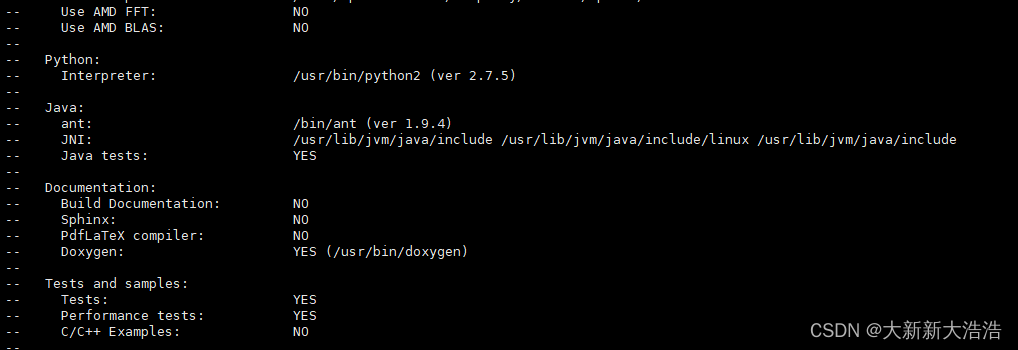
make输出的java相关信息

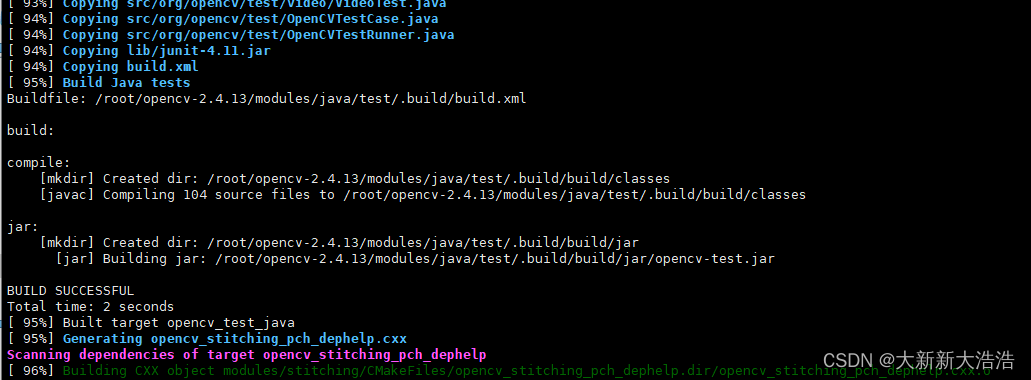
5.查询结果

find / -name 'opencv-2413.jar'
find / -name 'libopencv_java2413.so'

结果

/root/opencv-2.4.13/modules/java/test/.build/bin/opencv-2413.jar
/root/opencv-2.4.13/bin/opencv-2413.jar
/usr/local/share/OpenCV/java/opencv-2413.jar
/root/opencv-2.4.13/lib/libopencv_java2413.so
/usr/local/share/OpenCV/java/libopencv_java2413.so

---

总结

一定要安装ant之后再编译，否则不会出现java相关的编译后文件