动态规划
- 爬楼梯问题
- 解法1
- 第一步
- 第二步
- 第三步
- JAVA实现
- 解法2
- 问题建模
- 最优子结构
- 边界
- 状态转移公式
- 求解问题
- 递归JAVA实现
- 备忘录算法JAVA实现
- 解法三JAVA实现(斐波那契数列)
- 国王和金矿
- 一个错误的解法
- 排列组合解法
- JAVA实现
- 动态规划
爬楼梯问题
有一座高度是10级台阶的楼梯,从下往上走,每跨一步只能向上1级或者2级台阶。要求用程序来求出一共有多少种走法。
解法1
利用排列组合公式求解此题,穷举出所有的组合情况。。。。
第一步
- 台阶个数10阶
- 一次上1阶或2阶—>(求利用1和2组成10的所有排列数目)
- 一旦1的数目确定,2的数目也确定了
- 1上限100
- 2上限50
第二步
设置循环
int i ;//一次爬2阶楼梯的次数
int j ;//一次爬1阶楼梯的次数
for (i=0;i<51;i++){
j = 100-2*i;
}
第三步
计算每个循环中,组合数量是多少(就是说1和2的数目确定了,求不同顺序排列的数目)

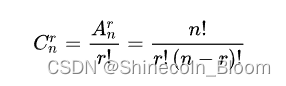
其中n是所有的1和2的数目,只要确定1或者2的排列,总的顺序就确定了。
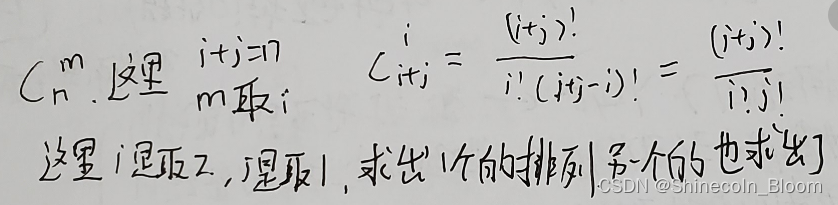
JAVA实现
//求阶乘方法
public static long factorialUsingForLoop(int n) {
long fact = 1;
for (int i = 2; i <= n; i++) {
fact = fact * i;
}
return fact;
}
/**
* 求n阶楼梯的所有爬法
* @param n 多少阶楼梯
* @return
*/
public static long sumclimbingStairs(int n){
int i ;//一次爬2阶楼梯的次数
int j ;//一次爬1阶楼梯的次数
long a ;
long b;
long c;
long sum=0;//累加每次排列的数目,计算总的数目
for (i=0;i<=(n/2);i++){
j = n-(2*i);
//这里注意总数目是i+j不是n........
a = factorialUsingForLoop(i+j);
b = factorialUsingForLoop(j);//这里是Cn1(计算的1的排列)
c = factorialUsingForLoop(i);
sum =sum+ a/(b*c);
}
return sum;
}
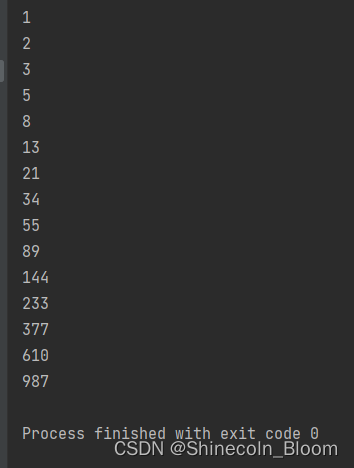
测试方法
public static void main(String[] args) {
System.out.println(sumclimbingStairs(1));
System.out.println(sumclimbingStairs(2));
System.out.println(sumclimbingStairs(3));
System.out.println(sumclimbingStairs(4));
System.out.println(sumclimbingStairs(5));
System.out.println(sumclimbingStairs(6));
System.out.println(sumclimbingStairs(7));
System.out.println(sumclimbingStairs(8));
System.out.println(sumclimbingStairs(9));
System.out.println(sumclimbingStairs(10));
System.out.println(sumclimbingStairs(11));
System.out.println(sumclimbingStairs(12));
System.out.println(sumclimbingStairs(13));
System.out.println(sumclimbingStairs(14));
System.out.println(sumclimbingStairs(15));
//System.out.println(factorialUsingForLoop(4));
}
参考
解法2
动态规划(Dynamic Programming)是一种分阶段求解决策问题的数学思想
大事化小,小事化了。。
把复杂的问题简化成规模较小的子问题,再从简单的子问题自底向上一步一步递推,最终得到复杂问题的最优解。
例子:爬10层楼梯 (假设爬前九层楼梯有X种方法,爬前八层楼梯有Y种方法)
- 完成前九层爬的楼梯数目+再爬一层
- 完成前八层爬的楼梯数目+再爬两层
- 爬10层楼梯一共的方法数目:X+Y种方法
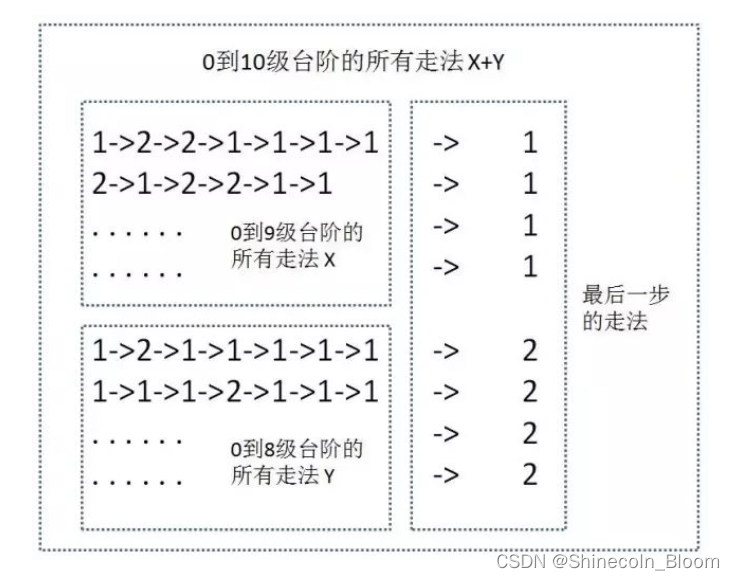
从0到10级台阶的走法数量=0到9级的走法数量+0到8级的走法数量。
把10级台阶的走法数量简写为F(10),此时F(10)=F(9)+F(8)
关键在于计算F(9)和F(8)
对于F(9)和F(8),我们有
F(9)=F(8)+F(7), F(8)=F(7)+F(6)
动态规划的思想:把一个复杂的问题分阶段进行简化,逐步简化成简单的问题。
直到递推到1级台阶和2级台阶
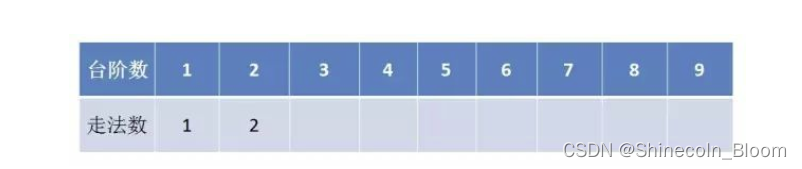
F(1) = 1
F(2) = 2
F(n) = F(n-1)+F(n-2)
动态规划的核心:最优子结构、边界、状态转移公式
问题建模
最优子结构
F(10)=F(9)+F(8)
所以F(9)和F(8)是F(10)的最优子结构
边界
F(1)和F(2)我们可以直接得到结果,
所以F(1)和F(2)是问题的边界
状态转移公式
F(n) = F(n-1)+F(n-2)是状态转移方程
求解问题
递归JAVA实现
边界对应递归出口,状态转移方程可以用递归实现
/**
* 求解爬楼梯
* @param n 楼梯的阶数
* @return
*/
public static int getClimbingWays(int n){
//递归出口
if(n<1){
return 0;
}
if(n==1){
return 1;
}
if(n==2){
return 2;
}
//递归调用
return getClimbingWays(n-1)+getClimbingWays(n-2);
}
测试方法
public static void main(String[] args) {
System.out.println(getClimbingWays(1));
System.out.println(getClimbingWays(2));
System.out.println(getClimbingWays(3));
System.out.println(getClimbingWays(4));
System.out.println(getClimbingWays(5));
System.out.println(getClimbingWays(6));
System.out.println(getClimbingWays(7));
System.out.println(getClimbingWays(8));
System.out.println(getClimbingWays(9));
System.out.println(getClimbingWays(10));
System.out.println(getClimbingWays(11));
System.out.println(getClimbingWays(12));
System.out.println(getClimbingWays(13));
System.out.println(getClimbingWays(14));
System.out.println(getClimbingWays(15));
}
就是把复杂的问题简化成规模较小的子问题,再从简单的子问题自底向上一步一步递推,最终得到复杂问题的最优解。
计算出F(N),就要先得到F(N-1)和F(N-2)的值。要计算F(N-1),就要先得到F(N-2)和F(N-3)的值…以此类推,可以归纳成下面的数图:
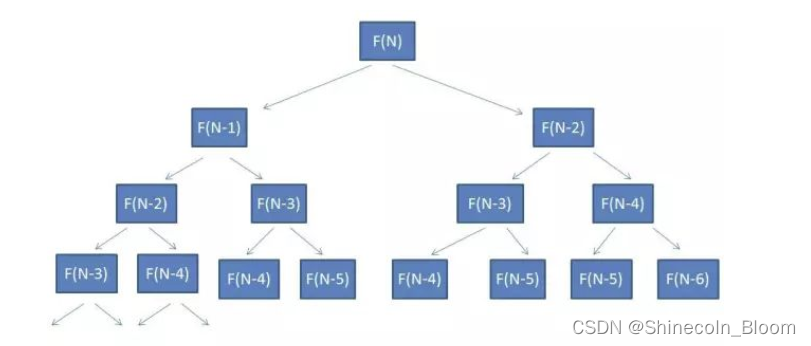
时间复杂度O(2n)
存在的问题,很多重复的计算。。。
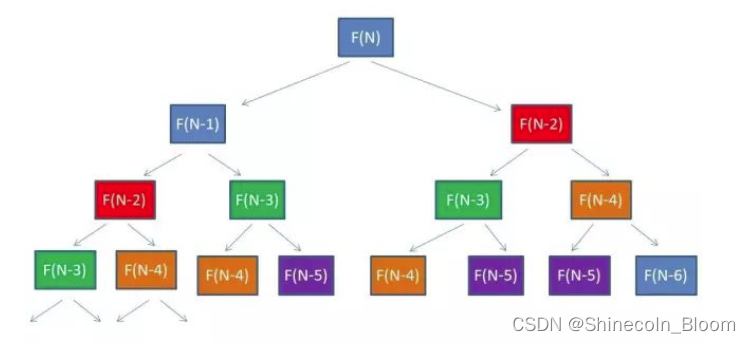
相同颜色是一样的传参,一样的计算。。
备忘录算法JAVA实现
针对以上问题,先创建一个哈希表,每次把不同参数的计算结果存入哈希。当遇到相同参数时,再从哈希表里取出,就不用重复计算了。
暂存计算结果
public static int getClimbingWays(int n, HashMap<Integer,Integer> map){
if(n<1){
return 0;
}
if(n==1){
return 1;
}
if(n==2){
return 2;
}
// //递归调用 (改写这个)
// return getClimbingWays(n-1)+getClimbingWays(n-2);
/**
* 集合map是一个备忘录。当每次需要计算F(N)的时候,
* 会首先从map中寻找匹配元素。如果map中存在,就直接返回结果,
* 如果map中不存在,就计算出结果,存入备忘录中。
*/
if(map.containsKey(n)){
return map.get(n);
}else {
int value= getClimbingWays(n-1,map)+getClimbingWays(n-2,map);
map.put(n,value);
return value;
}
}
测试方法:
public static void main(String[] args) {
HashMap<Integer,Integer> map = new HashMap<Integer,Integer>();
System.out.println(getClimbingWays(10,map));
}
集合map是一个备忘录。当每次需要计算F(N)的时候,会首先从map中寻找匹配元素。如果map中存在,就直接返回结果,如果map中不存在,就计算出结果,存入备忘录中。
时间复杂度:O(N),算过一次后直接取值
空间复杂度:O(N),因为空间存了n个值
if(map.containsKey(n)){
System.out.println("直接取值:f("+n+")");
return map.get(n);
}else {
int value= getClimbingWays(n-1,map)+getClimbingWays(n-2,map);
map.put(n,value);
return value;
}
解法三JAVA实现(斐波那契数列)
优化空间复杂度:自底向下,用迭代的方式推导出结果。
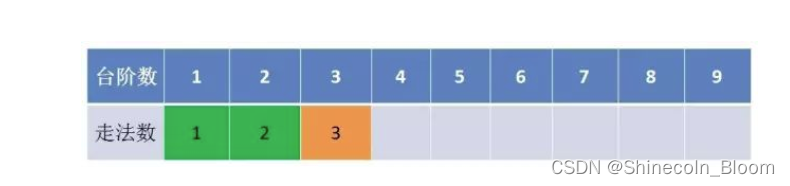

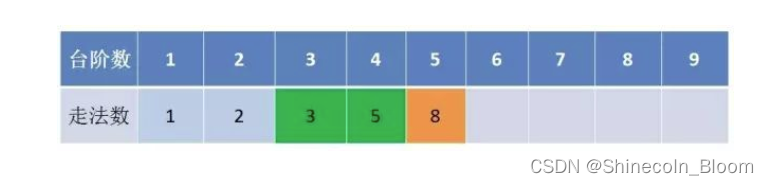
一次迭代过程中,只要保留之前的两个状态,就可以推导出新的状态。而不需要像备忘录算法那样保留全部的子状态。
优化空间复杂度
起其实这就是一个斐波那契数列
/**
* 爬楼梯
* @param n 楼梯数目
* @return
*/
public static int getClimbingWays(int n){
if(n<1){
return 0;
}
if(n==1){
return 1;
}
if(n==2){
return 2;
}
int a = 1;
int b = 2;
int temp = 0;
//自底向上---斐波那契数列
for (int i=3;i<=n;i++){
temp = a+b;
a = b;
b = temp;
}
return temp;
}
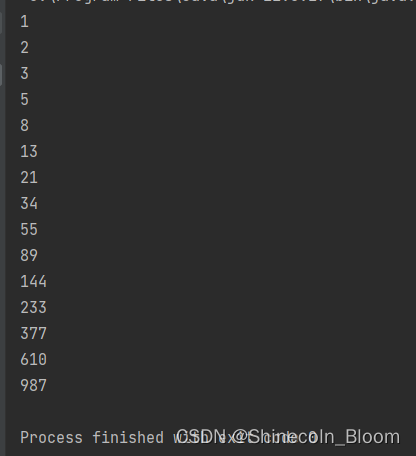
测试方法:
public static void main(String[] args) {
for (int i =1;i<16;i++){
System.out.println(getClimbingWays(i));
}
}
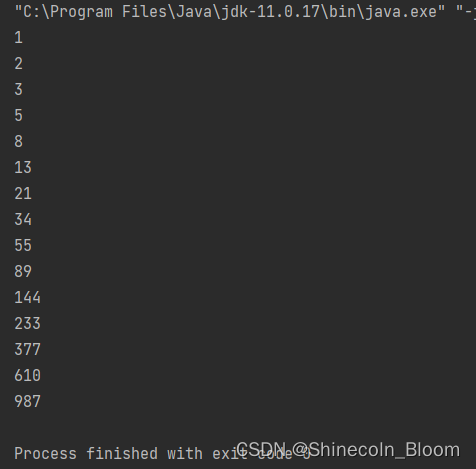
时间复杂度:O(n)
空间复杂度O(1)
迭代过程中只需保留两个临时变量a和b,分别代表了上一次和上上次迭代的结果。 为了便于理解,我引入了temp变量。temp代表了当前迭代的结果值
国王和金矿
很久很久以前,有一位国王拥有5座金矿,每座金矿的黄金储量不同,需要参与挖掘的工人人数也不同。例如有的金矿储量是500kg黄金,需要5个工人来挖掘;有的金矿储量是200kg黄金,需要3个工人来挖掘……如果参与挖矿的工人的总数是10。每座金矿要么全挖,要么不挖,不能派出一半人挖取一半的金矿。要求用程序求出,要想得到尽可能多的黄金,应该选择挖取哪几座金矿
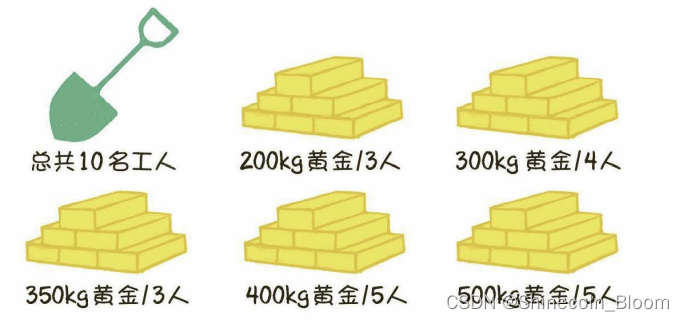
这是一个典型的动态规划题目,和著名的“背包问题”类似。
动态规划,就是把复杂的问题简化成规模较小的子问题,再从简单的子问题自底向上一步一步递推,最终得到复杂问题的最优解。
一个错误的解法
使用贪心算法
按照金矿的性价比从高到低进行排序,优先选择性价比最高的金矿来挖掘,然后是性价比第2的……

总工人10,挖掘了第一名和第二名的金矿后,剩下的2人就没法挖掘其他金矿了。
总收益:350+500=850.
局部情况下是最优解,但是在整体上却未必是最优的。
如果我放弃性价比最高的350kg黄金/3人的金矿,选择500kg黄金/5人和400kg黄金/5人的金矿,加起来收益是900kg。
排列组合解法
每一座金矿都有挖与不挖两种选择,如果有N座金矿,排列组合起来就有2N种选择。对所有可能性做遍历,排除那些使用工人数超过10的选择,在剩下的选择里找出获得金币数最多的选择。