- 本文只介绍哈密顿系统的辛算法的显式结构
- 不给出具体的推导过程
自洽可分的哈密顿系统的辛算法
- 一阶显式辛结构
- 二阶显式辛结构
- 四阶显式辛结构
- 全代码
import matplotlib.pyplot as plt
import numpy as np
from scipy.optimize import fsolve
##SymplecticHamilton
##self-consistent
##separable
class symhamcssolver():
def __init__(self, Up, Vq,
q0=np.array([0]),
p0=np.array([1]),
T_start=0, T_end=20, tau=0.01):
self.Up = Up
self.Vq = Vq
self.tau = tau
self.T = np.arange(T_start, T_end, self.tau)
self.size = len(self.T)
self.q = np.zeros((len(self.T), len(q0)))
self.q[0, :] = q0
self.p = np.zeros((len(self.T), len(p0)))
self.p[0, :] = p0
self.tol = 1e-6
def __str__(self):
return f"Symplectic algrithm of self-consistent and separable Hamilton system"
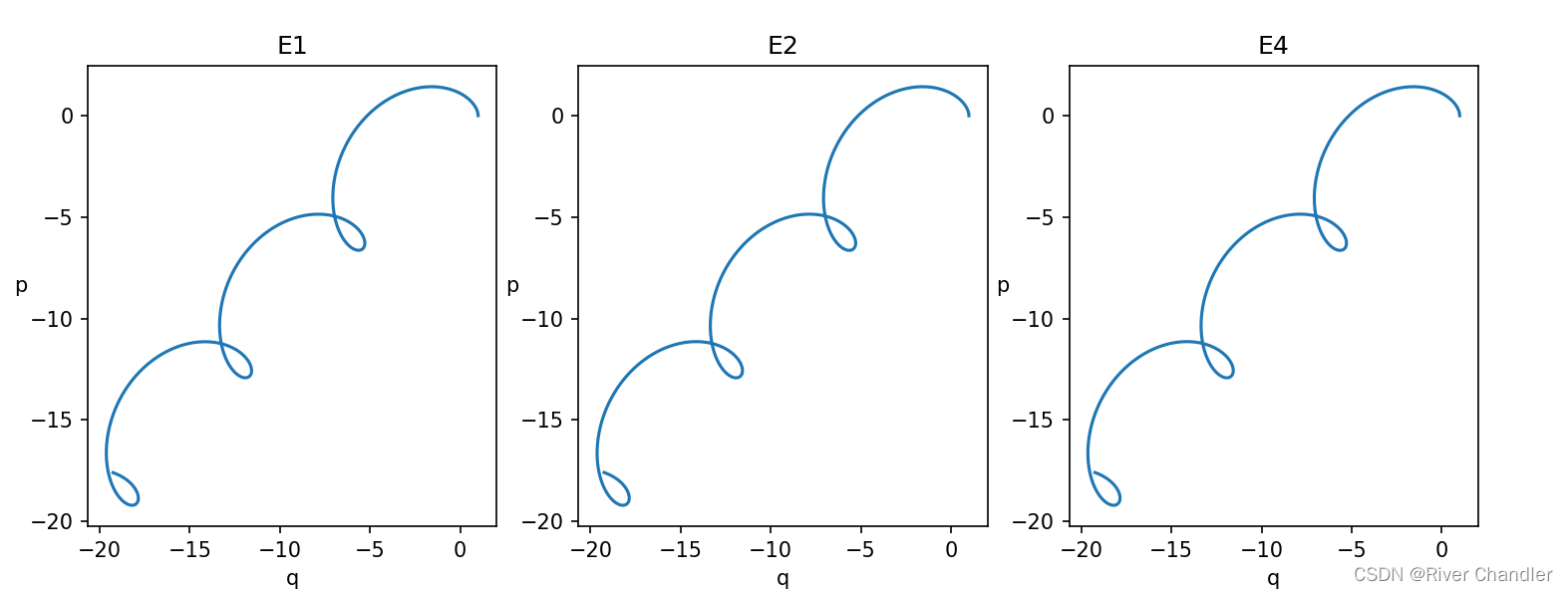
def E1(self,):
for i in range(1, self.size):
self.q[i, :] = self.q[i-1, :] + self.tau * self.Up(self.p[i-1, :])
self.p[i, :] = self.p[i-1, :] - self.tau * self.Vq(self.q[i, :])
return self.p, self.q
def E2(self,):
for i in range(1, self.size):
x = self.q[i-1, :]
y = self.p[i-1, :] - self.tau/2 * self.Vq(x)
self.q[i, :] = x + self.tau * self.Up(y)
self.p[i, :] = y - self.tau/2 * self.Vq(self.q[i, :])
return self.p, self.q
def E4(self,):
alpha = 1/(2-2**(1/3))
beta = 1 - 2 * alpha
c = np.zeros(5)
d = np.zeros(5)
c[2] = alpha
c[4] = alpha
c[3] = beta
d[1] = alpha/2
d[4] = alpha/2
d[2] = (alpha + beta)/2
d[3] = (alpha + beta)/2
for i in range(1, self.size):
x1 = self.q[i-1, :] + c[1] * self.tau * self.Up(self.p[i-1, :])
y1 = self.p[i-1, :] - d[1] * self.tau * self.Vq(x1)
x2 = x1 + c[2] * self.tau * self.Up(y1)
y2 = y1 - d[2] * self.tau * self.Vq(x2)
x3 = x2 + c[3] * self.tau * self.Up(y2)
y3 = y2 - d[3] * self.tau * self.Vq(x3)
self.q[i, :] = x3 + c[4] * self.tau * self.Up(y3)
self.p[i, :] = y3 - d[4] * self.tau * self.Vq(self.q[i, :])
return self.p, self.q
## H = p^2/2m + k/2q^2
m = 1
k = 1
Up = lambda p:p[:]/m
Vq = lambda q:k*q[:]
c = symhamcssolver(Up, Vq)
fig = plt.figure(figsize=(12, 4))
ax1 = fig.add_subplot(1,3,1)
ax2 = fig.add_subplot(1,3,2)
ax3 = fig.add_subplot(1,3,3)
p, q = c.E1()
ax1.plot(p, q)
ax1.set_title("E1")
ax1.set_xlabel("q")
ax1.set_ylabel("p", rotation=0)
p, q = c.E2()
ax2.plot(p, q)
ax2.set_title("E2")
ax2.set_xlabel("q")
ax2.set_ylabel("p", rotation=0)
p, q = c.E4()
ax3.plot(p, q)
ax3.set_title("E4")
ax3.set_xlabel("q")
ax3.set_ylabel("p", rotation=0)
plt.pause(0.01)
- 解示意图
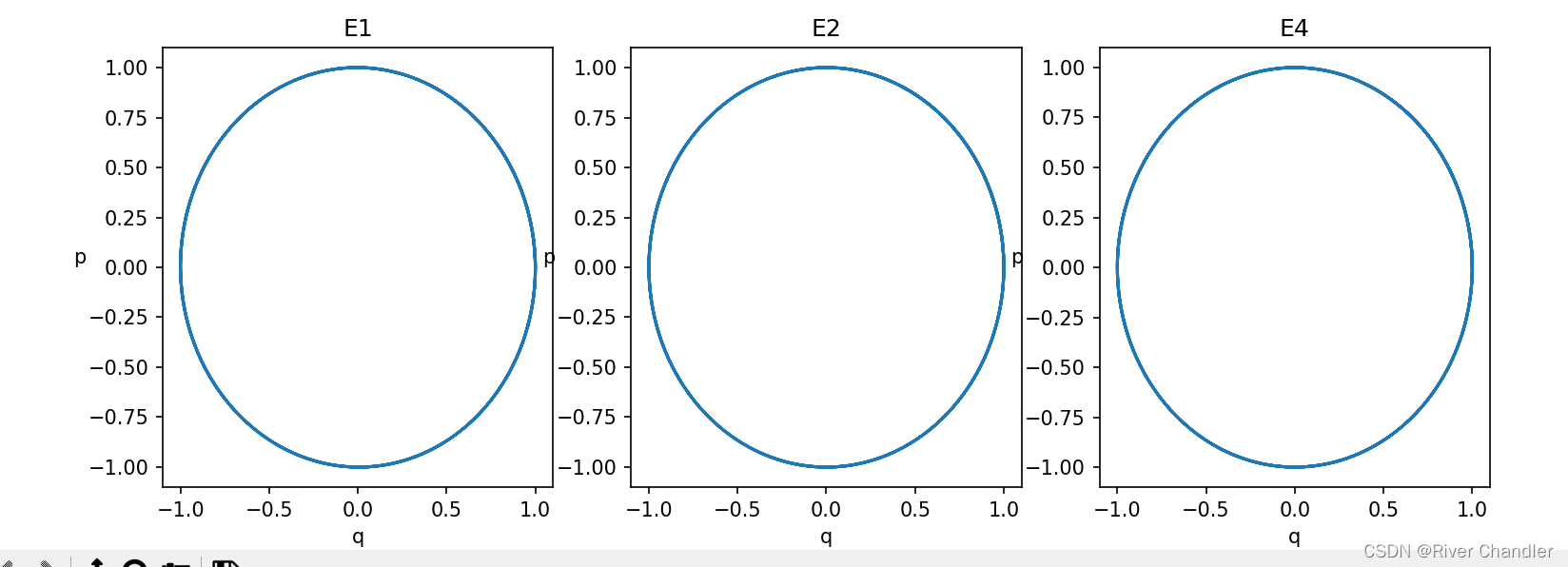
含时可分哈密顿系统
import matplotlib.pyplot as plt
import numpy as np
from scipy.optimize import fsolve
##SymplecticHamilton
##self-inconsistent
##separable
##
## \frac{dq}{dt} = U_p(p, t)
## \frac{dp}{dt} = -V_q(q, t)
##
class symhamicssolver():
def __init__(self, Up, Vq,
q0=np.array([0]),
p0=np.array([1]),
T_start=0, T_end=20, tau=0.01):
self.Up = Up
self.Vq = Vq
self.tau = tau
self.T = np.arange(T_start, T_end, self.tau)
self.size = len(self.T)
self.q = np.zeros((len(self.T), len(q0)))
self.q[0, :] = q0
self.p = np.zeros((len(self.T), len(p0)))
self.p[0, :] = p0
self.tol = 1e-6
def __str__(self):
return f"Symplectic algrithm of self-inconsistent and separable Hamilton system"
def E1(self,):
for i in range(1, self.size):
self.q[i, :] = self.q[i-1, :] + self.tau * self.Up(self.p[i-1, :], self.T[i-1])
self.p[i, :] = self.p[i-1, :] - self.tau * self.Vq(self.q[i, :] , self.T[i])
return self.p, self.q
def E2(self,):
for i in range(1, self.size):
x = self.q[i-1, :]
y = self.p[i-1, :] - self.tau/2 * self.Vq(x, self.T[i-1])
self.q[i, :] = x + self.tau * self.Up(y, self.T[i-1]+self.tau/2)
self.p[i, :] = y - self.tau/2 * self.Vq(self.q[i, :], self.T[i])
return self.p, self.q
def E4(self,):
alpha = 1/(2-2**(1/3))
beta = 1 - 2 * alpha
c = np.zeros(5)
d = np.zeros(5)
c[2] = alpha
c[4] = alpha
c[3] = beta
d[1] = alpha/2
d[4] = alpha/2
d[2] = (alpha + beta)/2
d[3] = (alpha + beta)/2
for i in range(1, self.size):
x1 = self.q[i-1, :] + c[1] * self.tau * self.Up(self.p[i-1, :], self.T[i])
zeta1 = self.T[i-1] + c[1] * self.tau
y1 = self.p[i-1, :] - d[1] * self.tau * self.Vq(x1, zeta1)
eta1 = self.T[i-1] + d[1] * self.tau
x2 = x1 + c[2] * self.tau * self.Up(y1, eta1)
zeta2 = zeta1 + c[2] * self.tau
y2 = y1 - d[2] * self.tau * self.Vq(x2, zeta2)
eta2 = eta1 + d[2] * self.tau
x3 = x2 + c[3] * self.tau * self.Up(y2, eta2)
zeta3 = zeta2 + c[3] * self.tau
y3 = y2 - d[3] * self.tau * self.Vq(x3, zeta3)
eta3 = eta2 + d[3] * self.tau
self.q[i, :] = x3 + c[4] * self.tau * self.Up(y3, eta3)
self.p[i, :] = y3 - d[4] * self.tau * self.Vq(self.q[i, :], self.T[i])
return self.p, self.q
## H = p^2/2m + k/2q^2
m = 1
k = 1
Up = lambda p, t:p[:]/m + t
Vq = lambda q, t:k*q[:] + t
c = symhamicssolver(Up, Vq)
fig = plt.figure(figsize=(12, 4))
ax1 = fig.add_subplot(1,3,1)
ax2 = fig.add_subplot(1,3,2)
ax3 = fig.add_subplot(1,3,3)
p, q = c.E1()
ax1.plot(p, q)
ax1.set_title("E1")
ax1.set_xlabel("q")
ax1.set_ylabel("p", rotation=0)
p, q = c.E2()
ax2.plot(p, q)
ax2.set_title("E2")
ax2.set_xlabel("q")
ax2.set_ylabel("p", rotation=0)
p, q = c.E4()
ax3.plot(p, q)
ax3.set_title("E4")
ax3.set_xlabel("q")
ax3.set_ylabel("p", rotation=0)
plt.pause(0.01)