文章目录
- 浮点数如何用二进制表示
- IEEE 浮点数标准
- IEEE 浮点数实现
- IEEE 浮点数在内存里
- E = exp - bias 计算指数
- M = 1.xxx 尾数计算
- 举例:对一个浮点数进行转换
- 一些关于浮点数的计算等等
浮点数如何用二进制表示
计算机内部的浮点数不是这样存在内存里的(至少C语言不是)但我们可以这样使用二进制来表示浮点数:
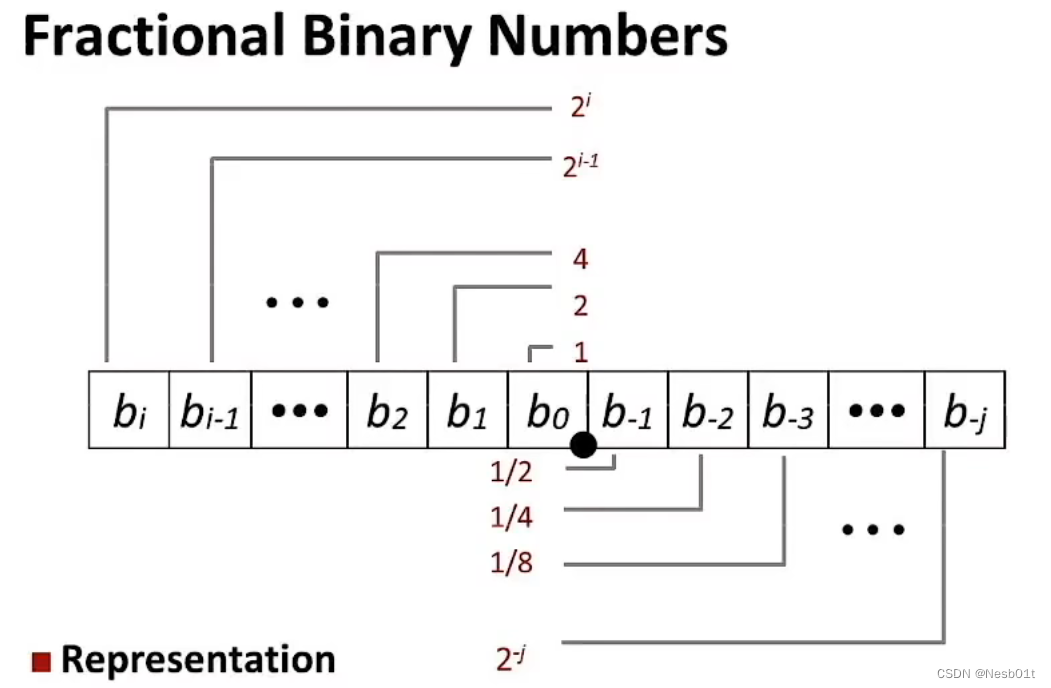
这样的表示方法有很大的局限,我们只能方便地表示 1/2,1/4 这样的数,如果要表示 1/3 之类的数字,那么只能是近似值

IEEE 浮点数标准
在1985以前,每一种计算机都可能有他自己的实现浮点数的方法,直到1985年计算机协会发布了 IEEE 754 标准,使得计算机厂商采用了一致的标准来支持浮点数

IEEE 浮点数实现
它使用一种类似科学计数法的方法来表示数字
其中:
- S 是符号位(0 或 1,用来设置是正还是负)
- M 是尾数(是一个在 1 ~ 2 之间的数字)
- 然后乘以 2 的 E 次幂(E 会以二进制幂形式用来扩大或减小 M 尾数,无论是32bits还是64bits)
所有浮点数都必须用这种方式来实现

IEEE 浮点数在内存里
32 bits 计算机中的 float:
- 1 位的 s 用来表示符号
- 8 位的 exp 指数,用来表示一种类似科学计数法的位数
- 23 位的 frac 尾数,也就是科学技术法的前半部分数值

E = exp - bias 计算指数
exp = 000…0 和 exp = 111…1 都是特殊的值,我们稍后讨论
指数 E 的值被解释为:以 偏置 biased 形式表示
所以 E 的实际值是 exp - bias
简单来说,exp 就是那个 7 位的值,把 exp 减去一个 bias 偏置值,就得到了 E 值!
对于 32 bits 的 float 浮点数来说,bias = 127,8 bits 的最高位权重是 128,128 - 1 = 127 就是 bias 了
那么 64 bits 呢?64 bits 的 exp 有 11 位,那么 11 bits 的最高权重就是 1024,1024 - 1 = 1023 就是 bias
我们此时得到了 bias = 127,接下来计算 exp 值
exp 值只需要把 除了第一位 以外 剩下的 7 位 当做二进制数字来计算就好了(这其实也是正负数补码的计算方式!)
这样做的好处是,如果要比较2个浮点数,刨去第一位以后就可以直接进行位运算比较!十分方便
- 最大的值就是 011111…1
- 最小的值就是 10000…0
M = 1.xxx 尾数计算
最小的尾数是 0000…0,此时 M = 1.0
最大的尾数是 1111…1,此时 M 超级接近 2.0
尾数就是 1.xxx 后面的 xxx,你把一堆 0 加起来当然是 0
你把一堆 1 加起来,那就是 1/2 + 1/4 + 1/8 … 最后当然是非常接近 1 的一个数
举例:对一个浮点数进行转换
多说无益,我们来举个例子,令 float F = 15213.0
经过二进制 表示,得到 15213(10进制的)= 11101101101101(二进制的)
使用科学计数法表示,得到 1.1101101101101 乘以 2的13次方
这样我们就得到了尾数 frac 和 M 的值:
- M = (去掉1.) 1101101101101
- frac = 11011011011010000000000
同时我们也得到了:
- E = 13(因为指数是13)
- Bias = 127(32 bits 的 float 就是127)
- Exp = 140(10001100,因为 Exp - Bias = 13,所以 Exp = 140)
这就是结果了,我们成功把 15213 这个十进制数,存到内存这个二进制结构里了~

一些关于浮点数的计算等等
后续关于浮点数在计算机里应用的细节内容可能会补上,暂时跳过,请看原视频~