系列文章目录

第一章 Python 机器学习入门之线性回归

前言

最近在上机器学习的课程，第一次实验是做线性回归，那神马是线性回归呢？

一、线性回归

1.线性回归是什么

根据百科给出的定义是这样子的，线性回归（Linear Regression）是利用称为线性回归方程的最小平方函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析




对于一个菜鸡来说有些深奥，先将这个概念拆开来看，回归是什么？

简单来说就是衡量多个自变量X对因变量Y的影响程度，同时预测因变量Y未来的发展趋势，举个简单的例子，在打王者的时候决定你击杀对手的因素很多，比如装备，技术，经济等等，在一定情况下，甚至可以直接通过经济的高低来判断你是否可以击杀对手，这也可以理解为一个相对简单的回归

那线性又是指什么呢?

线性通常是指变量之间保持等比例的关系，简单来说，你是一位大房东，你出租的房间越多，你每月获得的租金就越多，出租房间和租金之间就是一个等比例的关系；当然，这是一种假设。


最后就是线性回归了，就是要找出一条直线能直观地反映出自变量X和因变量Y之间的关系的过程

2.线性回归的分类

对于线性回归的分类，就是根据自变量X的数量来划分
当自变量X只有一个时，我们称之为一元线性回归
当自变量X超过一个时，我们称之为多元线性回归

二、实现线性回归

我们用一个例子来简单实现一下一元线性回归，假设你是一家奶茶店的老板，你目前有开设奶茶店的城市人口数据和利润，你想知道它们之间是否存在某种关系，来决定接下来开店的位置

1.步骤

1. 根据预测目标，确定自变量和因变量（自变量是人口，因变量是利润）
2. 绘制散点图，选择回归模型（将相关数据可视化并选择合适的模型）
3. 估计模型参数，建立回归模型（最小二乘法）
4. 对回归模型进行检验
5. 利用回归模型进行预测（找到接下来开店的城市）

2.代价函数

首先我们实现第一二步，将相关数据可视化展示出来，我们的回归模型就是线性回归模型；

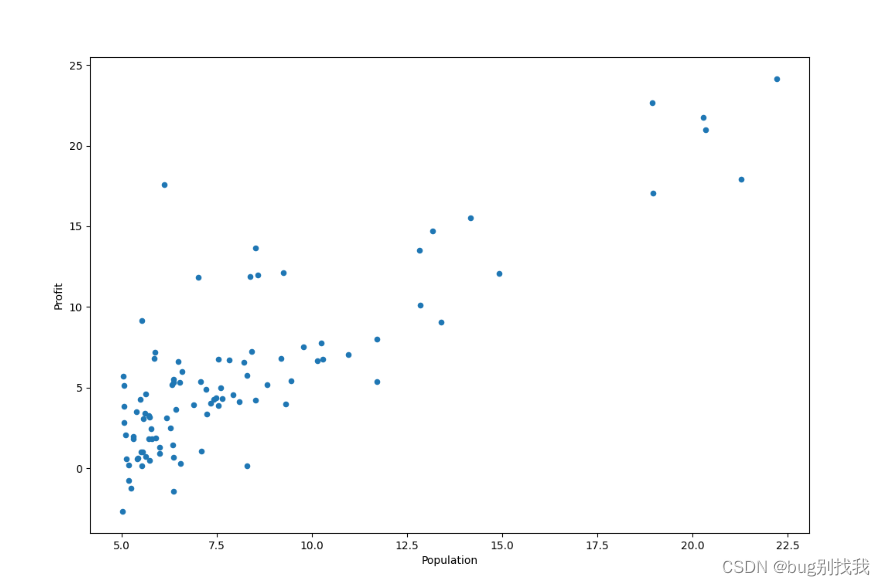
从图中我们可以看到真实情况往往是非常复杂的，而线性回归模型的任务就是找出一条能准确反映自变量X和因变量Y的直线，所以这当中肯定会出现误差，那让误差越小，我们的模型预测起来就更准确，那如何计算误差呢，就得使用代价函数了；

我们使用的是平方误差代价函数来计算最小代价，实现代码如下

# 最小化代价函数，X为训练数据，y是目标数据,theta是模型参数，即相关系数
def computeCost(X, y, theta):
    inner = np.power(((X * theta.T) - y), 2)
    return np.sum(inner) / (2 * len(X))

3.梯度下降

我们现在有了最小化代价函数，就可以通过它来找到最优的模型参数了；因此在前人的基础上我们采用梯度下降函数来寻找最小化的代价函数和模型参数值

# 梯度下降函数，X为训练数据，y是目标数据,theta是模型参数,alpha学习率,iters循环次数
def gradientDescent(X, y, theta, alpha, iters):
    temp = np.matrix(np.zeros(theta.shape))
    parameters = int(theta.ravel().shape[1])
    cost = np.zeros(iters)
    for i in range(iters):
        error = (X * theta.T) - y
        for j in range(parameters):
            term = np.multiply(error, X[:, j])
            temp[0, j] = theta[0, j] - ((alpha / len(X)) * np.sum(term))
        theta = temp
        cost[i] = computeCost(X, y, theta)
    return theta, cost

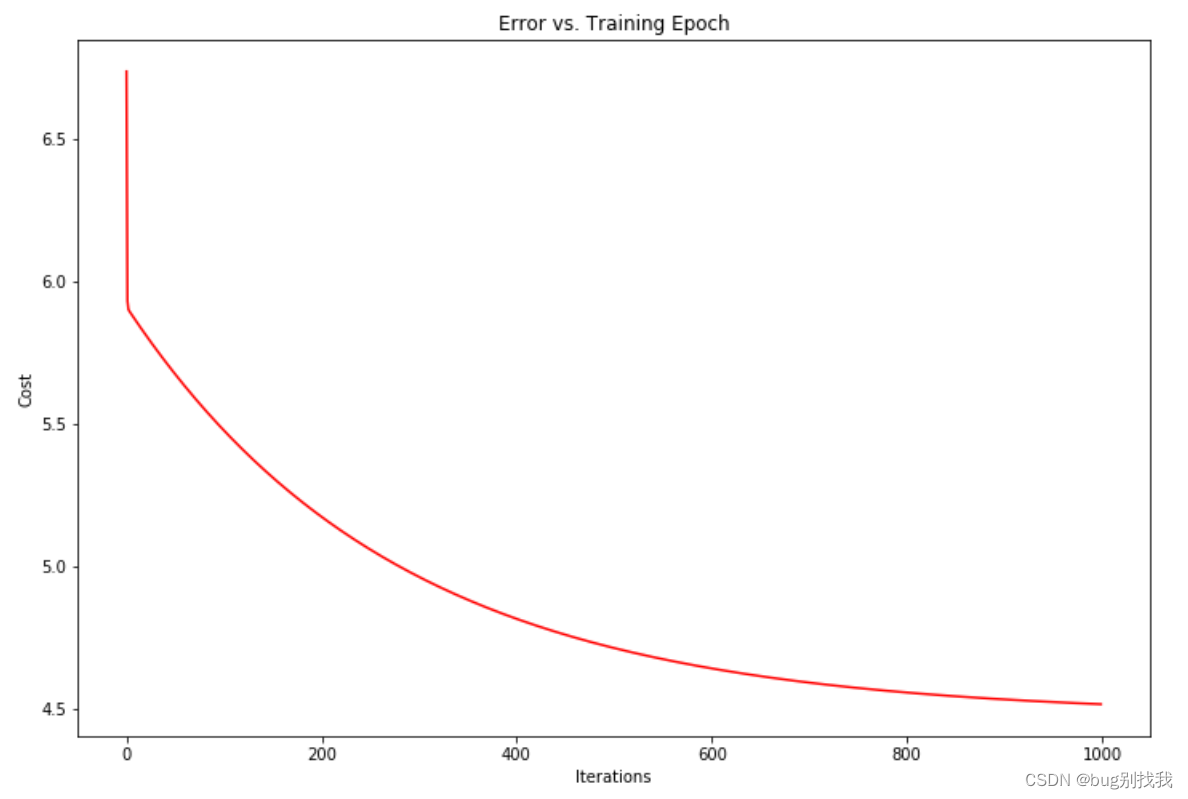
将梯度下降函数中得到的代价函数绘制出来可以看出，这是一个明显的凹函数，意味着代价函数是明显减小的

总结

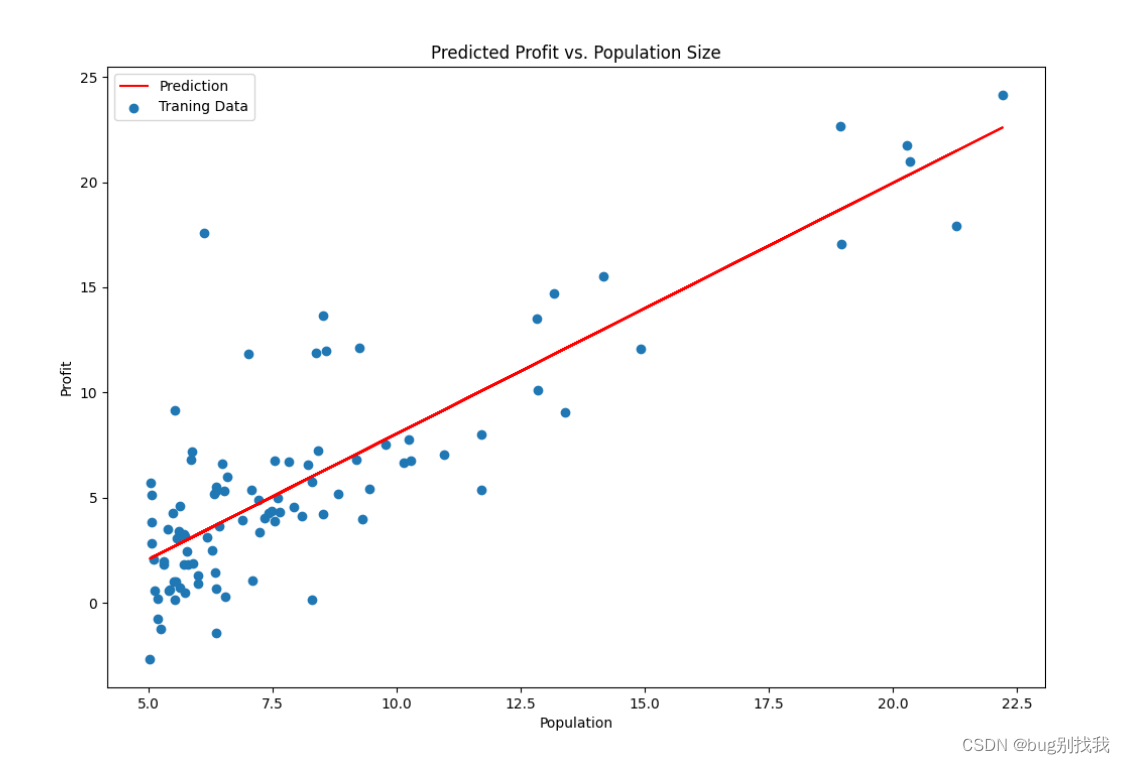
结果如下