差分
差分介绍
结论:差分是前缀和的逆运算
举例
一维差分
//一维前缀和 a[i]部分就是一维差分数组
s[i] = s[i-1]+a[i];
//一维差分
a[i] = s[i]-s[i-1];
二维差分
//二维前缀和 a[i][j]部分就是一维差分数组
s[i][j] = s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j];
//二维差分
a[i][j] = s[i][j]-s[i-1][j]-s[i][j-1]+s[i-1][j-1];
差分用法
用在一维子区间里的数都增减一个固定值,把对于区间内每个数的操作转换为对于差分数组中的端点的操作,时间复杂度降为o(1)。
用在二维子矩阵里的数都增减一个固定值,把对于子矩阵的每个数的操作转换为对应差分二维数组各个端点的操作。
总体思想就是在需要处理的区间范围内增减一个固定值,在影响到的其他范围内需要恢复,即相反操作。
举例
一维差分
差分数组在左端点增加c之后,会影响以其开始前缀和都增加c。所以为了确保只有LR这段增加c,需要从R+1开始减少c,即差分数组在R+1处减去c。
b[l]+=c;
b[r+1]-=c;
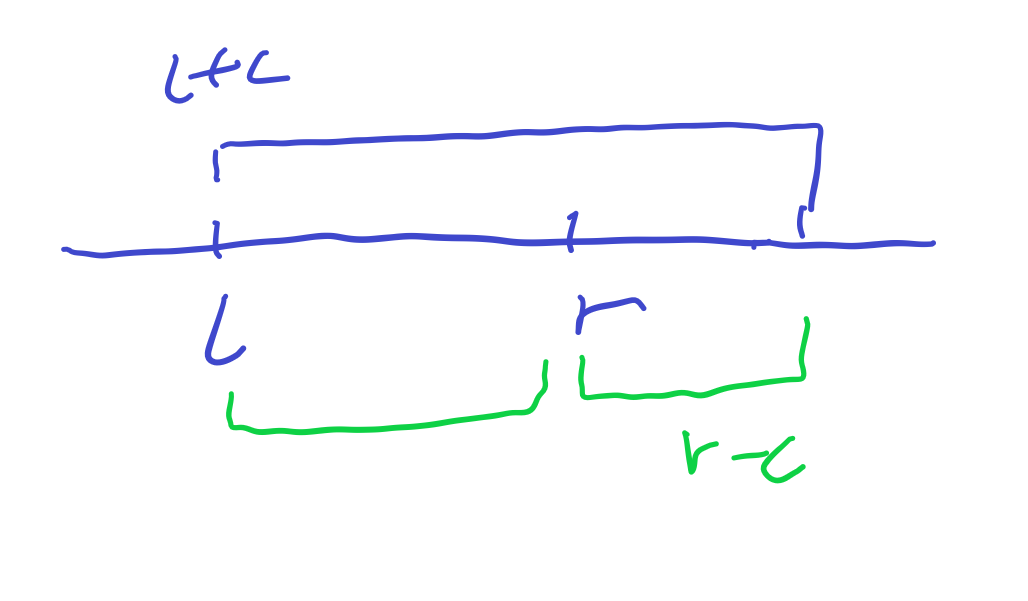
二维差分
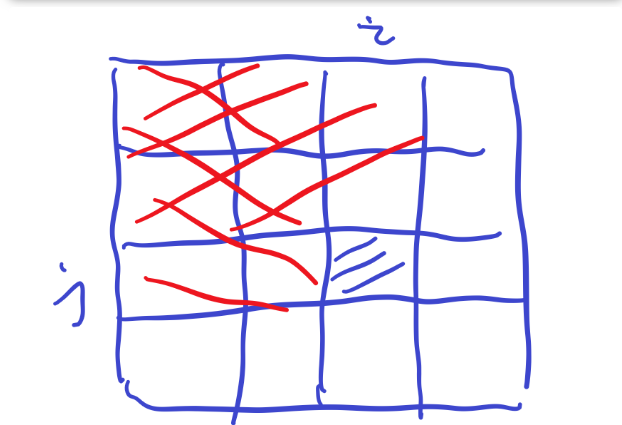
在 二维差分数组(x1,y1)增加会使得以(x1,y1)(n,m)范围内所有的数都增加c。所以为了确保只有(x1,y1)-(x2,y2)范围内数值增加c,则需要消除绿色部分的影响,做逆向操作。
b[x1][y1] += c;
b[x1][y2+1] -= c; //逆操作1
b[x2+1][y1] -= c;//逆操作2
b[x2+1][y2+1] +=c;//这块区域在逆操作1和2中减了两次,所以需要加上一次
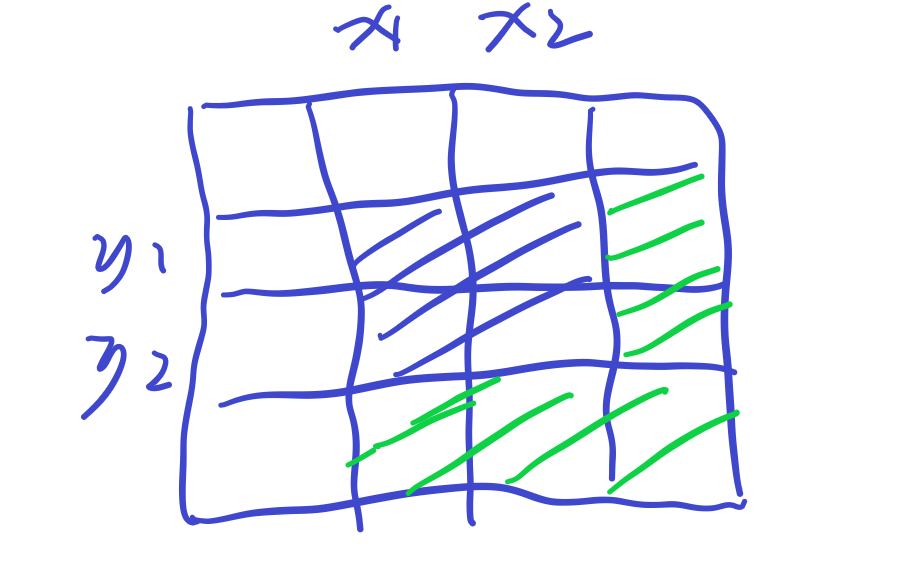
差分使用技巧
朴素思维
正常想法会先接收初始数组的输入,然后再计算每个差分数组。
一维数组
for(int i=1;i<=n;i++){
cin >> a[i];
b[i] = a[i]-a[i-1];
}
while(q--){
int l,r,c;
cin >>l>>r>>c;
b[l] +=c;
b[r+1] -=c;
}
二维数组
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++){
cin >>a[i][j];
b[i][j] = a[i][j]-a[i-1][j]-a[i][j-1]+a[i-1][j-1];
}
while(q--){
int x1,y1,x2,y2,c;
cin >>x1>>y1>>x2>>y2>>c;
b[x1][y1] +=c;
b[x1][y2+1] -=c;
b[x2+1][y1] -=c;
b[x2+1][y2+1] +=c;
}
简化思维
把全0当做初始数组,即初始的差分数组都是0,。接收输入的时候就执行差分数组的修改操作,当接收问询的时候 也当做是执行差分数组的修改操作。这样就不用额外计算差分数组的具体值。
一维数组
void insert(int l,int r,int c){
b[l] +=c;
b[r+1] -=c;
}
for(int i=1;i<=n;i++){
cin >> a[i];
insert(i,i,a[i]); //起始点i到结束点i,只有一个元素的区间
}
while(q--){
int l,r,c;
cin >>l>>r>>c;
insert(l,r,c);c
}
二维数组
void insert(int x1,int y1,int x2,int y2,int c){
b[x1][y1] +=c;
b[x1][y2+1] -=c;
b[x2+1][y1] -=c;
b[x2+1][y2+1] +=c;
}
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++){
cin >>a[i][j];
insert(i,j,i,j,a[i][j]); //起始点(i,j)到(i,j)只有一个元素的矩阵
}
while(q--){
int x1,y1,x2,y2,c;
cin >>x1>>y1>>x2>>y2>>c;
insert(x1,y1,x2,y2,c);
}
前缀和
前缀和分类
前缀和大体可以分为一维数组的前缀和和二维数组的前缀和。二维数组主要适用场景是矩阵相关的运算。
一维数组的前缀和
s[i] =s[i-1]+a[i]
二维数组的前缀和
总体思想:先计算以(1,1)为起始点 到各个点的区域总和,再用差值法计算给定的起始点到终点的区域总和
计算以(1,1)起始点的区域的总和
//计算s[i][j]的值
s[i][j] = s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j];
计算给定区域的总和
//计算(x1,y1)到(x2,y2)区域的值
s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1]; //中间-1的部分都是起始点(x1,y1)的坐标