课程地址和说明
线性回归p1
本系列文章是我学习李沐老师深度学习系列课程的学习笔记,可能会对李沐老师上课没讲到的进行补充。
线性回归
如何在美国买房(经典买房预测问题)

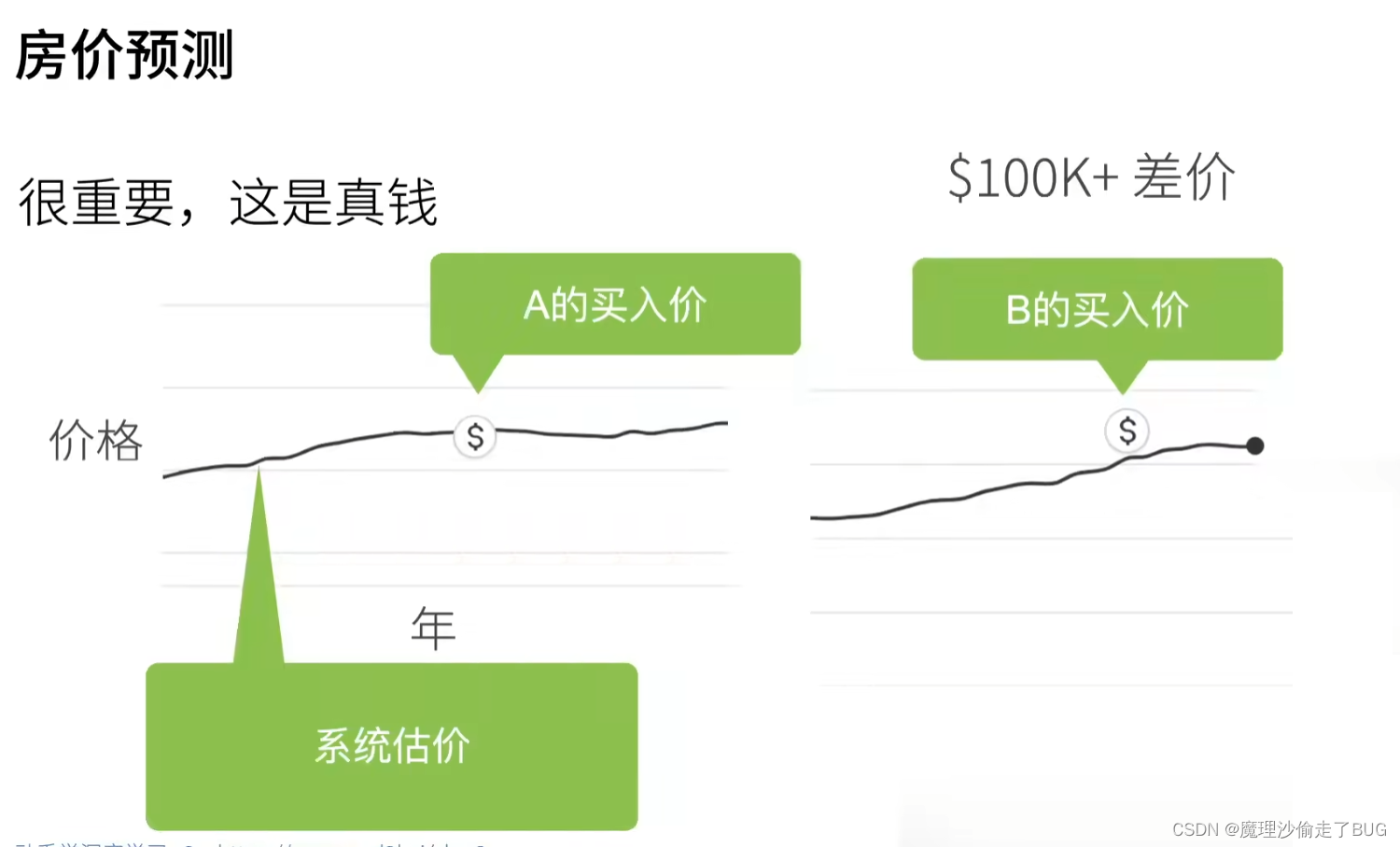
一个简化的模型

线性模型

其中,
- x → = [ x 1 , x 2 , … , x i , … , x n ] T \overrightarrow {x}=\left [ x_{1},x_{2},\dots ,x_{i} ,\dots ,x_{n}\right ]^{T} x=[x1,x2,…,xi,…,xn]T, i i i代表第 i i i个特征(即本例中的卧室个数,卫生间个数和居住面积),其实为了方便记录第 j j j个样本的第 i i i个特征,我更倾向于这个写法: x j → = [ x j 1 , x j 2 , … , x j i , … , x j n ] T \overrightarrow {{x}_{j}}=\left [ x_{j}^{1},x_{j}^{2},\dots ,x_{j}^{i} ,\dots ,x_{j}^{n}\right ]^{T} xj=[xj1,xj2,…,xji,…,xjn]T,其中 j j j代表第 j j j个样本, i i i代表第 j j j个样本的第 i i i个特征,下面的章节这样写比较方便;
- w → = [ w 1 , w 2 , … , w i , … , w n ] T \overrightarrow {w}=\left [ w_{1},w_{2},\dots ,w_{i} ,\dots ,w_{n}\right ]^{T} w=[w1,w2,…,wi,…,wn]T, w i w_{i} wi是代表着第 i i i个特征的重要程度(即权重),假如卧室个数 x 1 x_{1} x1比卫生间个数 x 2 x_{2} x2的重要程度大,则 w 1 > w 2 w_{1}>w_{2} w1>w2;
- b b b代表着模型的标量偏差。
【提问】解释一下线性回归模型的标量偏差
【chatGPT回答】线性回归模型中的标量偏差(scalar bias)通常是指模型中的一个额外参数,用来调整模型的输出,使其更好地拟合数据。这个偏差值是一个常数,不依赖于输入特征,它在线性回归模型中起到平移或偏移输出的作用。
线性回归模型用于建立输入特征和输出目标之间的关系,通常表示为:
y = w x + b y = wx + b y=wx+b
其中:
- y y y 是模型的输出(预测值)。
- x x x 是输入特征。
- w w w 是特征的权重或系数,用来衡量特征对输出的影响。
- b b b 是标量偏差,也称为截距或偏移项,它表示当输入特征 (x) 为零时,模型的输出 (y) 的期望值。
标量偏差 (b) 允许模型在没有输入特征的情况下仍然能够有一个非零的输出。这对于捕捉数据中的整体偏移或平移是很重要的。例如,如果你正在建立一个房价预测模型,特征 (x) 可能表示房屋的大小,但即使房屋大小为零,房价也不应该为零,因此标量偏差 (b) 允许模型预测一个基本价格。
在训练线性回归模型时,模型会尝试学习最佳的权重 (w) 和偏差 (b) 的值,以最小化预测值与真实值之间的差距(损失函数)。这个过程通常使用最小二乘法来完成。
总之,线性回归模型的标量偏差是一个用来平移或偏移模型输出的常数参数,它允许模型在没有输入特征时仍能够产生非零的输出,从而更好地拟合数据。
- 加权和(也就是预测值): y = w 1 x 1 + w 2 x 2 + ⋯ + w n x n + b = [ w 1 w 2 … w n ] ⋅ [ x 1 x 2 … x n ] = < w → , x → > + b y=w_{1}x_{1}+w_{2}x_{2}+\dots+w_{n}x_{n}+b=\begin{bmatrix} w_{1} & w_{2} & \dots & w_{n} \end{bmatrix}\cdot \begin{bmatrix} x_{1} \\ x_{2} \\ \dots \\ x_{n} \end{bmatrix}=<\overrightarrow {w},\overrightarrow {x}>+b y=w1x1+w2x2+⋯+wnxn+b=[w1w2…wn]⋅ x1x2…xn =<w,x>+b,其中 < w → , x → > <\overrightarrow {w},\overrightarrow {x}> <w,x>为 w → \overrightarrow {w} w与 x → \overrightarrow {x} x的内积,内积符号表示中两个向量的位置可以换的,即 < w → , x → > = < x → , w → > <\overrightarrow {w},\overrightarrow {x}>=<\overrightarrow {x},\overrightarrow {w}> <w,x>=<x,w>,其实我更喜欢将预测值记为 y ^ = < w → , x → > + b \hat {y}=<\overrightarrow {w},\overrightarrow {x}>+b y^=<w,x>+b,后面会看到我为什么这样记录。
线性模型可以看做是单层神经网络

神经网络源于神经科学

衡量预估质量


训练数据

其中,
- 矩阵 X \bm{X} X的每一个行向量 x i → T , i = 1 , 2 , … , n \overrightarrow {x_{i}}^{T},i=1,2,\dots ,n xiT,i=1,2,…,n都代表着第 i i i个样本,本来 x i → \overrightarrow {x_{i}} xi都是列向量,但是 X = [ x 1 → , x 2 → , … , x i → , … , x n → ] T = [ x 1 → T x 2 → T ⋮ x i → T ⋮ x n → T ] \bm{X}=\left [ \overrightarrow {x_{1}},\overrightarrow {x_{2}},\dots ,\overrightarrow {x_{i}} ,\dots ,\overrightarrow {x_{n}}\right ]^{T}=\begin{bmatrix} \overrightarrow {x_{1}}^{T} \\ \overrightarrow {x_{2}}^{T}\\ \vdots \\ \overrightarrow {x_{i}}^{T} \\ \vdots \\ \overrightarrow {x_{n}}^{T} \end{bmatrix} X=[x1,x2,…,xi,…,xn]T= x1Tx2T⋮xiT⋮xnT ,所以 x i → T \overrightarrow {x_{i}}^{T} xiT与 x i → \overrightarrow {x_{i}} xi都代表第 i i i个样本,其样本向量中的各个分量即是这第 i i i个样本的各个特征;
- y → = [ y 1 , y 2 , … , y i , … , y n ] T \overrightarrow{y}=\left [ y_{1},y_{2},\dots ,y_{i} ,\dots ,y_{n}\right ]^{T} y=[y1,y2,…,yi,…,yn]T代表了所有真实值(本例为真实房价)的数据集合,其中 y i , i = 1 , 2 , … , n y_{i},i=1,2,\dots ,n yi,i=1,2,…,n代表第 i i i个样本 x i → \overrightarrow {x_{i}} xi对应的真实值。
参数学习

其中
- 根据上面提到的平方损失的定义,训练损失函数写为:
ℓ ( X , y → , w → , b ) = 1 2 n ∑ i = 1 n ( y i − y ^ i ) 2 = 1 2 n ∑ i = 1 n ( y i − ( ( < w → , x i → > + b ) ) ) 2 = 1 2 n ∑ i = 1 n ( y i − < w → , x i → > − b ) 2 \ell (\textbf{X},\overrightarrow {y},\overrightarrow {w},b)=\frac{1}{2n}\sum\limits_{i=1}^{n} \left ( y_{i}-\hat{y}_{i} \right )^{2}=\frac{1}{2n}\sum\limits_{i=1}^{n} \left ( y_{i}-((<\overrightarrow {w},\overrightarrow {x_{i}}>+b)) \right )^{2} =\frac{1}{2n}\sum\limits_{i=1}^{n} \left ( y_{i}-<\overrightarrow {w},\overrightarrow {x_{i}}>-b \right )^{2} ℓ(X,y,w,b)=2n1i=1∑n(yi−y^i)2=2n1i=1∑n(yi−((<w,xi>+b)))2=2n1i=1∑n(yi−<w,xi>−b)2
图中的
b
b
b应为
b
→
=
(
b
,
b
,
.
.
.
,
b
)
n
×
1
T
\overrightarrow {b}=(b,b,...,b)^{T}_{n\times 1}
b=(b,b,...,b)n×1T,否则不符合数学上的定义,李沐老师之所以这么写是因为在PyTorch中,向量减去标量相当于对向量的每一个分量都减去相同的标量,所以上述公式在写代码时可以直接用,以下给出我推导的过程:

- a r g arg arg表示的是取什么什么值, a r g m i n arg min argmin指的是取最小值,图中的意思是找到使得损失函数 ℓ ( X , y → , w → , b ) \ell (\textbf{X},\overrightarrow {y},\overrightarrow {w},b) ℓ(X,y,w,b)的参数 w → ∗ , b ∗ \overrightarrow {w}^{*},b^{*} w∗,b∗.
显示解
因为我们用的是线性模型,所以我们有显示解。

【注】在评论区发现李沐老师少写了个转置,这里直接更正一下
将
X
\bm{X}
X进行增广,
w
→
\overrightarrow {w}
w进行增广,最终变为
X
n
×
(
m
+
1
)
,
w
→
(
m
+
1
)
×
1
\bm{X}_{n\times (m+1)},\overrightarrow {w}_{(m+1)\times 1}
Xn×(m+1),w(m+1)×1,则变为:

由链式求导法则和公式当
y
=
∣
∣
x
→
∣
∣
2
=
(
∑
i
=
1
m
x
i
2
)
2
=
(
x
1
2
+
x
2
2
+
⋯
+
x
m
2
)
2
=
x
1
2
+
x
2
2
+
⋯
+
x
m
2
y=||\overrightarrow x||^2=(\sqrt{\sum\limits_{i=1}^{m} x_{i}^{2}})^{2}=(\sqrt{x_{1}^{2}+x_{2}^{2}+\dots +x_{m}^{2}})^{2}=x_{1}^{2}+x_{2}^{2}+\dots +x_{m}^{2}
y=∣∣x∣∣2=(i=1∑mxi2)2=(x12+x22+⋯+xm2)2=x12+x22+⋯+xm2时,有:
∂
y
∂
x
→
=
[
∂
f
(
x
→
)
∂
x
1
∂
f
(
x
→
)
∂
x
2
⋮
∂
f
(
x
→
)
∂
x
m
]
m
×
1
=
[
2
x
1
2
x
2
⋮
2
x
m
]
m
×
1
=
2
x
→
\frac{\partial {y}}{\partial\overrightarrow x}=\begin{bmatrix} \frac{\partial {f(\overrightarrow x)}}{\partial{x_{1}}}\\ \frac{\partial {f(\overrightarrow x)}}{\partial{x_{2}}}\\ \vdots \\ \frac{\partial {f(\overrightarrow x)}}{\partial{x_{m}}} \end{bmatrix}_{m\times 1}=\begin{bmatrix} 2x_{1}\\ 2x_{2}\\ \vdots \\ 2x_{m} \end{bmatrix}_{m\times 1}=2\overrightarrow x
∂x∂y=
∂x1∂f(x)∂x2∂f(x)⋮∂xm∂f(x)
m×1=
2x12x2⋮2xm
m×1=2x
可知,

总结