GAN+FLOW+VAE的任务都可以用diffusion model来做
生成模型的5类：

• seq2seq自回归编码
• GAN
• FLOW(数学原理严谨，是个可逆的过程，但需要设计一些巧妙的结构来使得其可解)
• VAE
• Diffusion

一，条件概率公式与高斯分布的KL散度+重参数技巧

1. 条件概率的一般形式

   $P(A,B,C)=P(C|B,A)P(B,A)=P(C|B,A)P(B|A)P(A)$

   $P(B,C|A)=P(B|A)P(C|A,B)$

2. 基于马尔科夫假设的条件概率

   如果满足马尔科夫链关系$A\to B\to C$,则有：

   $P(A,B,C)=P(C|B,A)P(B,A)=P(C|B,A)P(B|A)P(A)=P(C|B)P(B|A)P(A)$

   $P(B,C|A)=P(B|A)P(C|A,B)=P(B|A)P(C|B)$

3. 高斯分布的KL散度公式

   对于两个单一变量的高斯分布 $p$ 和 $q$ 而言，它们的KL散度为：

   $$KL(p,q)=log\frac{{\sigma }_2}{{\sigma }_1}+\frac{{\sigma }^2+({\mu }_1-{\mu }_2{)}^2}{2{\sigma }_2^2}-\frac{1}{2}$$
   推导可以看这篇____高斯分布的KL散度公式

4. 重参数技巧
   如果想从高斯分布$N(\mu ,{\sigma }^2)$中采样，可以先从标准分布$N(0,1)$采样出 $z$ , 再得到 $\sigma \ast z+\mu$.这样做的好处是：将随机性转移到了 $z$ 这个常量上，而 $\sigma$和$\mu$则当做仿射变换网络的一部分。

$\sigma \ast z$就把随机性加到了标准差$\sigma$ 上， $z$ 取0附近的值的概率最大，$\sigma \ast z+\mu$ 就相当于在$N(\mu ,\sigma )$中采样了

二，VAE和多层VAE回顾

单层VAE的原理公式与置信下界

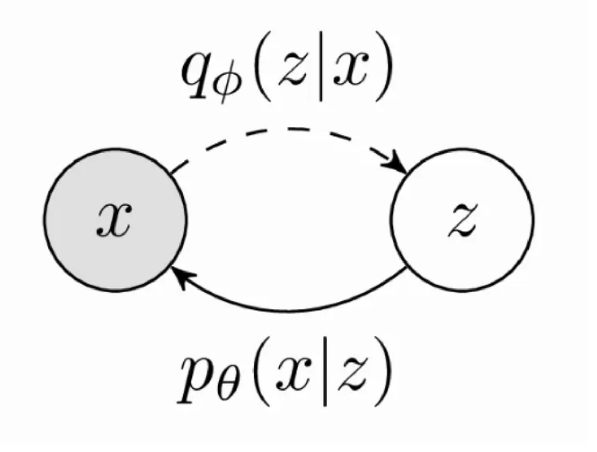
$x->z$为后验，训练的过程，train
$z->x$为inference过程，(丢掉train的过程)
$$p(x)={\int }_z{p}_{\theta }(x,z)dz={\int }_z{p}_{\theta }(x|z)p(z)dz$$
$$p(x)=\int q_{\varphi }(z|x).\frac{p_{\theta }(x|z)p(z)}{q_{\varphi }(z|x)}dz={\mathbb{E}}_{z\sim q_{\varphi }(z|x)}\left[\frac{p_{\theta }(x|z)p(z)}{q_{\varphi }(z|x)}\right]$$
$$logp(x)=log{\mathbb{E}}_{z\sim q_{\varphi }(z|x)}\left[\frac{p_{\theta }(x|z)p(z)}{q_{\varphi }(z|x)}\right]\stackrel{JenseInequality}{\ge }{\mathbb{E}}_{z\sim q_{\varphi }(z|x)}\left[log\frac{p_{\theta }(x|z)p(z)}{q_{\varphi }(z|x)}\right]$$
所以：
$$logp(x)\ge \underset{ELBO}{\underbrace{{\mathbb{E}}_{z\sim q_{\varphi }(z|x)}\left[log\frac{p_{\theta }(x|z)p(z)}{q_{\varphi }(z|x)}\right]}}$$

目的：使得$x$出现的概率最大，即要最大化$logp(x)$,那有Jensen不等式求得了$logp(x)$的下界，现在只需要最大化下界即可。最大化下界了，那$logp(x)$也就最大化了。即至此为止，我们要优化的目标函数已经找到了。
Jensen不等式：
$$log\sum _i{\lambda }_i{y}_i\ge \sum _i{\lambda }_{i}log{y}_i其中，{\lambda }_i\ge 0,\sum _i{\lambda }_i=1$$

下界：
$$\begin{array}{rl}& {\mathbb{E}}_{z\sim q_{\varphi }(z|x)}\left[log\frac{p_{\theta }(x|z)p(z)}{q_{\varphi }(z|x)}\right]\\ & ={\mathbb{E}}_{z\sim q_{\varphi }(z|x)}\left[log{p}_{\theta }(x|z)-log\frac{q_{\varphi }(z|x)}{p(z)}\right]\\ & ={\mathbb{E}}_{z\sim q_{\varphi }(z|x)}\left[\underset{由inference可以容易得到}{\underbrace{log{p}_{\theta }(x|z)}}\right]-\underset{KL(q_{\varphi }||p)}{\underbrace{\int q_{\varphi }(z|x)log\frac{q_{\varphi }(z|x)}{p(z)}}}\end{array}$$
一般假设$p,q$均为高斯分布，所以整个单层的VAE是可以求解的

多层VAE的原理公式与置信下界

分子分母同乘一个后验分布？？？？？？

$$p(x)={\int }_{z_1}{\int }_{z_2}{p}_{\theta }(x,z_1,z_2)d{z}_1,d{z}_2$$
$$p(x)=\iint q_{\varphi }\left(z_1,z_2\mid x\right)\frac{p_{\theta }\left(x,z_1,z_2\right)}{q_{\varphi }\left(z_1,z_2\mid x\right)}d{z}_1,d{z}_2={\mathbb{E}}_{z_1,z_2\sim q_{\varphi }\left(z_1,z_2\mid x\right)}\left[\frac{p_{\theta }\left(x,z_1,z_2\right)}{q_{\varphi }\left(z_1,z_2\mid x\right)}\right]$$
$$\log p(x)\ge \underset{ELBO}{\underbrace{{\mathbb{E}}_{z_1,z_2\sim q_{\varphi }\left(z_1,z_2\mid x\right)}\left[\log \frac{p_{\theta }\left(x,z_1,z_2\right)}{q_{\varphi }\left(z_1,z_2\mid x\right)}\right]}}$$
$$q(z_1,z_2|x)=q(z_1|x)q(z_2|z_1,x)\stackrel{马尔科夫性质}{=}q(z_1|x)q(z_2|z_1)$$
同理：
$$p(x,z_1,z_2)=p(x|z_1)p(z_1|z_2)p(z_2)$$

所以多层VAE的目标函数为：$\mathcal{L}(\theta ,\varphi )$

$$\mathcal{L}(\theta ,\varphi )={\mathbb{E}}_{q\left(z_1,z_2\mid x\right)}\left[\log p\left(x\mid z_1\right)-\log q\left(z_1\mid x\right)+\log p\left(z_1\mid z_2\right)-\log q\left(z_2\mid z_1\right)+\log p\left(z_2\right)\right]$$

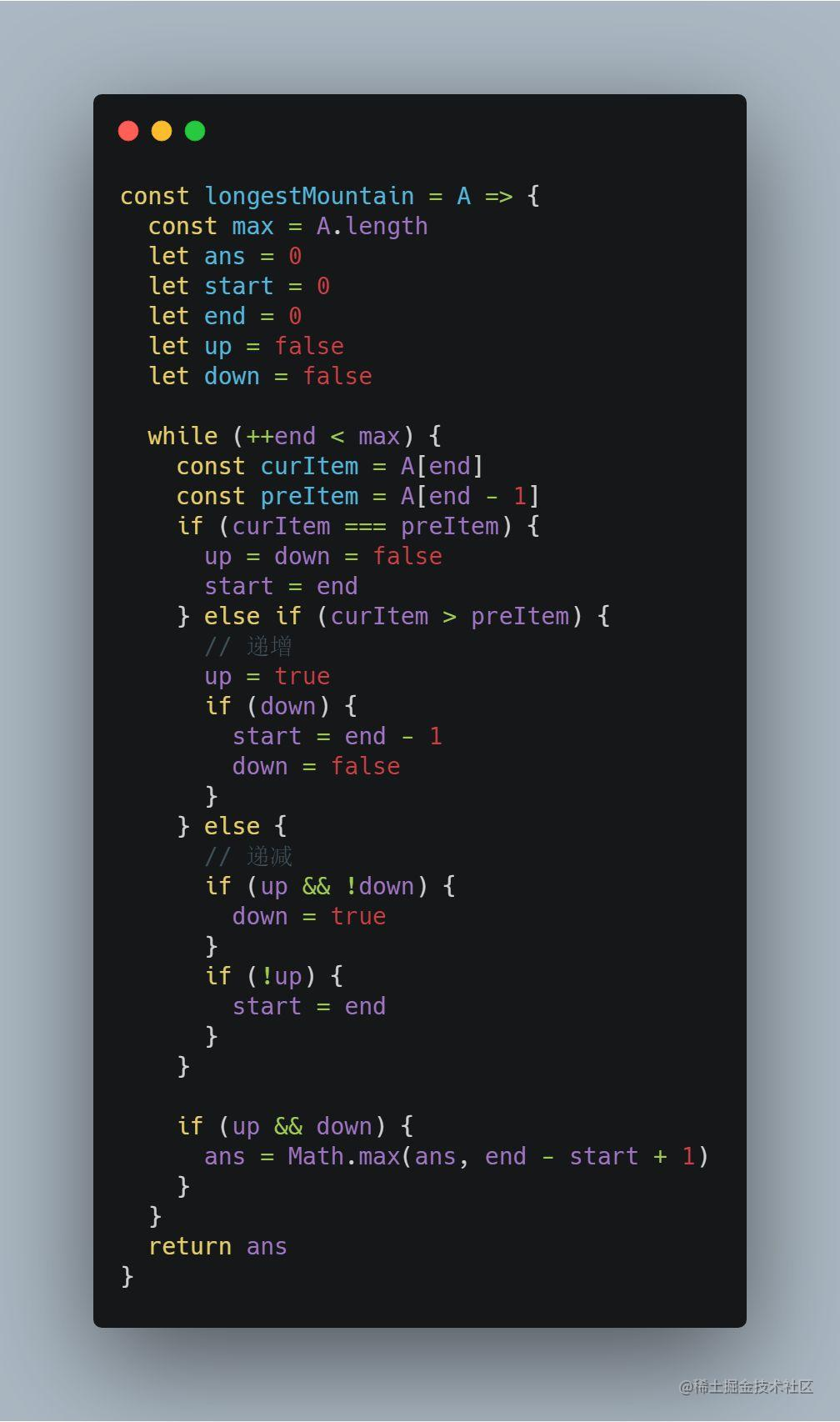
三，Diffusion Model 图示

Diffusion 的目标函数和多层VAE的目标函数很像。
从右往左：正向过程，q:条件概率分布(不含参数)，扩散过程，熵增过程，加噪过程，逐渐变为–>高斯分布
从左往右：反向过程/重建过程/生成过程：逆扩散过程，$p_{\theta }$：条件概率分布(含参数)，从噪声分布中推出目标分布，从目标分布中采样新样本，这样就可以生成新的图片。$在推理的时候只用到逆扩散过程$

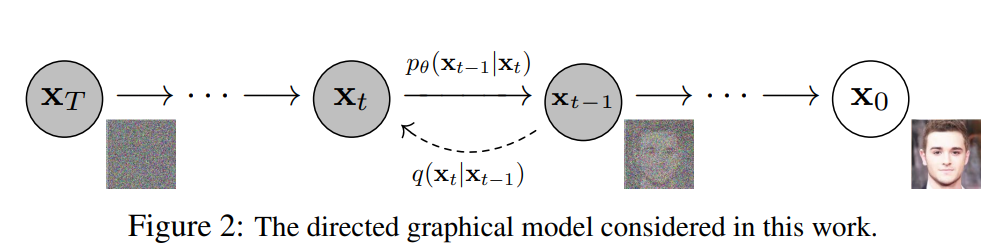
$目的:搞懂逆扩散过程是咋弄的，这样就可以由噪声来生成新图片了$

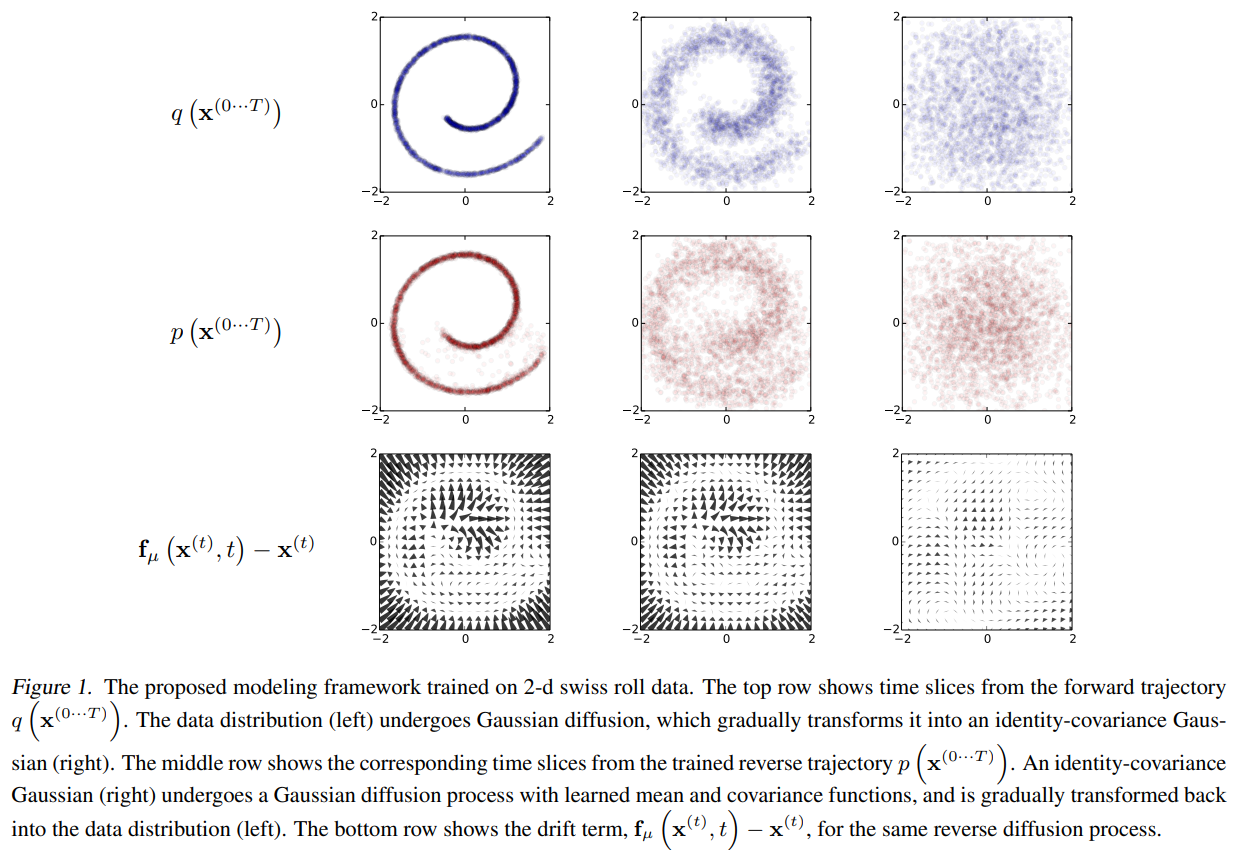
Figure1.瑞士卷图解：

第一行为从左到右：$q({\mathrm{x}}^{(0\cdots T)})$: pic–> noise加噪过程
第二行为从右到左：$p({\mathrm{x}}^{(0\cdots T)})$: noise->pic去噪过程
第三行为漂移量：$q和p之间的差$

四，扩散过程(Diffusion Process)

1. 给定初始数据分布$x_0\sim q(x)$, 可以不断地向分布中添加高斯噪声，此噪声的标准差是以固定值 ${\beta }_t$ 而确定的，均值是以固定值 ${\beta }_t$ 和当前 $t$ 时刻的数据 $x_t$ 决定的。这个过程是一个马尔科夫链过程。

$x_0\sim q(x)$即训练集服从$q(x)$分布，即扩散过程，${\beta }_t$是已知的，确定的(像learning rate)，，它不是通过网络预测的。扩散过程不含参数。

2. 随着 $t$ 的不断增大，最终数据分布 $x_T$ 变成了一个各项独立的高斯分布。

3. 任意时刻的$q(x_t)$推导也可以完全基于$x_0$和$\beta$来计算出来，而不需要做迭代。

注意：两个正态分布$X\sim N({\mu }_1,{\sigma }_1^2)$和$Y\sim N({\mu }_2,{\sigma }_2^2)$的叠加后的分布$aX+bY$的均值为$a{\mu }_1+b{\mu }_2$, 方差为$a^2{\sigma }_1^2+b^2{\sigma }_2^2$。所以$\sqrt{{\alpha }_t-{\alpha }_t{\alpha }_{t-1}}{z}_{t-2}+\sqrt{1-{\alpha }_t}{z}_{t-1}$可以重参数化成只含一个随机变量 $z$ 构成的 $\sqrt{1-{\alpha }_t{\alpha }_{t-1}}z$的形式。

A nice property of the above process is that we can sample ${\mathrm{x}}_{\mathrm{t}}$ at any arbitrary time step $t$ in a closed form using $\mathrm{reparameterization}\mathrm{trick}$. Let ${\alpha }_t=1-{\beta }_t$ and ${\bar{\alpha }}_t=\prod _{i=1}^t{\alpha }_i$

$q(x_t|x_{t-1})=\mathcal{N}(x_t;\sqrt{1-{\beta }_t}{x}_{t-1},{\beta }_{t}I),{\beta }_t$是方差，标准差是$\sqrt{{\beta }_t}$
$如何生成x_t呢？利用重参数技巧$
先从正态分布中生成一个$z_{t-1}$, 然后把 $\sqrt{{\beta }_t}.z_{t-1}+\sqrt{1-{\beta }_t}{x}_{t-1}$ 作为 $x_t$ 的一个采样值，不断迭代得到 $x_T$, 其中${\beta }_t$是随着$t$不断增加的。

$--------x_t的推导过程-----------$
$x_t=\sqrt{1-{\beta }_t}{x}_{t-1}+\sqrt{{\beta }_t}.z_{t-1}①$
$x_{t-1}=\sqrt{1-{\beta }_{t-1}}{x}_{t-2}+\sqrt{{\beta }_{t-1}}.z_{t-2}②$
令${\alpha }_t=1-{\beta }_t,{\bar{\alpha }}_t=\prod _{i=1}^t{\alpha }_i$,并将②带入①中得：$疑惑：那{\beta }_t应该代表是是方差吧，即{\sigma }^2$
$$\begin{array}{rl}{x}_t& =\sqrt{1-{\beta }_t}{x}_{t-1}+\sqrt{{\beta }_t}.z_{t-1}\\ & =\sqrt{{\alpha }_t}{x}_{t-1}+\sqrt{1-{\alpha }_t}.z_{t-1}\\ & =\sqrt{{\alpha }_t{\alpha }_{t-1}}{x}_{t-2}+\underset{重参数技巧}{\underbrace{\sqrt{{\alpha }_t(1-{\alpha }_{t-1})}{z}_{t-2}+\sqrt{1-{\alpha }_t}.z_{t-1}}}\\ & =\sqrt{{\alpha }_t{\alpha }_{t-1}}{x}_{t-2}+\sqrt{1-{\alpha }_t{\alpha }_{t-1}}{\bar{z}}_{t-2}\\ & =\cdots \\ & =\sqrt{{\bar{\alpha }}_t}{x}_0+\sqrt{1-{\bar{\alpha }}_t}z\end{array}$$

$q(x_t|x_0)=\mathcal{N}(x;\sqrt{{\bar{\alpha }}_t}{x}_0,(1-{\bar{\alpha }}_t)I)$,其中，方差为$(1-{\bar{\alpha }}_t)I$, 即${\sigma }^2$

因为所有的 $z$ 都是从正态分布$N(0,1)$中采样出来的，再由3中的两个正太分布的叠加提示得：
$Let{\bar{z}}_{t-2}=\left[\sqrt{{\alpha }_t(1-{\alpha }_{t-1})}{z}_{t-2}+\sqrt{1-{\alpha }_t}.z_{t-1}\right],then{\bar{z}}_{t-2}\sim \mathcal{N}(0,1-{\alpha }_t{\alpha }_{t-1})$
即$z_{t-1}\sim \mathcal{N}(0,1),z_{t-2}\sim \mathcal{N}(0,1)$，所以aX+bY的均值为：0，方差为：$1-{\alpha }_t{\alpha }_{t-1}$，即 ${\bar{z}}_{t-2}$ 也是从高斯分布中采样得到的
$-------------------$
总结：$x_t=\sqrt{{\bar{\alpha }}_t}{x}_0+\sqrt{1-{\bar{\alpha }}_t}{z}_t③$，那当T为多少时，$x_T$才能真变为各向独立的高斯分布呢？

即${\bar{\alpha }}_t\to 1,1-{\bar{\alpha }}_t\to 0$时，$q(x_t|x_0)=\mathcal{N}(x;\sqrt{{\bar{\alpha }}_t}{x}_0,(1-{\bar{\alpha }}_t)I)$变为标准的高斯分布 $\mathcal{N}(0,1)$, 由上式可以求出当$t=$何值时，$q(x_t|x_0)$约等于标准的高斯分布。

$为什么要让最后的q(x_t|x_0)约等于标准的高斯分布？$
因为让扩散过程扩散到最后，即不断加噪，然后最后变成标准高斯分布，这样逆扩散过程就可以由任意的一个标准高斯分布的初始状态通过逆扩散过程最后生成新的样本
Diffusion 过程完全不含参数
由式③得：只要给定初始分布$x_0$, 则任何时刻的采样值均可以算出，方法有两种：1.迭代；2.直接算(需要预先计算出${\alpha }_t$)

与VAE的区别：

VAE：

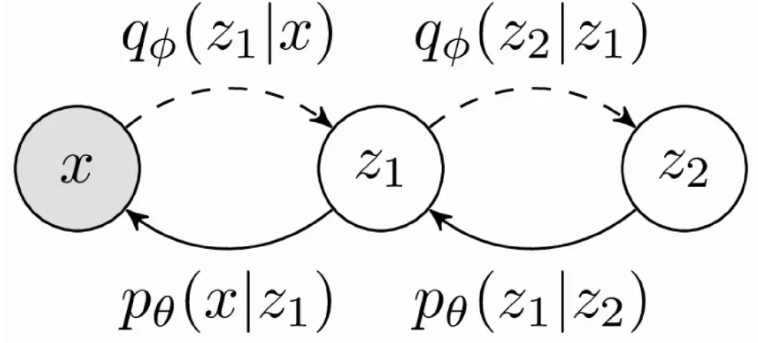
• $x\to z$并不是无参过程，而是通过后验网络给预测出来的
• $z$和$x$不一定完全无关，但diffusion model中最后的 $x_T$ 是一个标准的高斯分布，基本和$x_0$完全无关
• 在VAE中的$x$和$z$的维度可以不一样，但diffusion model中的$x_1,x_2,\cdots x_T$的维度始终保持不变。

如何设置扩散过程中的${\beta }_t$

当分布越来越接近于噪声分布时，可让${\beta }_t$增大，越来越大。同理，在$x_T\to x_0$逆扩散过程中, 最开始的几步可能还是噪声的模样，到最后面的几步就很快显示出图片的模样了。