弗洛伊德算法(Floyd)

之前介绍了迪杰斯特拉算法(Dijkstra)。具体请看：最短路径算法——简单明了的迪杰斯特拉算法(Dijkstra)。Dijkstra适用于非负权图，并且一次只能从网络中找源点到任何一个节点的最短路径，而Floyd算法的应用更加广泛，可以求网络中任意两点之间的最短路径，而且弗洛伊德算法适用于负权图，这篇文章就用图和表的形式来介绍一下弗洛伊德算法！

基本原理

Floyd算法可以给出网络中任意两个节点之间的最短路径，因此它是比Dijkstra更一般的算法。Floyd算法的思想是将n个节点的网络表示为n行n列的矩阵，而矩阵中的元素( i , j )表示从节点i到节点j的距离d_ij，如果两点直接没有边相连，则相应的元素就是无穷( ∞ )

算法步骤

第1步：定义初始距离矩阵D₀、节点序列矩阵S₀ ，如下表。对角线上用”—“表示不需要从自身到自身。
这里的节点序列矩阵相当于路线表，如下表，S_ij = j 表示从节点 i 到节点 j 只需经过节点j 即可。

第2步:一般的第k步：令第k行为枢轴行，第k列为枢轴列。对于矩阵D_k-1 （上一步完成后的矩阵）中对的每一个元素做三重操作。

如果满足条件：

d _ik +d_kj < d_ij (i !=k,j !=k,i !=j)

则进行下面的操作：

1. 用d_ik + d_kj 代替矩阵D_k−1 中的元素d_ij ，从而得到矩阵D_k
2. 用k代替矩阵S_k−1 中的元素s_ij ，从而得到矩阵S_k
3. 令k = k + 1 ，如果k = n + 1，停止，否则重复此步骤

过程图解

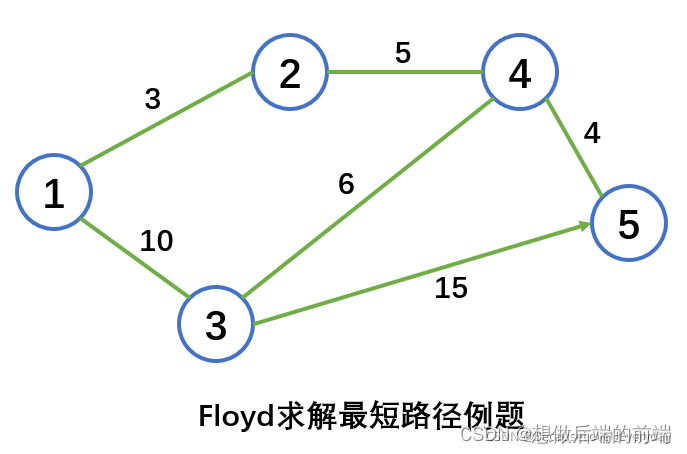
对图中的网络，求任意两个节点之间的最短路径，图中弧上给出了相应节点间的距离。弧(3,5)是有向的，其他边都是双边。

初始化配置表：

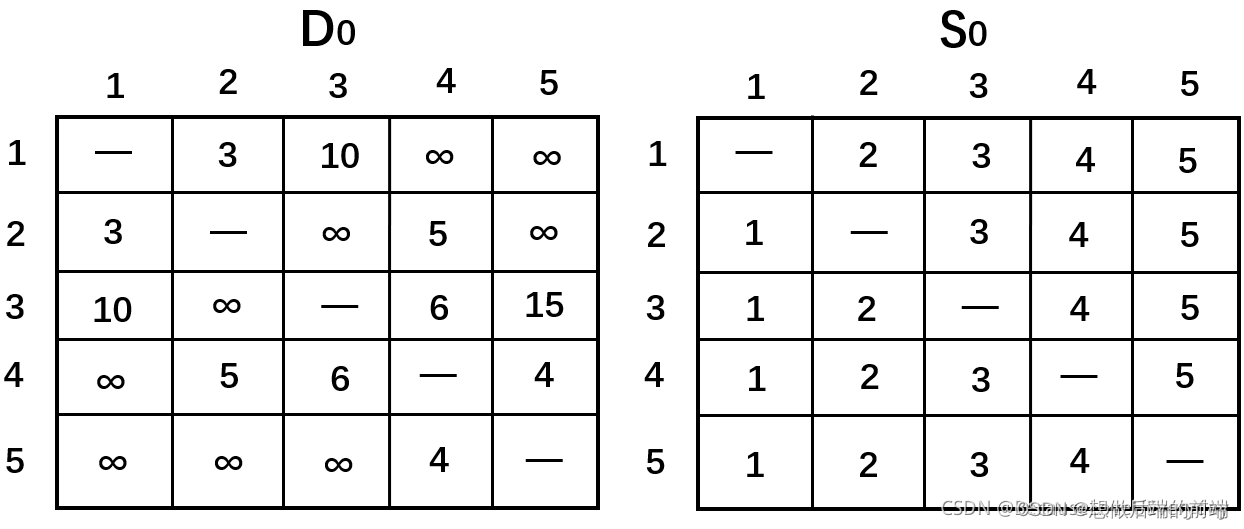
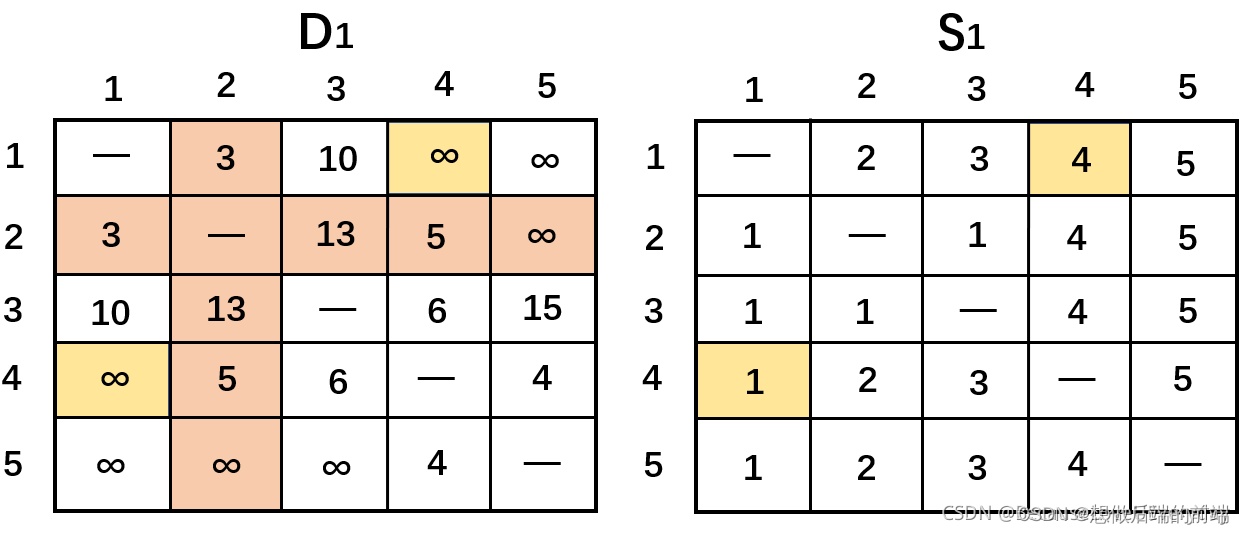
令k = 1，D₀矩阵中的黄色阴影表示的第1行和第1列为枢轴行和枢轴列。

根据三重操作发现可以改进的元素是d₂₃ 和d₃₂ ，即

(1) d₂₁ + d₁₃ = 3 + 10 = 13 < ∞ 则在d₂₃中用13 代替∞，并令s₂₃ = 1
(2) d₃₁ + d₁₂ = 10 + 3 = 13 < ∞ 则在d₃₂中用13 代替∞，并令s₃₂ = 1

令k = 2,D₀矩阵中的黄色阴影表示的第2行和第2列为枢轴行和枢轴列。
根据三重操作发现可以改进的元素是d₁₄和d₄₁，即

(1) d₂₁ + d₄₂ = 3 + 5 = 8 < ∞ 则在d₁₄中用8 代替∞，并令s₁₄ = 2
(2) d₂₄ + d₁₂ = 5 + 3 = 8< ∞ 则在d₄₁中用8 代替∞，并令s₄₁ = 2

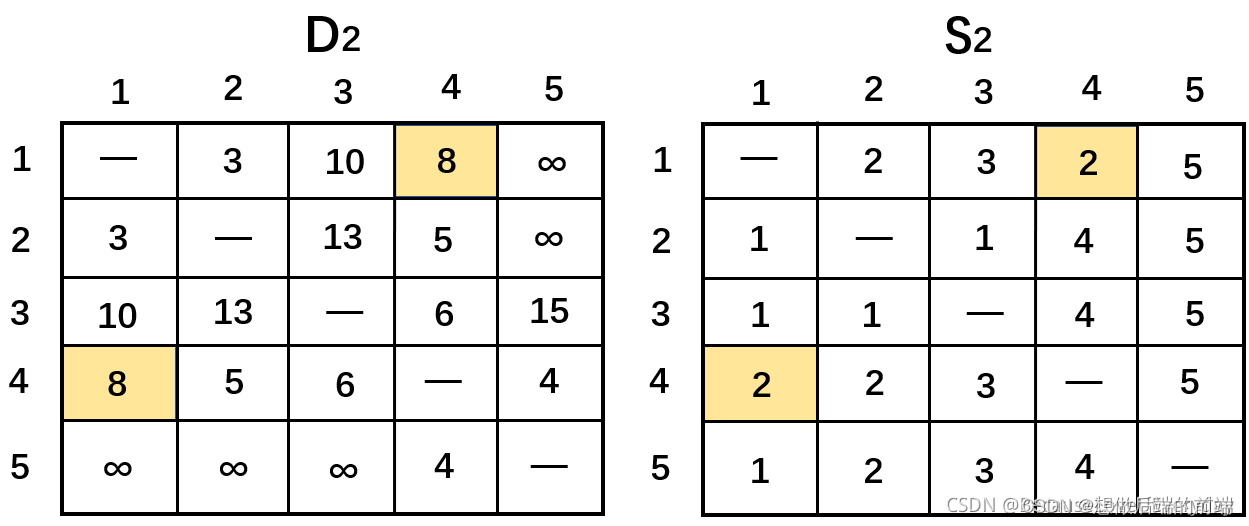
以此类推…

当k = 5，D₀ 矩阵中的黄色阴影表示的第5行和第5列为枢轴行和枢轴列。
根据三重操作发现没有可以改进的元素了。

这两个矩阵包含了网络中任意两个节点最短路径的所有信息。如从矩阵D中可以看出节点1到节点5的最短路径长度为12.从矩阵S中发现，节点1到节点5的中间节点是节点4，即节点1→节点4→节点5，再看节点1→节点4中间是节点2，即节点1需要通过节点2到达节点4，即节点1→节点2→节点4；而节点4可以直接到节点5，中间没有节点，因此可以得到节点1到节点5的最短路径是节点1→节点2→节点4→节点5.

完整代码

#include<iostream>
#include<vector>
#include<queue>
using namespace std;
 
#define MAXVEX 100//最大顶点数
typedef char VertexType;//顶点类型
typedef int EdgeType;//边上的权值类型
typedef struct
{
	VertexType vexs[MAXVEX];//顶点表
	EdgeType arc[MAXVEX][MAXVEX];//邻接矩阵
	int numVertexte;//当前顶点数
	int numEdges;//当前边数
}MGraph;
 
void ShortestPath_Floyd(MGraph G, vector<vector<int>>& P, vector<vector<int>>& D)
{
	for (int i = 0; i < G.numVertexte; ++i)
	{
		for (int j = 0; j < G.numVertexte; ++j)
		{
			D[i][j] = G.arc[i][j];//用G的邻接矩阵初始化D
			P[i][j] = j;
		}
 
		for (int i = 0; i < G.numVertexte; ++i)
		{
			for (int j = 0; j < G.numVertexte; ++j)
			{
				for (int w = 0; w < G.numVertexte; ++w)
				{
					if (D[j][w] > D[j][i] + D[i][w])//如果经过下标为i的顶点路径比原两点间路径更短
					{
						D[j][w] = D[j][i] + D[i][w];//更新D的值
						P[j][w] = P[j][i];//更新P的值
					}
				}
			}
		}
	}
}
 
/*我们可以通过下面这个函数将最短路径打印出来*/
void Print(MGraph G, vector<vector<int>>& P, vector<vector<int>>& D)
{
	for (int i = 0; i < G.numVertexte; ++i)
	{
		for (int j = i+1; j < G.numVertexte; ++j)
		{
			printf("v%d-v%d weight:%d ", i, j, D[i][j]);//打印源点 终点  以及他们之前的权
			int k = P[i][j];//第一个路径顶点下标
			printf(" path:%d", i);//打印源点
			while (k != j)//如果没有到终点
			{
				printf("-> %d", k);//打印路径顶点
				k = P[k][j];//获取下一个路径顶点下标
			}
			printf(" -> %d\n", j);//打印终点
		}
		printf("\n");
	}
}