[python 刷题] 22 Generate Parentheses

题目：

Given n pairs of parentheses, write a function to generate all combinations of well-formed parentheses.

这里 well-formed 指的就是合法的括号配对，这里会提两个解

第一个是暴力解，也就是找出所有括号的配对随后用 [JavaScript 刷题] 栈 - 有效的括号, leetcode 20 的解法进行验证即可

如当 n=3 的情况下，就会生成 ['((((((', '((((()', '(((()(', '(((())', '((()((', '((()()', '((())(', '((()))', '(()(((', '(()(()', '(()()(', '(()())', '(())((', '(())()', '(()))(', '(())))', '()((((', '()((()', '()(()(', '()(())', '()()((', '()()()', '()())(', '()()))', '())(((', '())(()', '())()(', '())())', '()))((', '()))()', '())))(', '()))))'] 中拼接方法，再调用 validate 去过滤不需要的数据，解法如下：

class Solution:
    def generateParenthesis(self, n: int) -> List[str]:
        res = ['(']
        for i in range(n * 2 - 1):
            temp = []
            for comb in res:
                temp.append(comb + '(')
                temp.append(comb + ')')
            res = temp

        def is_valid_parenthesis(s: str) -> bool:
            map_char = {'}': '{', ')': '(', ']': '['}
            stack = []

            for c in s:
                if c in map_char:
                    if not stack or stack.pop() != map_char[c]:
                        return False
                else:
                    stack.append(c)

            return len(stack) == 0

        return filter(is_valid_parenthesis, res)

这里代码我直接拿了 valid parenthesis 的题解，不过实际上对这一题来说只有 () 的配对

时间复杂度为 $O(n\times 2^{2n})$，其中生成所有节点的过程可以理解成一个二叉树的生成，因此遍历的时间复杂度为 $2^{2n}$，但是在生成节点的过程中还有一个 for 循环，因此就将时间复杂度拉成了 $O(n\times 2^{2n})$

简单的说就是，对于每个 $n$ 来说，最多可能有 $2^{2n}$ 个解，在 is_valid_parenthesis 这个阶段，会遍历 $n$ 个 $2^{2n}$ 解，因此时间复杂度为二者的乘积

空间复杂度也为 $O(n\times 2^{2n})$，也是出于同样的理由，需要保存所有 $n$ 个节点与其子 $2^{2n}$ 个节点

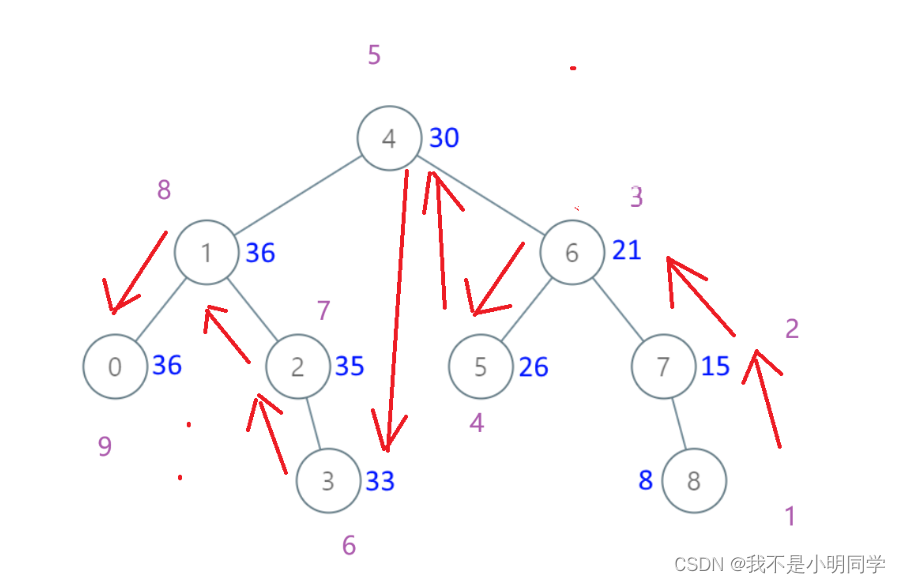
可视化一下就是这样：

现在再提出一个更加优化的解，暴力解是提出了所有可能的解，并且再对其进行便利，不过在构建子节点的时候，其实是有先决条件可以对子节点进行限制的，以 open 为 ( 的计数，close 为 ) 的计数：

• 当 open = close 时，只可能往子节点中添加 (

• 当 open = n 时，只可能往子节点中添加 )

• 只有当 open == close == n 时才是一个合法的结果

前二者可以有效控制时间复杂度，后者则是可以有效控制空间复杂度

可视化一下是这样：

代码为：

class Solution:
    def generateParenthesis(self, n: int) -> List[str]:
        res = []

        def backtrack(open: int, close: int, s: str):
            if open == close == n:
                res.append(s)
                return

            if open < n:
                backtrack(open + 1, close, s + '(')

            if close < open:
                backtrack(open, close + 1, s + ')')

        backtrack(0, 0, '')

        return res

这题的时间复杂度和空间复杂度为 $O(\frac{4^n}{\sqrt{n}})$，具体导出这里就不细说了，我怕把自己也绕进去

主要还是在两个 if 循环上，它排除了 open >= n 和 close >= open 的选项，这也是 $\frac{1}{\sqrt{n}}$ 的来源，基本上可以看到，所有的子树上选项被砍了一半

感兴趣的话可以推导一下 $C_n=\frac{2n!}{(n+1)!n!}$，不过距离我上一次学习数学已经是五六年前的事情了，为避免误人子弟就不一步步推了