动手学深度学习（pytorch版）第二章-2.3线性代数Note-linear-algebra

news2025/1/11 23:41:40

类型

标量：仅包含一个数值被称为标量

向量：向量可以被视为标量值组成的列表

矩阵：正如向量将标量从零阶推广到一阶，矩阵将向量从一阶推广到二阶。

A = torch.arange(20).reshape(5, 4)
A.T //转置

张量：是描述具有任意数量轴的n维数组的通用方法

X = torch.arange(24).reshape(2, 3, 4)

张量算法的基本性质

张量与张量

A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
B = A.clone()  # 通过分配新内存，将A的一个副本分配给B
#A, A + B，A*B //按元素相加 按元素相乘（Hadamard积）

张量与标量

a = 2
X = torch.arange(24).reshape(2, 3, 4)
a + X, (a * X).shape

降维常见运算

A.shape, A.sum()
A_sum_axis0 = A.sum(axis=0)
A.mean()// A.sum() / A.numel()

点积

给定两个向量 $\mathbf{x},\mathbf{y}\in\mathbb{R}^d$

$\mathbf{x}^\top \mathbf{y} = \sum_{i=1}^{d} x_i y_i$

torch.dot(x, y) //相当于torch.sum(x * y)

叉积

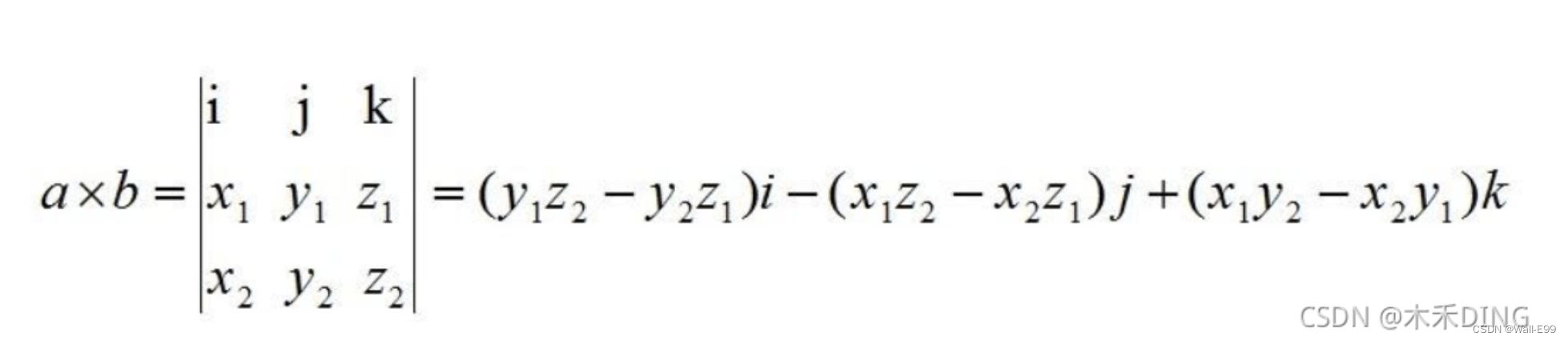
torch.cross(x, y)

矩阵-向量积

矩阵和向量相乘，使用`mv`函数，注意，`A`的列维数（沿轴1的长度）必须与`x`的维数（其长度）相同。

torch.mv(A, x)

矩阵-矩阵乘法

两个矩阵 $\mathbf{A} \in \mathbb{R}^{n \times k}$ 和 $\mathbf{B} \in \mathbb{R}^{k \times m}$

torch.mm(A, B)

范数

L1范数：

$\|\mathbf{x}\|_1 = \sum_{i=1}^n \left|x_i \right|$

torch.abs(u).sum()

L2范数：

$\|\mathbf{x}\|_2 = \sqrt{\sum_{i=1}^n x_i^2}$

u = torch.tensor([3.0, -4.0])
torch.norm(u)

L_p范数:

$\|\mathbf{x}\|_p = \left(\sum_{i=1}^n \left|x_i \right|^p \right)^{1/p}.$

Frobenius范数:

$\|\mathbf{X}\|_F = \sqrt{\sum_{i=1}^m \sum_{j=1}^n x_{ij}^2}$

torch.norm(torch.ones((4, 9)))

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1037356.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！