网格编码技术研究进展

1. VDMC编码技术

1.1 VDMC介绍

1.1.1 编码对象

具有时变拓扑的动态网格

1.1.2 技术细节

VDMC的编码和解码过程的高层框图如图2所示[4][5]。预处理模块提供了更好的率失真( Rate-Distortion，RD )性能，支持可伸缩解码和渐进传输等优点，可以选择应用。预处理模块将动态网格输入的第i帧(记为M(i))转换为一组基网格（即降分网格）m(i)与位移d(i)。关联属性图A(i)也做了相应的调整。编码器对这种新的表示进行压缩并生成压缩后的比特流b(i)，它包含各部分子比特流。注意，编码过程中的反馈回路允许编码器引导预处理块并根据各种准则改变其参数以达到最佳可能的折中，包括：率失真、编码/解码复杂度、随机访问、重构复杂度、终端能力、编码/解码功耗以及通信网络带宽和延迟。解码器块获取压缩后的比特流b(i)，提取各个子比特流，并进行解压缩，生成以下组件：重建基网格m′，重建位移d″，重建属性映射A′，补丁元数据。后处理模块对重建基网格运用线性插值，比如在边中点插入新的顶点，来对基网格进行超分（mesh subdivision），然后结合重建位移d″生成重建网格M″(i)，以及生成M″(i)的属性图A″(i)。该方法的主要精神在于编码端和解码端采用了约定的降分和超分方法，不需要额外传输信息，且编码端对原始网格降分后，大大节省了码率，并且将由降分网格超分后的网格与基础网格的位移，即残差，传输到解码端，从而以更紧凑的形式表征了复杂的网格细节。但是目前VDMC采用的线性插值超分技术过于朴素，常见的网格内容具有一定的形状特征，如头，手具有一些典型的特征。利用网络事先捕捉这些局部特征，然后再对网格进行非线性插值的超分，由此得到一个网格的智能超分算法替代VDMC的线性插值技术，理论上可以提高编码效率。

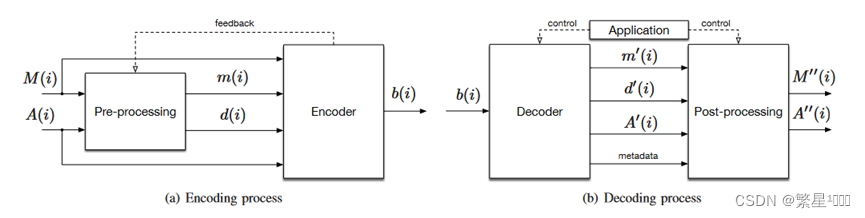
图1 VDMC的编解码流程高层框图

1.2 （2023 ICIP）INTER-FRAME CODING FOR DYNAMIC MESHES VIA TEMPORALLY-CONSISTENT RE-MESHING

关键思想: 网格的mapping算法改进帧内编码

引入鲁棒的帧内面映射框架对输入网格进行重新网格化，使其具有一一对应的顶点和面。因为V – DMC的帧间编码要求输入的网格序列具有恒定的拓扑结构。

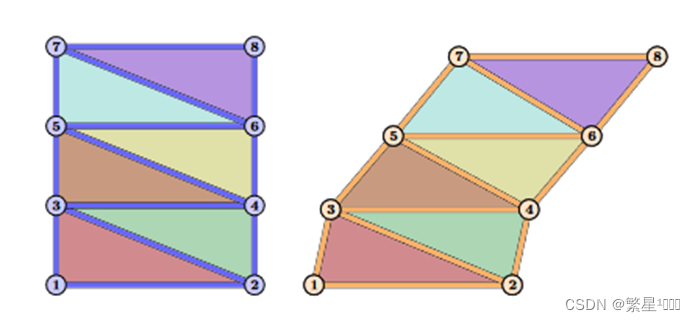
图2 点面一一对应的网格（恒定的拓扑）

技术细节

虽然输入网格具有时变的拓扑，但是我们可以创建一个双射结合面映射来连接两个输入网格，并重新划分目标网格以对应参考网格，使其拓扑时不变。

• 原来的问题：

原来的V_DMC也会对输入网格进行重网格化使其具有恒定拓扑，但是原来的帧内表面映射发方法不够鲁棒，且不直接适用于V - DMC所使用的数据。此外，网格重划分过程会引入几何畸变，降低编码效率。

• 主要贡献：
  • ( 1 )通过匹配关键点并将参考网格变形到目标网格表面，实现鲁棒的帧内面映射。
  • ( 2 )从参考网格和重划分后的当前网格生成一一对应顶点和面的基础网格的同步降采样方案。

帧内面映射算法Inter-surface mapping

• 关键点选择——ISS(intrinsic shape signatures)
  • 对$M(i)$中的每个点$ V_k $计算scatter matrix $\sum \left(V_k\right)=\frac{1}{N}{\sum }_{V_q\in \mathcal{N}\left(V_k\right)}\left(V_q-{\mu }_k\right){\left(V_k-{\mu }_k\right)}^{\top }$，$\sum (V_k)$:
  • 对$\sum (V_k)$特征值分解，特征值从大到小为${\lambda }_1,{\lambda }_2,{\lambda }_3$, 为了避免检测到沿主方向具有相似扩展的关键点,进行筛选：
    • 首先特征值需要满足：$\frac{{\lambda }_2}{{\lambda }_1}<{\gamma }_{12}\wedge \frac{{\lambda }_3}{{\lambda }_2}<{\gamma }_{23}$
    • 在剩下的点中：一个点在其邻域中若其${\lambda }_3$最小，则该点为关键点
• 对$M(i)$的每一个关键点在$M(j)$的关键点中寻找匹配点，根据 $\arg {\min }_{y_t}\mathrm{Er}\left(y_t\right)={\min }_{\mathbf{T}}\mathrm{Dis}\left(\mathcal{N}\left(y_t\right),\mathbf{T}\left(\mathcal{N}\left(x_l\right)\right)\right)$
• 对$M(i)$执行尽可能地刚体变换使其具有和$M(j)$一样的拓扑

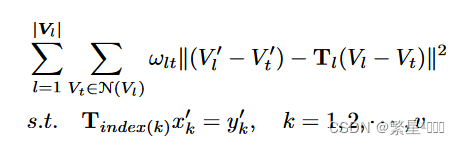
同步简化Simultaneous decimation

即mapping后的$M(i)$和$M(j)$有着相同的拓扑，但是如果分别简化，最后简化的mesh未必具有相同的拓扑，所以得同步简化。每次折叠边$e_k$的时候，要考虑两个mesh的折叠平方误差。$C_i$是边长，$X_i$是新插入顶点的位置。

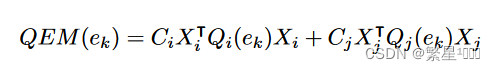
（2023 ICIP) HIERARCHICAL ARITHMETIC CODING OF DISPLACEMENTS FOR DYNAMIC MESH COMPRESSION

主要思想：位移矢量的分层算术编码

• 原来的问题
  太复杂了。视频编解码器中丰富的工具对于不相关的位移来说过于复杂。
• 主要贡献
  提出了分层算术编码，将系数层次分为块和更小的子块。当块/子块中所有的层都为零时，用一个标志位代替层进行编码。实验结果表明，在编码效率提高的同时，编码复杂度显著降低

技术细节

• 过程
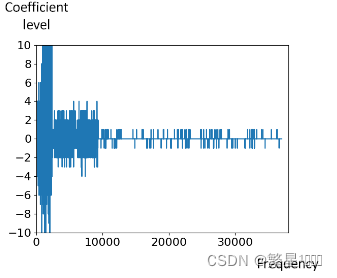
  • 对位移矢量进行小波变换，得到小波系数
  • 对小波系数进行量化得到系数层级，并分成块/子块
  • 小波系数表示成2值化的01串
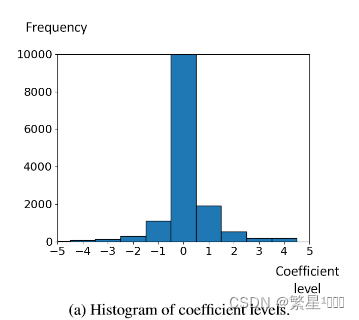
  • 因为系数层级取值0，1，2的频率最高，这几类用01组合的模式表示

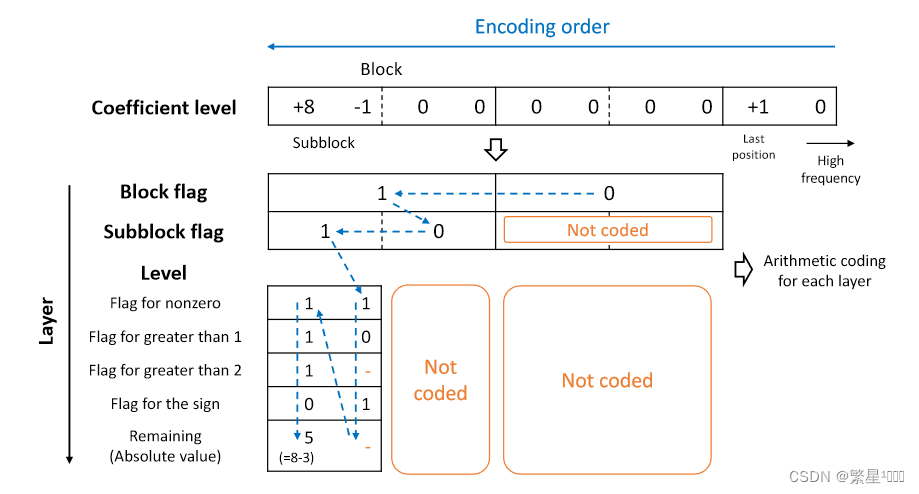
• 0,1,2的频次最多（不是-1，0，1最多吗）