关于数据集
2018年国际AIOps 由中国建设银行、清华大学以及必示科技公司联合举办,尽管已经过去了这么长时间,其提供的比赛数据依然被用于智能运维相关算法的研究。这里我们对此数据集做简单的分析,把一些常用的数据分析方法在这里进行略微地概述。
数据集下载地址:https://smileyan.lanzoul.com/ixpcU03lp97g
内容概述
接下来的部分我按照自己的习惯,使用python代码对数据进行简单的处理分析,不牵扯到具体论文的复现。
1. 加载数据
下载解压后,可以得到两个文件,即
- phase2_train.csv
- phase2_ground_truth.hdf
对于两种类型文件读取方法不同,代码如下:
import pandas as pd
df_train = pd.read_csv("data/phase2_train.csv")
print(df_train.head(5))
df_test = pd.read_hdf("data/phase2_ground_truth.hdf")
df_test["KPI ID"] = df_test["KPI ID"].astype(str)
print(df_test.head(5))
如下图所示:
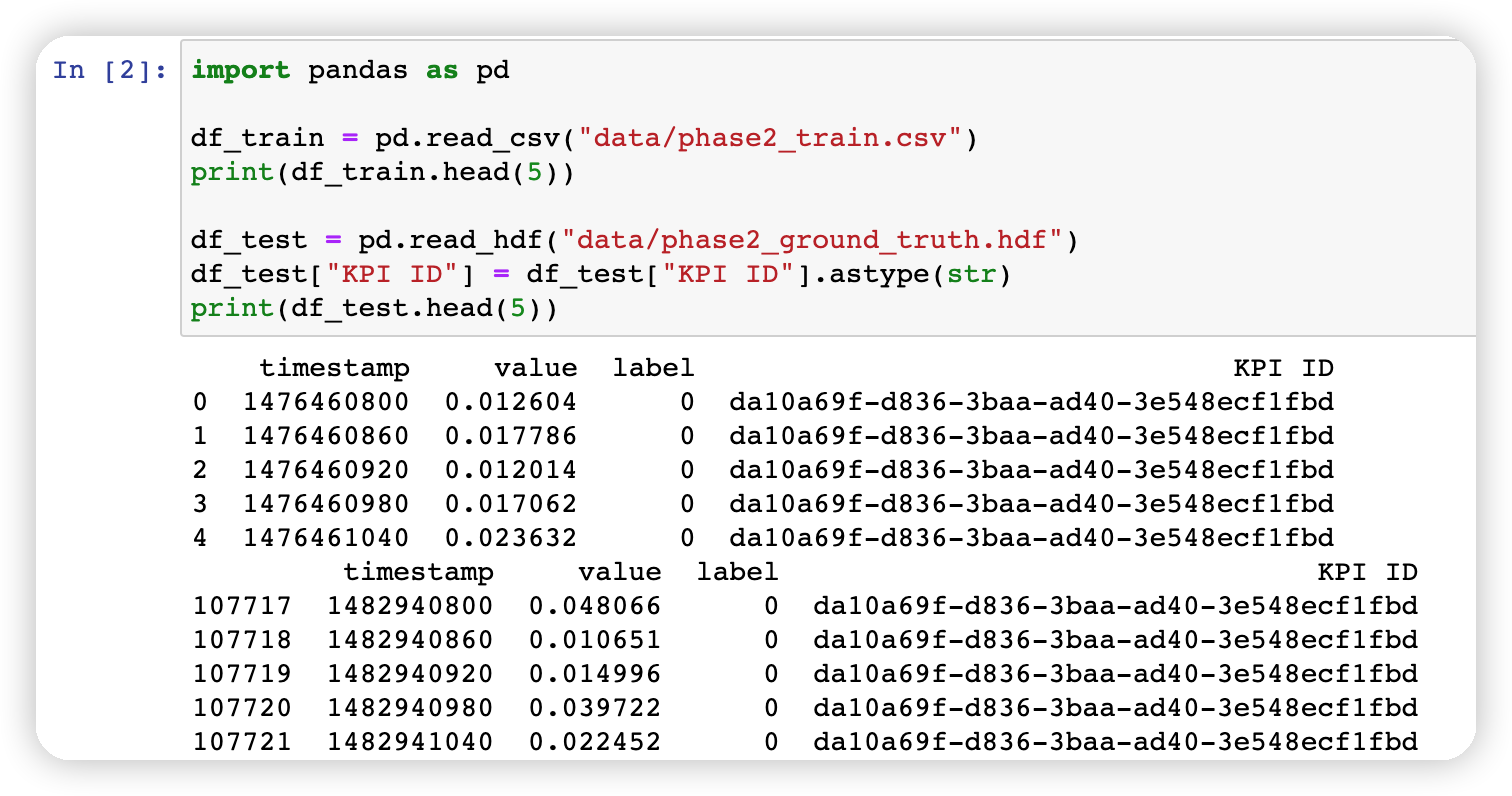
2. 使用 pd.groupby 拆分成多个 kpi
以训练集为例,这里先将整个df拆分成多个 DataFrame,以便于分别对不同的KPI进行分析。
首先统计一下总共多少种 KPI
df_train["KPI ID"].unique()
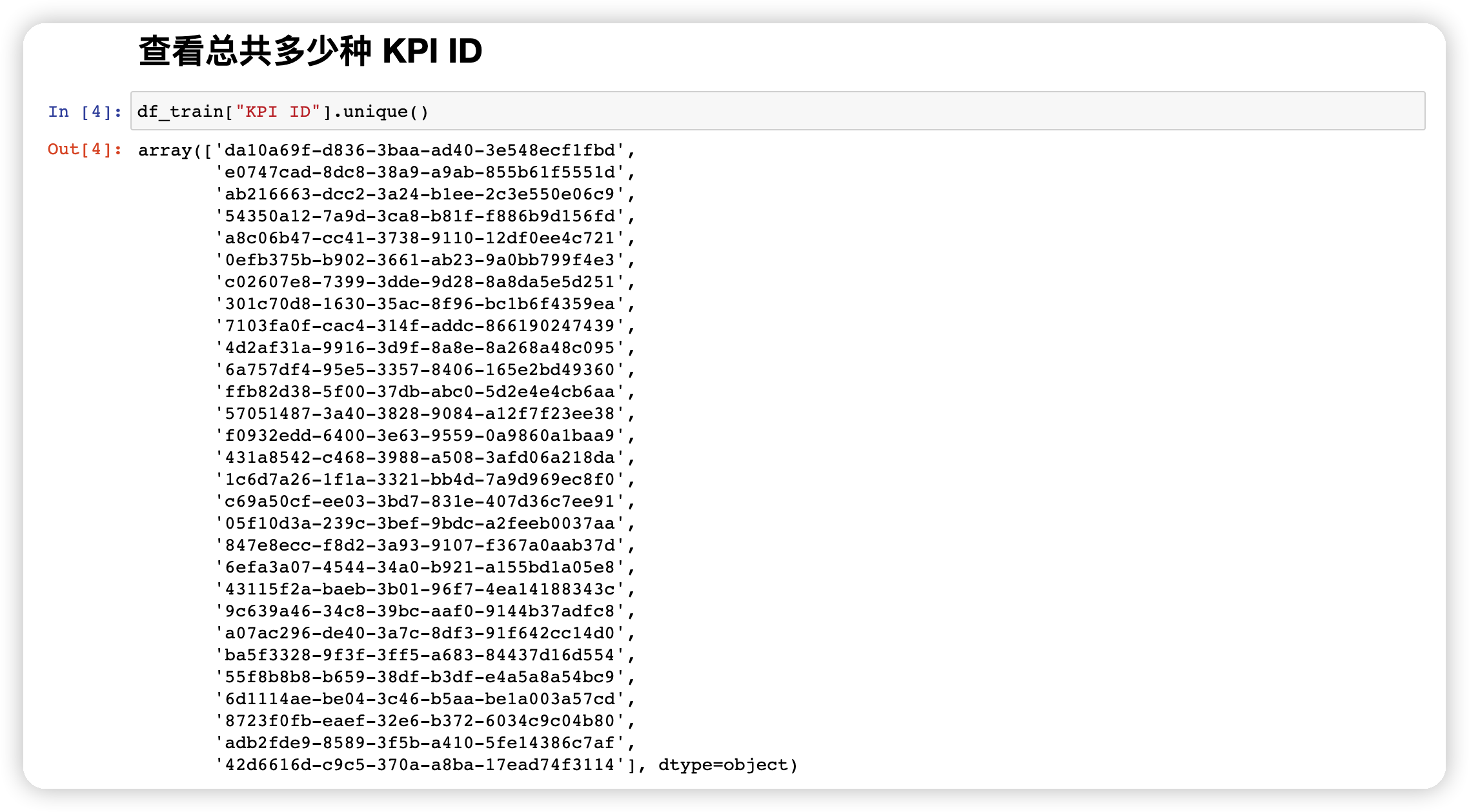
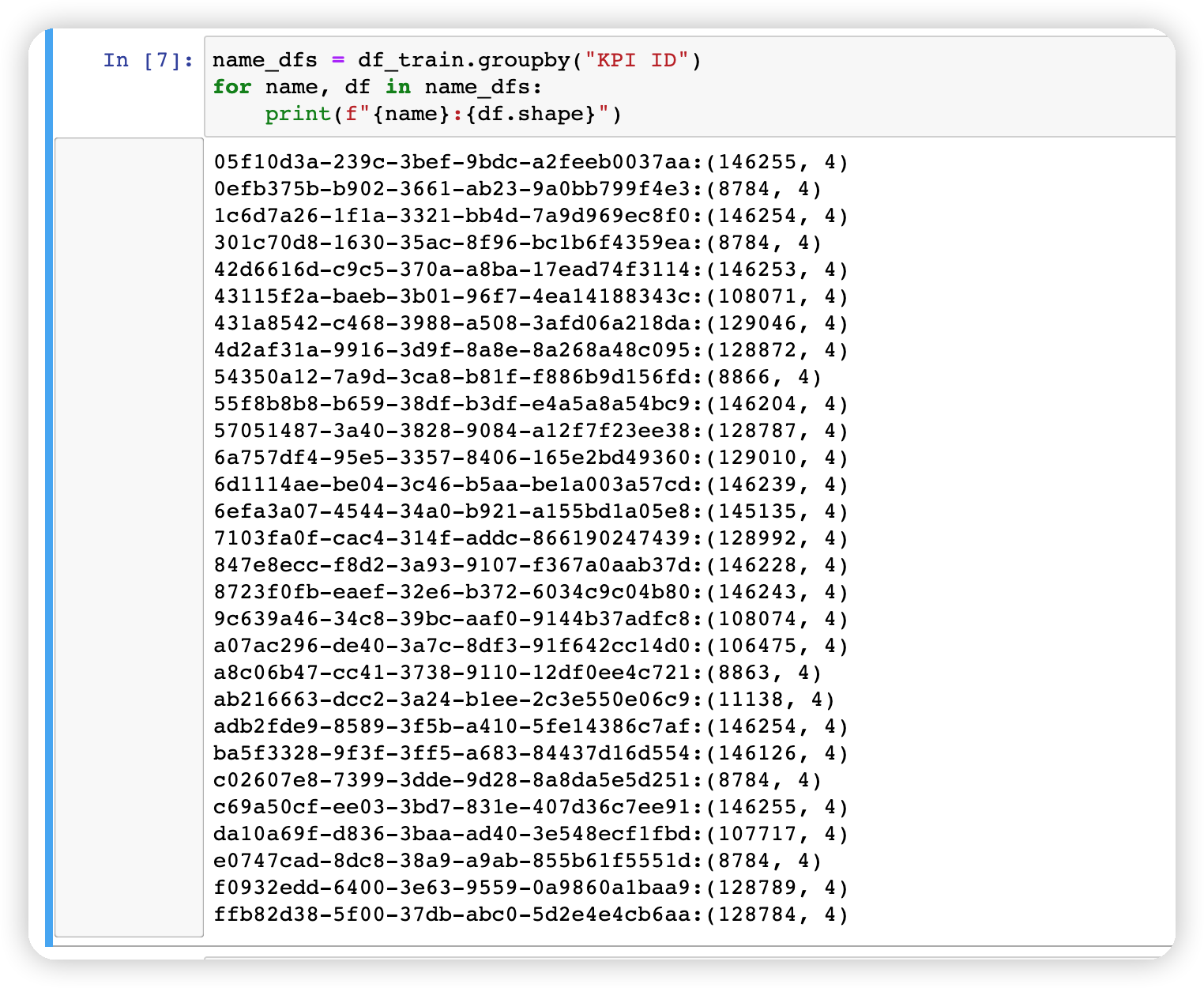
接着使用groupby收集每个指标,组成数组,并分析一下每个DataFrame 的shape。
name_dfs = df_train.groupby("KPI ID")
for name, df in name_dfs:
print(f"{name}:{df.shape}")
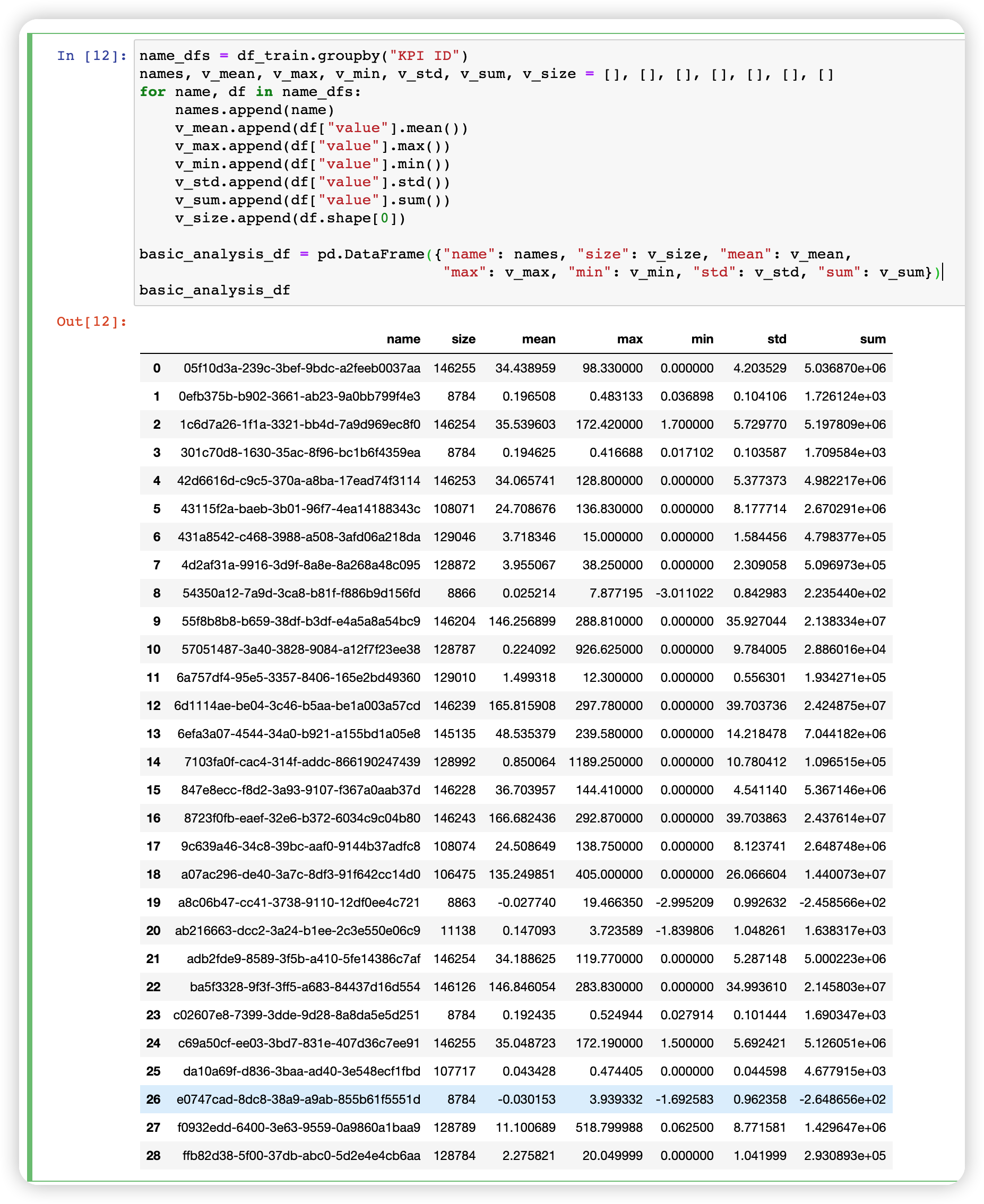
3. 其他基本特征
包括最大值最小值等等。
name_dfs = df_train.groupby("KPI ID")
names, v_mean, v_max, v_min, v_std, v_sum, v_size = [], [], [], [], [], [], []
for name, df in name_dfs:
names.append(name)
v_mean.append(df["value"].mean())
v_max.append(df["value"].max())
v_min.append(df["value"].min())
v_std.append(df["value"].std())
v_sum.append(df["value"].sum())
v_size.append(df.shape[0])
basic_analysis_df = pd.DataFrame({"name": names, "size": v_size, "mean": v_mean,
"max": v_max, "min": v_min, "std": v_std, "sum": v_sum})
basic_analysis_df
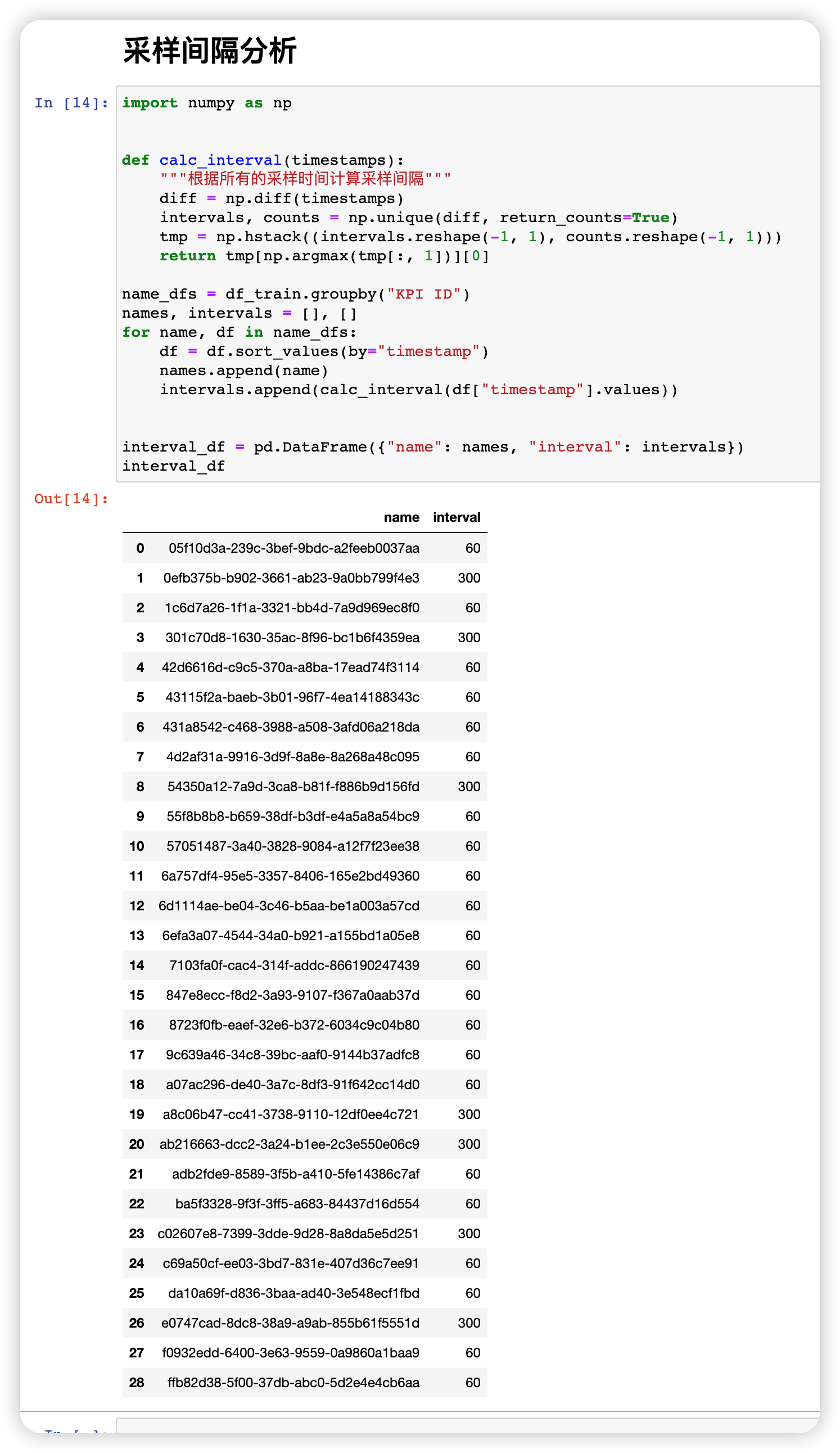
4. 分析采样间隔
不同的指标可能存在不同的缺失情况,但是一般情况下我们认为在所有的间隔中,占比最大的间隔为期望的采样间隔。比如说总共101个采样点,排序后计算它们的采样间隔,得到 1 分钟采样间隔共 80次,2分钟采样间隔20次,所以我们认为1分钟的采样间隔为最接近真实情况的采样间隔。
import numpy as np
def calc_interval(timestamps):
"""根据所有的采样时间计算采样间隔"""
diff = np.diff(timestamps)
intervals, counts = np.unique(diff, return_counts=True)
tmp = np.hstack((intervals.reshape(-1, 1), counts.reshape(-1, 1)))
return tmp[np.argmax(tmp[:, 1])][0]
name_dfs = df_train.groupby("KPI ID")
names, intervals = [], []
for name, df in name_dfs:
df = df.sort_values(by="timestamp")
names.append(name)
intervals.append(calc_interval(df["timestamp"].values))
interval_df = pd.DataFrame({"name": names, "interval": intervals})
interval_df
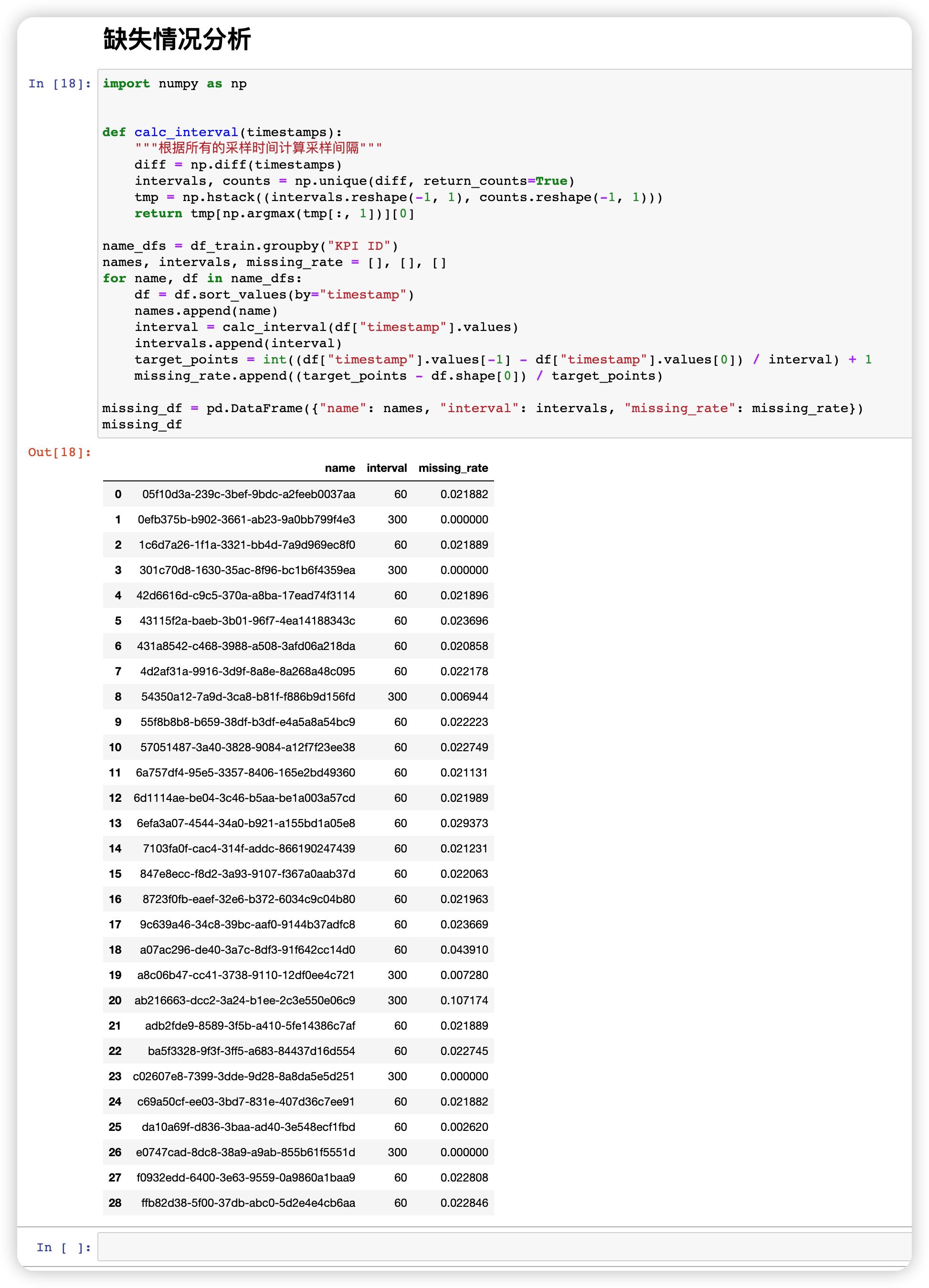
5. 缺失情况分析
计算得到采样间隔以后,即可分析数据缺失情况,方法也非常简单。
import numpy as np
def calc_interval(timestamps):
"""根据所有的采样时间计算采样间隔"""
diff = np.diff(timestamps)
intervals, counts = np.unique(diff, return_counts=True)
tmp = np.hstack((intervals.reshape(-1, 1), counts.reshape(-1, 1)))
return tmp[np.argmax(tmp[:, 1])][0]
name_dfs = df_train.groupby("KPI ID")
names, intervals, missing_rate = [], [], []
for name, df in name_dfs:
df = df.sort_values(by="timestamp")
names.append(name)
interval = calc_interval(df["timestamp"].values)
intervals.append(interval)
target_points = int((df["timestamp"].values[-1] - df["timestamp"].values[0]) / interval) + 1
missing_rate.append((target_points - df.shape[0]) / target_points)
missing_df = pd.DataFrame({"name": names, "interval": intervals, "missing_rate": missing_rate})
missing_df
6. 填充缺失值
为了接下来的分析工作需要,我们可能需要填充缺失值。这里采样最简单可靠的 “线性插值填充” 方法。不同情况下需要进行调整而进行填充,一般情况下如果不存在连续大段缺失的话,线性插值填充是可靠的。
总体过程可以概述为:
- 通过时间戳和采样间隔计算下一个点的时间戳;
- 判断下一个点的时间戳是否缺失,如果缺失则填充 np.nan;
- 使用 pandas 的工具进行线性填充。
def fill_missing_points(tv_df, interval):
"""填充缺失值"""
timestamps, values = tv_df["timestamp"].values, tv_df["value"].values
start = timestamps[0]
f_t, f_v = [], []
index = 0
while start <= timestamps[-1]:
if start == timestamps[index]:
f_t.append(start)
f_v.append(values[index])
index += 1
else:
f_t.append(start)
f_v.append(np.nan)
start += interval
r_df = pd.DataFrame({"timestamp": f_t, "value": f_v})
r_df["value"] = r_df["value"].interpolate()
return r_df
7. 使用 3-sigma 方法去除可能存在的异常值
3-sigma 也是一种光滑处理的方法,即计算原数据的标准差 σ \sigma σ 以及均值 μ \mu μ,对于原数据中每一个点 x x x 进行考察:
- 如果 x ∈ [ μ − 3 ∗ σ , μ + 3 ∗ σ ] x \in [\mu - 3 * \sigma, \mu + 3 * \sigma] x∈[μ−3∗σ,μ+3∗σ],则保留该点数据 x x x;
- 其他情况,去除这个点,以 μ − 3 ∗ σ \mu - 3 * \sigma μ−3∗σ 或者 μ + 3 ∗ σ \mu + 3*\sigma μ+3∗σ 进行填充。
def smooth_values(values, p=3):
"""平滑处理"""
mean, std = np.mean(values), np.std(values)
lower, upper = mean - p * std, mean + p * std
results = []
for value in values:
if lower <= value <= upper:
results.append(value)
else:
if value < lower:
results.append(lower)
elif value > upper:
results.append(upper)
return results
8. 周期类型分析
周期类型分析需要根据实际偏好进行调整,比如在特定场景中,只存在 “天周期” 、“周周期” 以及 “无周期” 三种情况,但是其他场景中可能存在 “月周期” 的情况等等。
这里我们使用 “相关系数” 来计算数据的周期类型,基本的原理是:分别对数据进行切块,分割成N个时间片段,然后计算相邻两个时间片段之间的相关系数,最终以所有的相关系数的均值作为最终的结果。
周期类型判断建立在需要推断采样间隔、完成缺失值填充、完成光滑处理的基础上。
def extract_seasonality(values, interval, t_w = 1.0, t_d = 1.0, t_season = 0.6):
"""提取周期类型
其中 t_w, t_d 分别代表周周期可能性系数、天周期可能性系数
t_season 表示具有周期性的最低相关系数
"""
s_values = smooth_values(values)
points_per_day = int(60 * 60 * 24 / interval)
points_per_week = points_per_day * 7
if len(values) < points_per_day:
return "NON"
p_w = calc_spearmanr(s_values, points_per_week)
p_d = calc_spearmanr(s_values, points_per_day)
if p_w < t_season and p_d < t_season:
return "NON"
if p_w * t_w >= p_d * t_d:
return "WEEK"
if p_w * t_w < p_d * t_d:
return "DAY"
return "NON"
有待补充
以上内容为常见的一些特征提取方法,在实际应用中一般会根据业务逻辑、实际数据场景进行调整。但总体而言大体如此,还有更多内容今后还会补充发布。
Smileyan
2023.09.24 19:00