一、一维差分

差分就是前缀和的逆运算,如果你不懂什么是前缀和,看这里->前缀和详解

数组a：a[1], a[2], a[3], a[n]
数组b ： b[1] ,b[2] , b[3], b[i]
使得 a数组是b数组的前缀和,b数组是a数组的差分
a[i] = b[1] + b[2] + …+ b[i]

数字来看的话就是这样的:
a数组1 3 7 5 2
b数组1 2 4 -2 -3
Sumb数组1 1+2 1+2+4 1+2+4-2 1+2+4-2-3
----------也就是1 3 7 5 2跟原数组还是相同的
a是b的前缀和,b是a的差分.

那么,问题来了,差分有什么用呢?

当你把一个区间[L,R]的数都加上或减去某一个数x的时候,该怎末做呢?第一时间想到的肯定是暴力做法,输入LR区间,然后for循环,直接暴力解决,确实暴力解法能解决很多事情,但是时间复杂度很高,为O(n),如果想进行m次区间加上或减去x的操作呢?每次都遍历LR区间,那么时间复杂度就更高了O(n*m).这个时候,就有人对其优化,想出来了一种名为差分的解法,差分解法呢,有一个公式:[L,R] + X <==>差分数组[L] + X,差分数组[R+1] - X;
那么,这个公式是怎么来的?
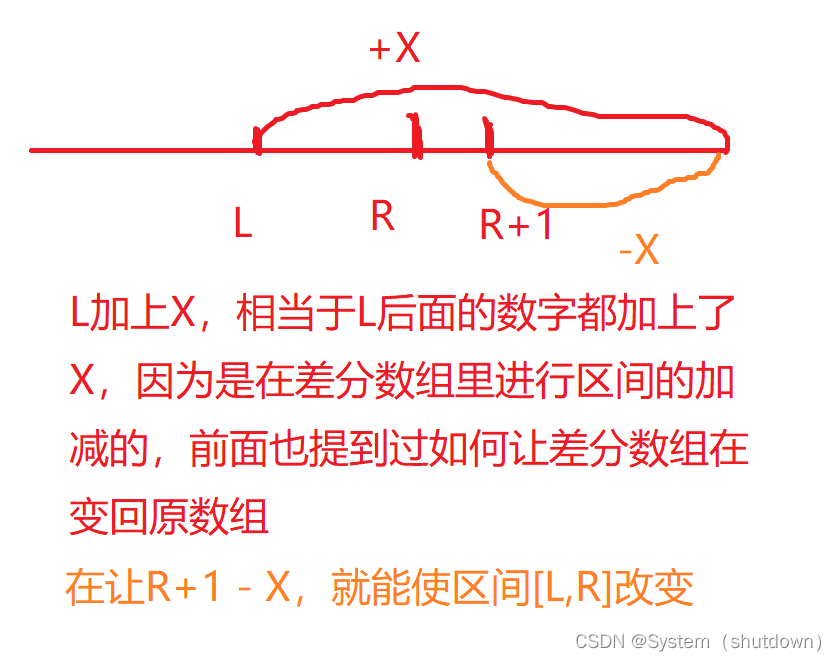
在这里插入图片描述
下面看一道例题:

输入一个长度为 n 的整数序列。

接下来输入 m 个操作，每个操作包含三个整数 l,r,c，表示将序列中 [l,r] 之间的每个数加上 c。

请你输出进行完所有操作后的序列。

输入格式

第一行包含两个整数 n 和 m。

第二行包含 n 个整数，表示整数序列。

接下来 m 行，每行包含三个整数 l，r，c，表示一个操作。

输出格式

共一行，包含 n 个整数，表示最终序列。

数据范围

1≤n,m≤100000, 1≤l≤r≤n, −1000≤c≤1000, −1000≤整数序列中元素的值≤1000

输入样例：

—6 3
—1 2 2 1 2 1
—1 3 1
—3 5 1
—1 6 1

输出样例：

3 4 5 3 4 2

1.先输入数组

	for (int i = 1; i <= n; i++)
	{
		cin >> a[i];
	}

然后把原数组a,变成差分数组b

	void insert(int l, int r, int c)
	{
		b[l] += c;
		b[r + 1] -= c;
	}


	for (int i = 1; i <= n; i++)
	{
		insert(i, i, a[i]);
	}

对差分数组进行m次操作

	while (m--)
	{
		int l, r, c;
		cin >> l >> r >> c;
		insert(l, r, c);
	}

最后,将差分数组变回原数组

	for (int i = 1; i <= n; i++)
	{
		b[i] += b[i - 1];
		cout << b[i] << ' ';
	}

总代码

#include <iostream>

using namespace std;

const int N = 1e6 + 10;

int a[N];

int b[N];

void insert(int l, int r, int c)
{
	b[l] += c;
	b[r + 1] -= c;
}

int main()
{
	int n, m;
	cin >> n >> m;
	for (int i = 1; i <= n; i++)
	{
		cin >> a[i];
	}

	for (int i = 1; i <= n; i++)
	{
		insert(i, i, a[i]);
	}

	while (m--)
	{
		int l, r, c;
		cin >> l >> r >> c;
		insert(l, r, c);
	}

	for (int i = 1; i <= n; i++)
	{
		b[i] += b[i - 1];
		cout << b[i] << ' ';
	}


	return 0;
}

题目来源acwing799

二、二维差分

二维差分也就是二维前缀和的逆运算,其构造差分的过程和构造一维差分的过程差不多类似.在这里主要说一下构造过程:

void insert(int x1, int y1, int x2, int y2, int c)
{
    b[x1][y1] += c;
    b[x2 + 1][y1] -= c;
    b[x1][y2 + 1] -= c;
    b[x2 + 1][y2 + 1] += c;
}

标红区区域便是x1,y1进行区间加或减操作的区域

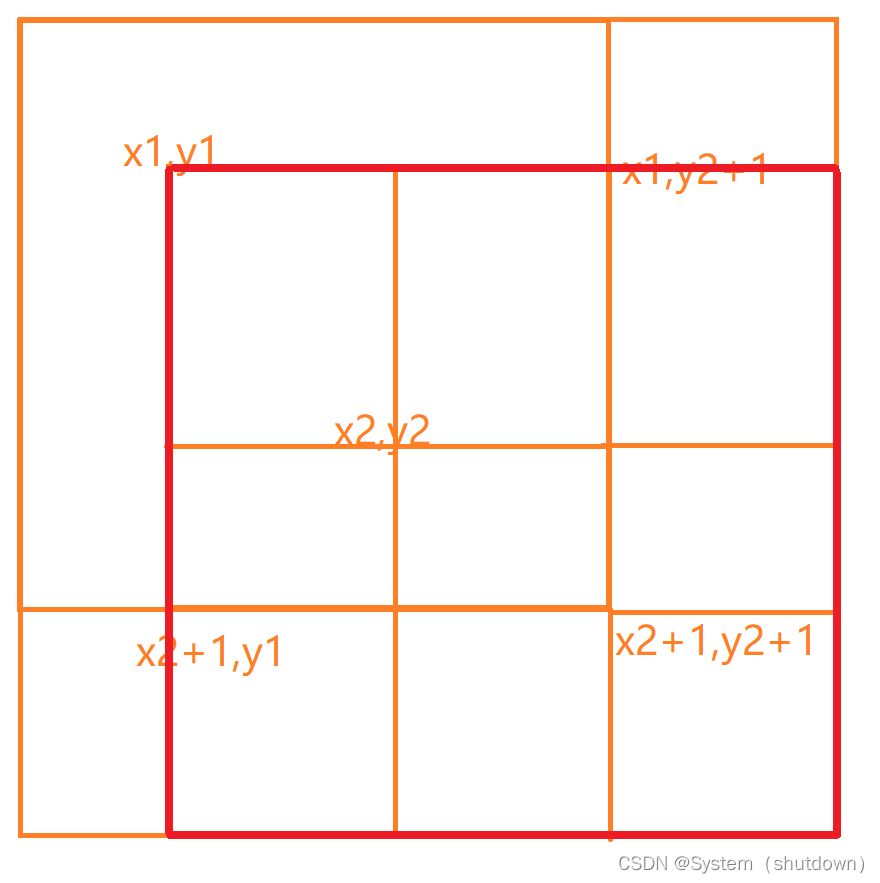
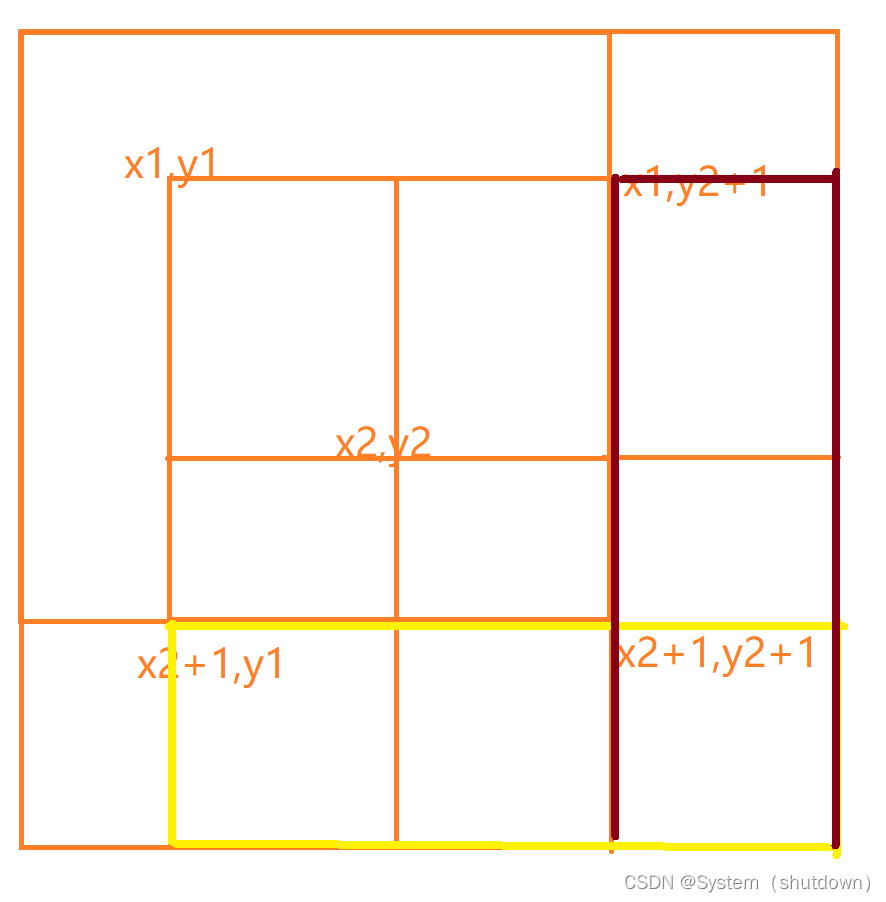
在这里插入图片描述

黄色和咖啡色区域便是x2+1,y1和x1,y2+1的区间,而有x2+1,y2+1的区间是重叠的部分,也就是说,在 b[x2 + 1][y1] -= c; b[x1][y2 + 1] -= c;这两部中,x2+1,y2+1被多减了一次,所以要把这部分还回去,也就是这一步 b[x2 + 1][y2 + 1] += c;

在这里插入图片描述

下面看一到例题

输入一个 n 行 m 列的整数矩阵，再输入 q 个操作，每个操作包含五个整数 x1,y1,x2,y2,c，其中 (x1,y1) 和(x2,y2) 表示一个子矩阵的左上角坐标和右下角坐标。

每个操作都要将选中的子矩阵中的每个元素的值加上 c。

请你将进行完所有操作后的矩阵输出。

输入格式

第一行包含整数 n,m,q。

接下来 n 行，每行包含 m 个整数，表示整数矩阵。

接下来 q 行，每行包含 5 个整数 x1,y1,x2,y2,c，表示一个操作。

输出格式

共 n 行，每行 m 个整数，表示所有操作进行完毕后的最终矩阵。

数据范围

1≤n,m≤1000,
1≤q≤100000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤c≤1000,
−1000≤矩阵内元素的值≤1000

输入样例：

3 4 3

1 2 2 1

3 2 2 1

1 1 1 1

1 1 2 2 1

1 3 2 3 2

3 1 3 4 1

输出样例：

2 3 4 1

4 3 4 1

2 2 2 2

代码

#include <iostream>

using namespace std;

const int N = 1010;

int n, m, q;
int a[N][N], b[N][N];

void insert(int x1, int y1, int x2, int y2, int c)
{
    b[x1][y1] += c;
    b[x2 + 1][y1] -= c;
    b[x1][y2 + 1] -= c;
    b[x2 + 1][y2 + 1] += c;
}

int main()
{
    scanf("%d%d%d", &n, &m, &q);

    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            scanf("%d", &a[i][j]);

    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            insert(i, j, i, j, a[i][j]);

    while (q--)
    {
        int x1, y1, x2, y2, c;
        cin >> x1 >> y1 >> x2 >> y2 >> c;
        insert(x1, y1, x2, y2, c);
    }

    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];

    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= m; j++) printf("%d ", b[i][j]);
        puts("");
    }

    return 0;
}