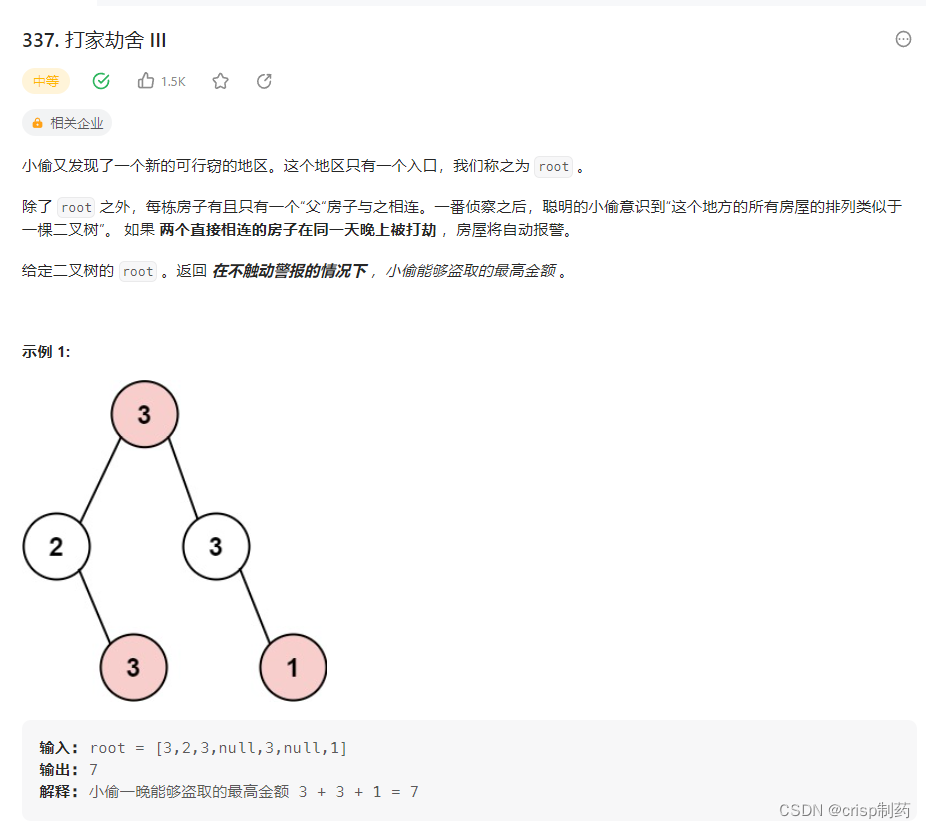
public class Solution {

    // 树的后序遍历

    public int rob(TreeNode root) {
        int[] res = dfs(root);
        return Math.max(res[0], res[1]);
    }

    private int[] dfs(TreeNode node) {
        if (node == null) {
            return new int[]{0, 0};
        }

        // 分类讨论的标准是：当前结点偷或者不偷
        // 由于需要后序遍历，所以先计算左右子结点，然后计算当前结点的状态值
        int[] left = dfs(node.left);
        int[] right = dfs(node.right);

        // dp[0]：以当前 node 为根结点的子树能够偷取的最大价值，规定 node 结点不偷
        // dp[1]：以当前 node 为根结点的子树能够偷取的最大价值，规定 node 结点偷
        int[] dp = new int[2];

        dp[0] = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);
        dp[1] = node.val + left[0] + right[0];
        return dp;
    }
}

dp[i][0]：规定了今天不持股，有以下两种情况：
昨天不持股，今天什么都不做；
昨天持股，今天卖出股票（现金数增加），
dp[i][1]：规定了今天持股，有以下两种情况：
昨天持股，今天什么都不做（现金数与昨天一样）；
昨天不持股，今天买入股票（注意：只允许交易一次，因此手上的现金数就是当天的股价的相反数）。

class Solution {
    public int maxProfit(int[] prices) {
         int len = prices.length;
        // 特殊判断
        if (len < 2) {
            return 0;
        }
        int[][] dp = new int[len][2];

        // dp[i][0] 下标为 i 这天结束的时候，不持股，手上拥有的现金数
        // dp[i][1] 下标为 i 这天结束的时候，持股，手上拥有的现金数

        // 初始化：不持股显然为 0，持股就需要减去第 1 天（下标为 0）的股价
        dp[0][0] = 0;
        dp[0][1] = -prices[0];

        // 从第 2 天开始遍历
        for (int i = 1; i < len; i++) {
        	// 不持股的话就可能前一天也不持股直接转移状态，或者是今天才，所以就前一天持股的状态加上price【i】
            dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
            dp[i][1] = Math.max(dp[i - 1][1], -prices[i]);
        }
        return dp[len - 1][0];

    }
}

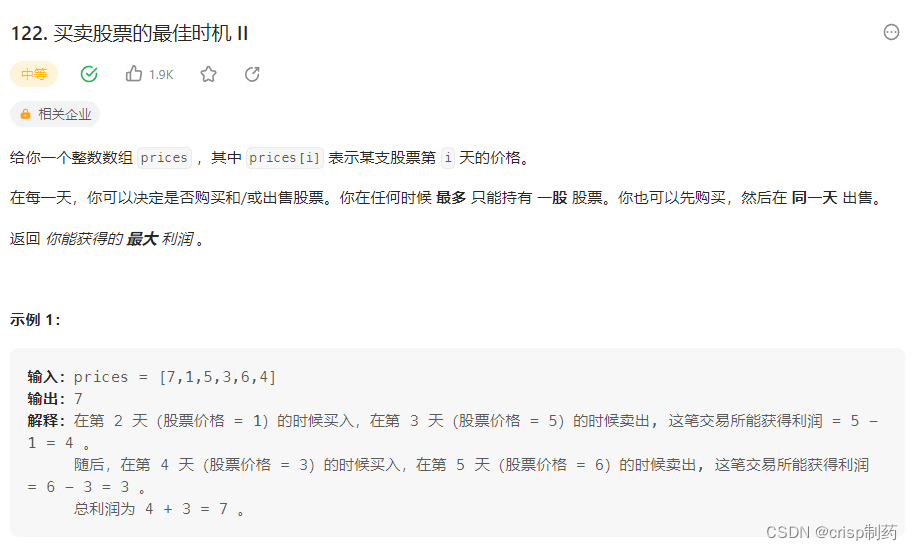
这题的交易次数变成了无数次，其实和上题类似，注意状态转移方程的修改就好。

class Solution {
    public int maxProfit(int[] prices) {
        if(prices.length == 0 || prices == null){
            return 0;
        }
        int length = prices.length;
        int [][] dp = new int [length][2];
        dp[0][0]=0;
        dp[0][1]=-prices[0];
        for(int i=1;i<length;i++){
            dp[i][0]=Math.max(dp[i-1][0],dp[i-1][1]+prices[i]);
            dp[i][1]=Math.max(dp[i-1][1],dp[i-1][0]-prices[i]);
        }
        return dp[length-1][0];
    }
}

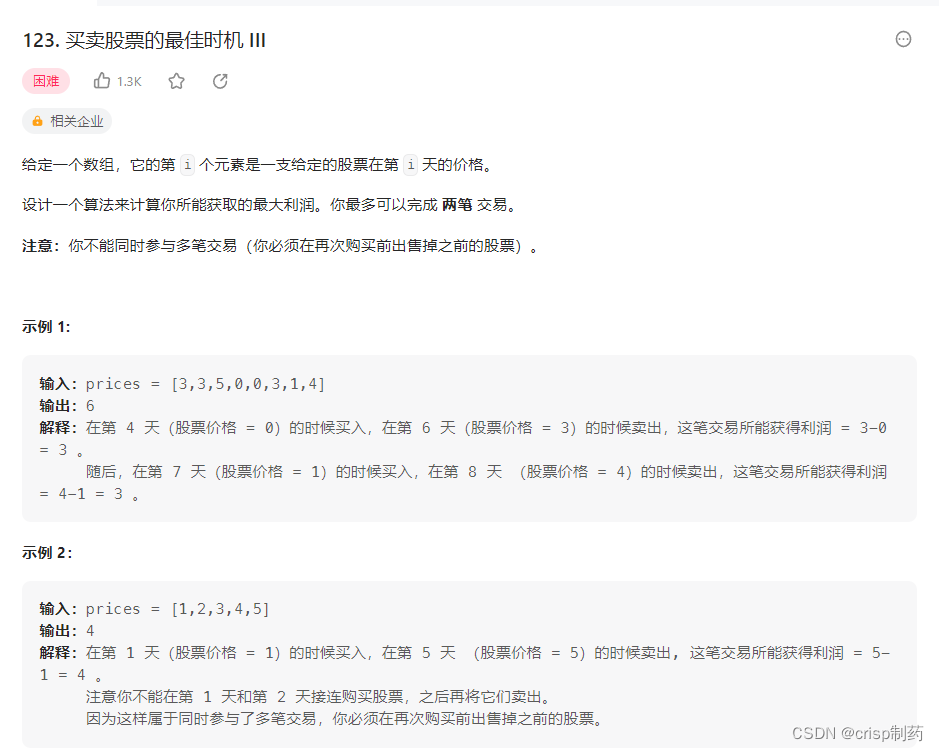
情况三和情况一相似，区别之处是，对于情况三，每天有四个未知变量：T[i][1][0]、T[i][1][1]、T[i][2][0]、T[i][2][1]，中间那一维是表示交易第几次，因为这题是要交易两次

public class Solution {

    public int maxProfit(int[] prices) {
        int len = prices.length;
        if (len < 2) {
            return 0;
        }

        // 第 2 维的 0 没有意义，1 表示交易进行了 1 次，2 表示交易进行了 2 次
        // 为了使得第 2 维的数值 1 和 2 有意义，这里将第 2 维的长度设置为 3
        int[][][] dp = new int[len][3][2];

        // 理解如下初始化
        // 第 3 维规定了必须持股，因此是 -prices[0]
        dp[0][1][1] = -prices[0];
        // 还没发生的交易，必须由前面状态转移得到，所以持股的时候应该初始化为负无穷
        dp[0][2][1] = Integer.MIN_VALUE;

        for (int i = 1; i < len; i++) {
            // 转移顺序先持股，再卖出
            dp[i][1][1] = Math.max(dp[i - 1][1][1], -prices[i]) ;
            dp[i][1][0] = Math.max(dp[i - 1][1][0], dp[i - 1][1][1] + prices[i]);
            dp[i][2][1] = Math.max(dp[i - 1][2][1], dp[i - 1][1][0] - prices[i]);
            dp[i][2][0] = Math.max(dp[i - 1][2][0], dp[i - 1][2][1] + prices[i]);
        }
        //题目说的是最多可以买两次，不一定是一定要买两次，所以是从买1次和买2次中取最大值
        return Math.max(dp[len - 1][1][0], dp[len - 1][2][0]);
    }
}