矩阵的c++实现

news2025/2/22 12:20:25

在大学数学课程《线性代数》中，就有矩阵和行列式的出现，这篇文章主要讲矩阵在c++中的实现和一些用途（目前我知道的）

此篇文章只写c++的内容，不具体写到数学中矩阵的一些公式、性质。

本篇文章中一部分图片来自百度百科。

注：在编程中，习惯（不知道是不是只有我的习惯）写成n行m列矩阵，但在数学课本中，是m行n列的矩阵，不要搞混了

一、矩阵是什么

由 n×m 个数aij排成的n行m列的数表称为n行m列的矩阵，简称n×m矩阵。记作：

$A=\begin{bmatrix} a11,a12,a13,...,a1m \\ a21,a22,a23,...,a2m \\ a31,a32,a33,...,a3m \\ ...,...,...,...,... \\ an1,an2,an3,...,anm \end{bmatrix}$

第一次用公式不会用

二、构建一个矩阵

#include<bits/stdc++.h>
#define maxn 100 
using namespace std;
struct Matrix{
	int n,m;//n行m列矩阵 
	long long a[maxn][maxn];
	Matrix(){
		memset(a,0,sizeof a);
	}
	Matrix(int _n, int _m) {
        n=_n;
        m=_m;
        memset(a,0,sizeof a);
    }
    void scan(){
    	cin>>n>>m;
    	for(int i=0;i<n;i++){
    		for(int j=0;j<m;j++){
    			cin>>a[i][j];
			}
		}
	}
	void print(){
    	for(int i=0;i<n;i++){
    		for(int j=0;j<m;j++){
    			cout<<a[i][j]<<" ";
			}
			cout<<endl;
		}
	}
};
int main(){
	Matrix a;
	a.scan();
	a.print();
	return 0;
}

非常简单

三、矩阵的运算

1.加法

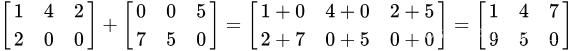
只有m和n都相同的矩阵才可以相加。

设C=A+B，则：

Cij=Aij+Bij

矩阵加法满足交换律和结合律：

A+B=B+A

A+(B+C)=(A+B)+C

代码：

Matrix pl(Matrix a,Matrix b){
	for(int i=0;i<a.n;i++){
		for(int j=0;j<a.m;j++){
			a.ma[i][j]+=b.ma[i][j];
		}
	}
	return a;
}
int main(){
	Matrix a,b;
	a.scan();
	b.scan();
	pl(a,b).print();
	return 0;
}

因为a会和矩阵里面的a长得很像，我就改了

2.数乘

就是将一个矩阵乘以一个数字

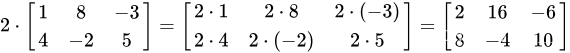
Matrix mul_num(Matrix a,int b){
	for(int i=0;i<a.n;i++){
		for(int j=0;j<a.m;j++){
			a.ma[i][j]*=b;
		}
	}
	return a;
}

满足以下定律：

结合律：a(bA)=(ab)A

交换律：aA=Aa

分配律：(a+b)A=aA+bA

(A+B)a=aA+aB

好了，新手期度过

3.矩阵乘法

当A*B时，必须满足A的n（列数）和B的m（行数）相同。当A为p*n矩阵，B为n*q矩阵时，C为p*q矩阵。

他的元素：

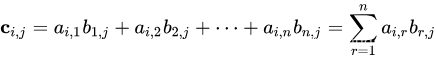
Matrix mul(Matrix a,Matrix b){
	Matrix res(a.n,b.m);
	for(int i=0;i<a.n;i++){
		for(int j=0;j<b.m;j++){
			for(int k=0;k<a.m;k++){
				res.ma[i][j]+=a.ma[i][k]*b.ma[k][j];
			}
		}
	}
	return res;
}

矩阵乘法满足的运算定律：

结合律：A(BC)=(AB)C

左分配律：C(A+B)=CA+CB

右分配律：(A+B)C=AC+BC

4.单位矩阵

我们都知道，1*a=a，那么如果我们要在矩阵中找到一个和1的性质一样的矩阵，要怎么做呢？？？

单位矩阵出场！

单位矩阵：一个n*n的矩阵，左下角到右下角都是1，其他都是0。

当n*m的矩阵乘以一个n*n的单位矩阵时，不会发生改变。

具体过程如下：

$\begin{bmatrix} 2,3\\ 5,6\\ 4,3 \end{bmatrix}\times \begin{bmatrix} 1 ,0 \\ 0,1 \end{bmatrix}=\begin{bmatrix} 2\times1+0,3\times1+0 \\ 5\times1+0,6\times1+0 \\ 4\times1+0,3\times1+0 \end{bmatrix}$

单位矩阵在快速幂中有用

5.矩阵快速幂

只有n*n矩阵才可以快速幂。

如何快速幂？？？

矩阵的快速幂和普通的不同，我们可以这样想：

A^7=A*A*A*A*A*A*A=(A*A)*(A*A)*A*A*A

说起来有些奇妙，但实际上就是个这样的过程：

Matrix mpow(Matrix a,int n){
	Matrix res(a.n,a.n);
	for(int i=0;i<res.n;i++)res.ma[i][i]=1;
    while(n!=0){
        if(n&1)res=mul(res,a);
        a=mul(a,a);
        n>>=1;
    }
    return res;
}

你可能看不懂，但如果我把他变成数字的快速幂，你就懂了。

int mpow(int a,int n){
	int res=1;//初始化
    while(n!=0){
        if(n&1)res=a*res;//统计多出来的a
        a=a*a;
        n>>=1;//就是除2
    }
    return res;
}

我们刚开始构建一个单位矩阵res，用他充当1的作用。

6.所有运算的代码

#include<bits/stdc++.h>
#define maxn 100 
using namespace std;
int mm;
struct Matrix{
	int n,m;
	long long ma[maxn][maxn];
	Matrix(){
		memset(ma,0,sizeof ma);
	}
	Matrix(int _n, int _m) {
        n=_n;
        m=_m;
        memset(ma,0,sizeof ma);
    }
    void scan(){
    	cin>>n>>m;
    	for(int i=0;i<n;i++){
    		for(int j=0;j<m;j++){
    			cin>>ma[i][j];
			}
		}
	}
	void print(){
    	for(int i=0;i<n;i++){
    		for(int j=0;j<m;j++){
    			cout<<ma[i][j]<<" ";
			}
			cout<<endl;
		}
	}
};
Matrix pl(Matrix a,Matrix b){
	for(int i=0;i<a.n;i++){
		for(int j=0;j<a.m;j++){
			a.ma[i][j]+=b.ma[i][j];
		}
	}
	return a;
}
Matrix mul_num(Matrix a,int b){
	for(int i=0;i<a.n;i++){
		for(int j=0;j<a.m;j++){
			a.ma[i][j]*=b;
		}
	}
	return a;
}
Matrix mul(Matrix a,Matrix b){
	Matrix res(a.n,b.m);
	for(int i=0;i<a.n;i++){
		for(int j=0;j<b.m;j++){
			for(int k=0;k<a.m;k++){
				res.ma[i][j]+=a.ma[i][k]*b.ma[k][j];
			}
		}
	}
	return res;
}
Matrix mpow(Matrix a,int n){
	Matrix res(a.n,a.n);
	for(int i=0;i<res.n;i++)res.ma[i][i]=1;
    while(n!=0){
        if(n&1)res=mul(res,a);
        a=mul(a,a);
        n>>=1;
    }
    return res;
}
int main(){
	return 0;
}

四、矩阵在编程中的运用

既然我们说了这么多，你可能会很疑惑：为什么我们要用到矩阵呢？编程中哪里需要用到矩阵呢？

我学矩阵时也这样，好像矩阵离我很远的样子。

那么我们来看几道例题：

1.洛谷P1962斐波那契数列

这道题用矩阵解很简单，有两种相似的做法。

第一种做法

我们都知道，斐波那契数列的式子是：

$F_{n}=F_{n-1}+F_{n-2}$

那我们考虑行矩阵

$\begin{bmatrix} F_{n},F_{n-1} \end{bmatrix} =\begin{bmatrix} F_{n-1},F_{n-2}\end{bmatrix}\times base$

那我们就要考虑base是什么

分解：

$[F_{n},F_{n-1}]=[F_{n-1}+F_{n-1},F_{n-1}]$

$=[1\times F_{n-1}+1\times F_{n-2},1\times F_{n-1}+0\times F_{n-2}]$

$=[F_{n-1},F_{n-2}]\times \begin{bmatrix} 1,1\\ 1,0\\ \end{bmatrix}$

这不就巧了吗，刚好就出现了n-1项和n-2项,那么base就是这个1110了

根据左分配律，可以得出，我们不断递推，就相当于

$[1,1]\times base^{n-2}$

多思考一下就可以得出了

那么，最后只要输出就行了

代码如下

#include<bits/stdc++.h>
#define maxn 100 
using namespace std;
int mm;
struct Matrix{
	int n,m;
	long long ma[maxn][maxn];
	Matrix(){
		memset(ma,0,sizeof ma);
	}
	Matrix(int _n, int _m) {
        n=_n;
        m=_m;
        memset(ma,0,sizeof ma);
    }
    void scan(){
    	cin>>n>>m;
    	for(int i=0;i<n;i++){
    		for(int j=0;j<m;j++){
    			cin>>ma[i][j];
			}
		}
	}
	void print(){
    	for(int i=0;i<n;i++){
    		for(int j=0;j<m;j++){
    			cout<<ma[i][j]<<" ";
			}
			cout<<endl;
		}
	}
};
Matrix pl(Matrix a,Matrix b){
	for(int i=0;i<a.n;i++){
		for(int j=0;j<a.m;j++){
			a.ma[i][j]+=b.ma[i][j];
		}
	}
	return a;
}
Matrix mul_num(Matrix a,int b){
	for(int i=0;i<a.n;i++){
		for(int j=0;j<a.m;j++){
			a.ma[i][j]*=b;
		}
	}
	return a;
}
Matrix mul(Matrix a,Matrix b){
	Matrix res(a.n,b.m);
	for(int i=0;i<a.n;i++){
		for(int j=0;j<b.m;j++){
			for(int k=0;k<a.m;k++){
				res.ma[i][j]+=a.ma[i][k]*b.ma[k][j];
			}
		}
	}
	return res;
}
Matrix mpow(Matrix a,int n){
	Matrix res(a.n,a.n);
	for(int i=0;i<res.n;i++)res.ma[i][i]=1;
    while(n!=0){
        if(n&1)res=mul(res,a);
        a=mul(a,a);
        n>>=1;
    }
    return res;
}
int main(){
	return 0;
}

第二种做法

我们换成竖的：

$\begin{bmatrix} F_{n}\\ F_{n-1}\\ \end{bmatrix}$

理论差不多，不多说了。~~不然又浪费我的手和时间~~

应该都会了吧，自己推吧，直接上代码（因为是上课写的，格式有些不一样）

#include <bits/stdc++.h>
using namespace std;
const int maxn = 100 + 10;
int mod;
typedef long long ll;
struct Matrix {
    int n, m;
    long long a[maxn][maxn];
    Matrix() { memset(a, 0, sizeof a); }
    Matrix(int _n, int _m) {
        n = _n;
        m = _m;
        memset(a, 0, sizeof a);
    }
};
Matrix mul(Matrix &a, Matrix &b) {
    Matrix res(a.n, b.m);
    for(int i=0;i<a.n;i++)
        for(int j=0;j<b.m;j++)
            for(int k=0;k<a.m;k++)
                res.a[i][j]+=a.a[i][k]*b.a[k][j]%mod;
    return res;
}
Matrix Pow(Matrix &base, ll n) {
    Matrix res(base.n, base.n);
    for(int i=0;i<res.n;i++)res.a[i][i]=1;
    while(n!=0){
        if(n&1)res=mul(res,base);
        base=mul(base,base);
        n>>=1;
    }
    return res;
}
int main() {
    freopen("Fibonacci.in", "r", stdin);
    freopen("Fibonacci.out", "w", stdout);
    ll n;
    scanf("%lld%d", &n, &mod);
    if (n == 1 || n == 2) return 0 * puts("1");
    Matrix F(1,2);
    F.a[0][0]=1;
    Matrix A(2,2);
    A.a[0][0]=1;
    A.a[0][1]=1;
    A.a[1][0]=1;
    A.a[1][1]=0;
    A=Pow(A,n-1);
    F=mul(F,A);
    cout<<F.a[0][0];
    return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1035207.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！