个人主页：Lei宝啊

愿所有美好如期而遇

---

前言： 

在堆这一节中，孩子和其父节点有如下关系：

左孩子：left_child = parent * 2 + 1;

右孩子：right_child = parent * 2 + 2;

父节点在计算时，因为兄弟节点的父母都相同，所以对兄弟节点来说;

parent = (left_child - 1)/2;  或者

parent = (right_child - 2)/2;

但我们会发现，右孩子按照左孩子计算的方法仍然能够找到父母，所以我们在找孩子的父母时，都按左孩子那样算了。

---

堆向上调整：

在数组尾插入数字后，要调整，但要保证前面的数据是一个堆

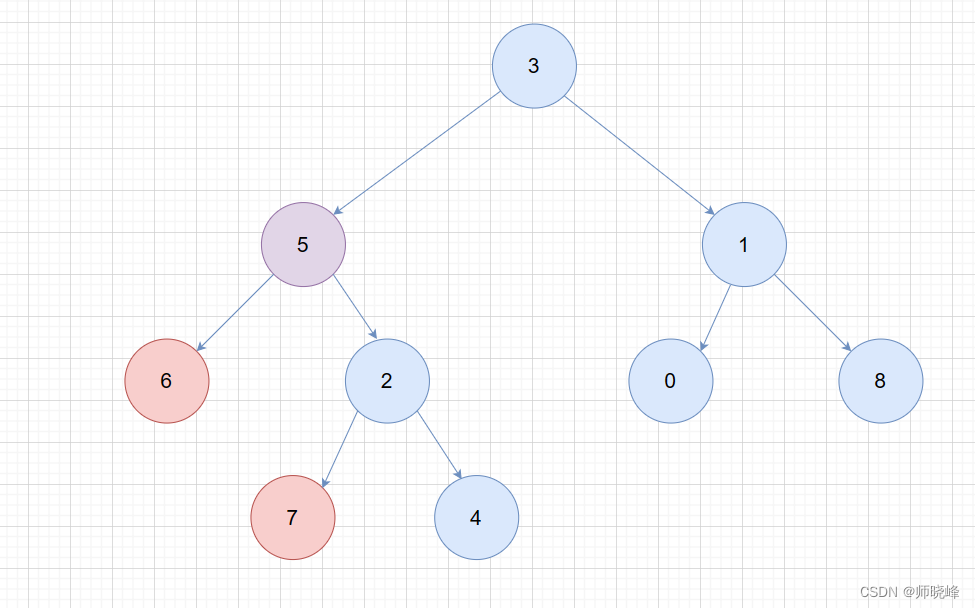
图解：

--->假设我们建小堆<---

依次类推节点

代码：

//堆向上调整，调整一轮，建堆就循环插入去建
void Ajustup(Heaptype* a, int child)
{
 
	int parent = (child - 1) / 2;
 
	//当child == 0 的时候，parent也为0
	while (child > 0)
	{
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
		
}

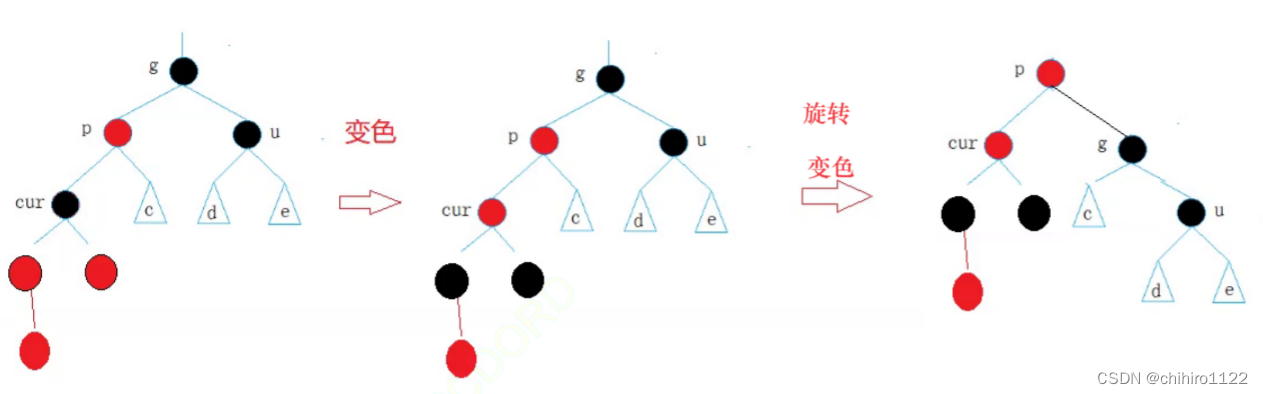
堆向下调整：

在向下调整时要保证其左右子树都为堆，才可继续调整

图解：

代码：

//堆向下调整
void AjustDown(Heaptype* a, int n, int parent)
{
	
	//从叶子节点开始
	int child = parent * 2 + 1;
 
	while (child < n)
	{
		//找出最小孩子
		if (child + 1 < n && a[child] > a[child + 1])
		{
			child++;
		}
		else
		{
			if (a[parent] > a[child])
			{
				Swap(&a[child], &a[parent]);
				parent = child;
				child = parent * 2 + 1;
			}	
			else
			{
				break;
			}
		}
	}
 
}

堆向上调整建堆：

思路及代码：

插入建堆，在一个堆后插入数据，直接调整一次就可以，代码如下：（我们要建小堆）

我们可以看到打印结果为一个堆

如果说我们有一个数组，不是堆，但是想将其调整成堆，那么看代码：

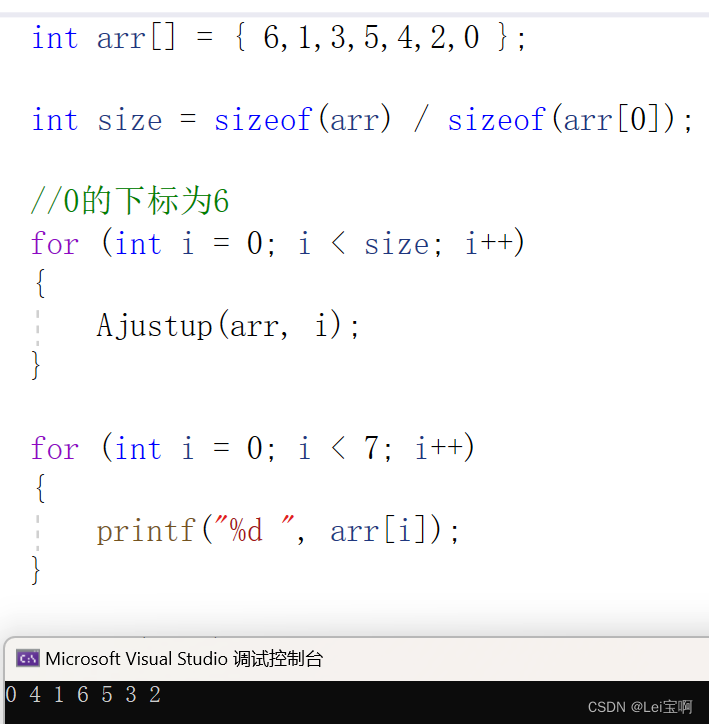
结果为一个堆~

---

堆向下调整建堆：

思路及代码：

不论我们有没有堆，调整方式都可以按照如下方法去调整建堆，代码如下：