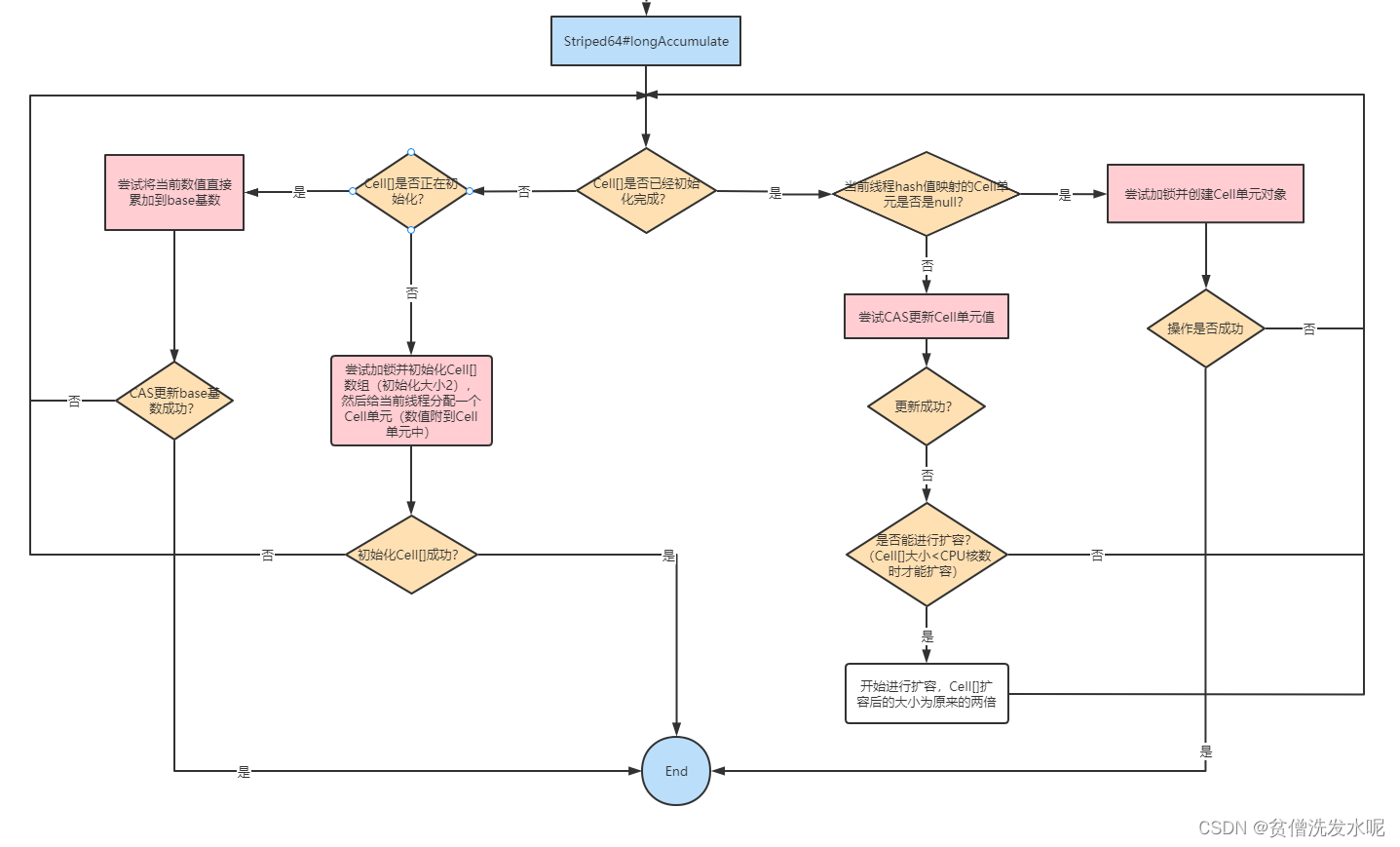
一、数组理论基础
数组是存放在连续内存空间上的相同类型数据的集合。
数组可以方便的通过下标索引的方式获取到下标下对应的数据。
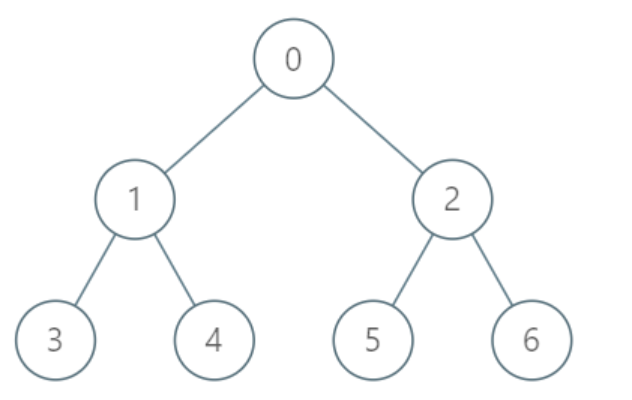
举一个字符数组的例子如图:
需要两点注意的是
- 数组下标都是从0开始的。
- 数组内存空间的地址是连续的
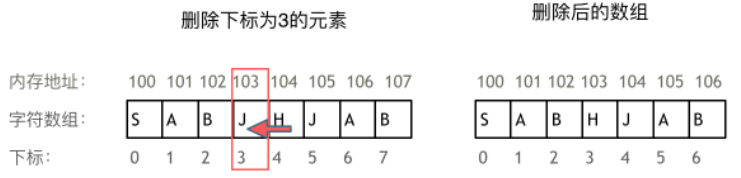
正是因为数组的在内存空间的地址是连续的,所以我们在删除或者增添元素的时候,就难免要移动其他元素的地址。
例如删除下标为3的元素,需要对下标为3的元素后面的所有元素都要做移动操作,如图所示:
二、704. 二分查找力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台备战技术面试?力扣提供海量技术面试资源,帮助你高效提升编程技能,轻松拿下世界 IT 名企 Dream Offer。 https://leetcode.cn/problems/binary-search/
https://leetcode.cn/problems/binary-search/
例题:
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
示例 1:
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4 示例 2:
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1 提示:
- 你可以假设 nums 中的所有元素是不重复的。
- n 将在 [1, 10000] 之间。
- nums 的每个元素都将在 [-9999, 9999] 之间。
算法公开课:手把手带你撕出正确的二分法 | 二分查找法 | 二分搜索法 | LeetCode:704. 二分查找_哔哩哔哩_bilibili
第一种写法:定义在左闭右闭的区间里[left, right] ,(这个非常重要)
区间定义二分法的代码如何写:首先定义target在[left, right]区间!
因此有这两点:①while (left <= right) 要使用 <=,因为:left == right是有意义的,所以:使用 <=
②if (nums[middle] > target) right 要赋值为 middle - 1,因为:当前这个nums[middle]一定不是target,那么接下来要查找的左区间结束下标位置就是 middle - 1
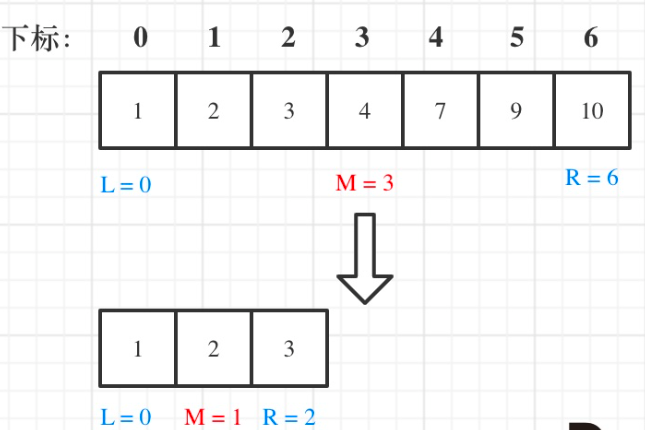
例如:在数组[1,2,3,4,7,9,10]中查找元素2,如图所示:

public class day01 {
public static void main(String[] args) {
int nums[] = {1, 3, 7, 9};
int target = 7;
System.out.println(search(nums, target));
}
//1.左闭右闭的情况
public static int search(int nums[], int target) {
//避免当target 小于nums[0] ,nums[nums.lenth-1]时多循环运算
if (target < nums[0] || target > nums[nums.length - 1]) {
return -1;// 这里呢进行一个排除 如果说目标的值小于最小,大于最大,那就直接退出
}
int left = 0;
int right = nums.length - 1;// 定义target在左闭右闭的区间里,[left, right]
while (left <= right) { // 当left==right,区间[left, right]依然有效,所以用 <=
int middle = left + ((right - left) / 2);// 防止溢出 等同于(left + right)/2
if (nums[middle] == target)
return middle;// 数组中找到目标值,直接返回下标
else if (nums[middle] < target)
left = middle + 1;// target 在右区间,所以[middle + 1, right]
else if (nums[middle] > target)
right = middle - 1; // target 在左区间,所以[left, middle - 1]
}
return -1;
}
}第二种写法:左闭右开的区间里[left, right) 那么二分法的边界处理方式则截然不同。
有如这两点:
- while (left < right),这里使用 < ,因为left == right在区间[left, right)是没有意义的
- if (nums[middle] > target) right 更新为 middle,因为:当前nums[middle]不等于target,去左区间继续寻找,而寻找区间是左闭右开区间, 所以:right更新为middle,即:下一个查询区间不会去比较nums[middle]
在数组:1,2,3,4,7,9,10中查找元素2,如图所示:(注意和方法一的区别)


//2.左闭右开的情况
public static int search2(int nums[], int target) {
//避免当target 小于nums[0] ,nums[nums.lenth-1]时多循环运算
if (target < nums[0] || target > nums[nums.length - 1]) {
return -1;// 这里呢进行一个排除 如果说目标的值小于最小,大于最大,那就直接退出
}
int left = 0;
int right = nums.length - 1;// 定义target在左闭右开的区间里,即:[left, right)
while (left < right) { // 因为left == right的时候,在[left, right)是无效的空间,所以使用 <
int middle = left + ((right - left) >> 1);
if (nums[middle] > target)
return middle; // target 在左区间,在[left, middle)中
else if (nums[middle] < target)
left = middle + 1;// target 在右区间,在[middle + 1, right)中
else if (nums[middle] == target)
return middle; // 数组中找到目标值,直接返回下标
}
return -1;
}三、总结
总体代码:
package com.chapter.one.shuzu;
public class day01 {
public static void main(String[] args) {
int nums[] = {1, 3, 7, 9};
int target = 7;
System.out.println(search2(nums, target));
}
//1.左闭右闭的情况
public static int search(int nums[], int target) {
//避免当target 小于nums[0] ,nums[nums.lenth-1]时多循环运算
if (target < nums[0] || target > nums[nums.length - 1]) {
return -1;// 这里呢进行一个排除 如果说目标的值小于最小,大于最大,那就直接退出
}
int left = 0;
int right = nums.length - 1;// 定义target在左闭右闭的区间里,[left, right]
while (left <= right) { // 当left==right,区间[left, right]依然有效,所以用 <=
int middle = left + ((right - left) / 2);// 防止溢出 等同于(left + right)/2
if (nums[middle] == target)
return middle;// 数组中找到目标值,直接返回下标
else if (nums[middle] < target)
left = middle + 1;// target 在右区间,所以[middle + 1, right]
else if (nums[middle] > target)
right = middle - 1; // target 在左区间,所以[left, middle - 1]
}
return -1;
}
//2.左闭右开的情况
public static int search2(int nums[], int target) {
//避免当target 小于nums[0] ,nums[nums.lenth-1]时多循环运算
if (target < nums[0] || target > nums[nums.length - 1]) {
return -1;// 这里呢进行一个排除 如果说目标的值小于最小,大于最大,那就直接退出
}
int left = 0;
int right = nums.length - 1;// 定义target在左闭右开的区间里,即:[left, right)
while (left < right) { // 因为left == right的时候,在[left, right)是无效的空间,所以使用 <
int middle = left + ((right - left) >> 1);
if (nums[middle] > target)
return middle; // target 在左区间,在[left, middle)中
else if (nums[middle] < target)
left = middle + 1;// target 在右区间,在[middle + 1, right)中
else if (nums[middle] == target)
return middle; // 数组中找到目标值,直接返回下标
}
return -1;
}
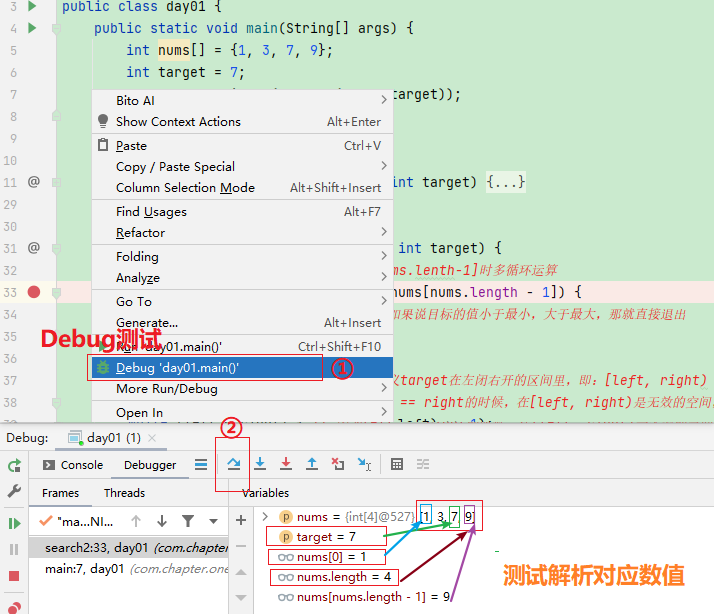
}Debug测试解析:
 ①对区间的定义要理解清楚;
①对区间的定义要理解清楚;
②在循环中没有始终坚持根据查找区间的定义来做边界处理;
③区间的定义就是不变量,那么在循环中坚持根据查找区间的定义来做边界处理,就是循环不变量规则;
总结本篇:两种常见的区间定义,给出了两种二分法的写法,每一个边界为什么这么处理,都根据区间的定义做了详细介绍。
------------------希望可以帮助到更多学习Java的小伙伴,不懂或者有疑惑的可以随时来问我哦!
-------------@程序员~小鱼儿