一、直接插入排序

1、插入排序思想

直接插入排序就是将待排序的记录按照它的关键码值插入到一个已经排好序的有序序列中，直到所有的记录都插入完，得到一个新的有序序列。

插入排序的思想就像我们平时玩扑克牌理牌时一样，将每张牌逐个插入到一个有序的牌的序列里，最终所有的牌都是有序的。

2、程序代码

//插入排序
void InsertSort(int* a, int n)
{
	for (int i = 0; i < n-1; i++)
	{
		//end可看作从左至右有序的最后一个数的下标
		int end = i;
		int tmp = a[end + 1];
		
		while (end >= 0)
		{
			if (tmp < a[end])
			{
				a[end + 1] = a[end];
			}
			else
			{
				break;
			}
			end--;
		}
		//此时tmp的值大于或等于下标为end的值，所以插入在它的后面
		a[end+1] = tmp;
	}
}

代码分析：

当插入第i(i>=1)个元素时，前面的a[0],a[1],…,a[i-1]已经排好序，此时用a[i]的排序码与a[i-1],a[i-2],…的排序码顺序进行比较，找到插入位置即将a[i]插入，原来位置上的元素顺序后移

直接插入排序是一种稳定的排序算法，元素集合越接近有序，直接插入排序算法的时间效率越高，它的时间复杂度为O(n²)，空间复杂度为O(1)

3、测试

//打印数组
void PrintArray(int* a, int n)
{
	for (int i = 0; i < n; i++)
	{
		printf("%d ", a[i]);
	}
	printf("\n");
}
//测试直接插入排序
void TestInsertSort()
{
    //任意建立一组无序的数
	int a[] = { 9,1,2,5,7,4,8,6,3,5,1,2,3,5,1,8,3 };
	InsertSort(a, sizeof(a) / sizeof(int));
	PrintArray(a, sizeof(a) / sizeof(int));
}

int main()
{
	printf("直接插入排序：\n");
	TestInsertSort();
	return 0;
}

二、希尔排序

1、什么是希尔排序

希尔排序法又称缩小增量法。希尔排序的基本思想是：先选定一个整数gap，把待排序数列中所有记录分成个gap个组，所有距离为gap的记录分在同一组内，并对每一组内的记录进行排序。然后缩小gap，可以取它的一半，重复上述分组和排序的工作。当gap到达1时，该数列便已有序。

当gap=1时相当于直接插入排序。所以希尔排序可以拆分为预排序和直接插入排序两部分：

1. 预排序：当gap大于1时，预排序可以让大的数更快地到序列后面，小的更快到前面，gap越大跳的越快越不接近有序，gap越小跳的越慢，越接近有序
2. 直接插入排序：gap不断减小，当gap为1时相当于直接插入排序，进行最后一次直接插入排序后数列便已有序

2、希尔排序图解

对如下图数列用希尔排序算法进行排序：

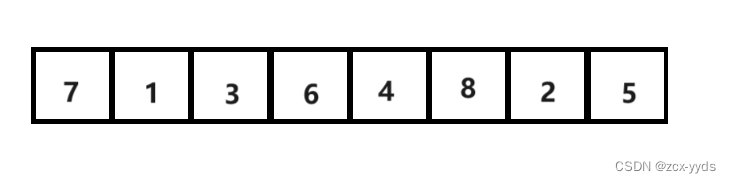
该数列一共有8个数，我们选定最初的gap值为8/2=4，相隔4的数为一组，如下图，同一组数颜色相同

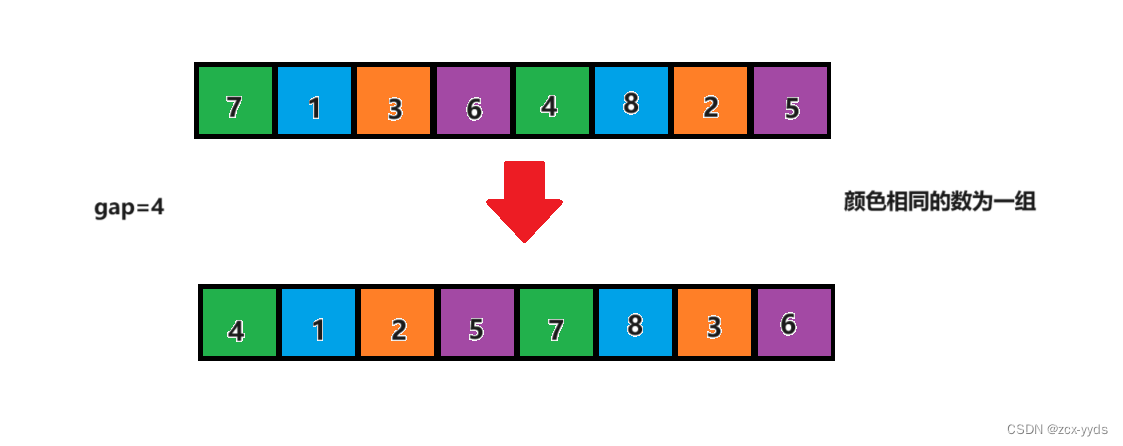
对每一组排序了之后，gap再除2变为2

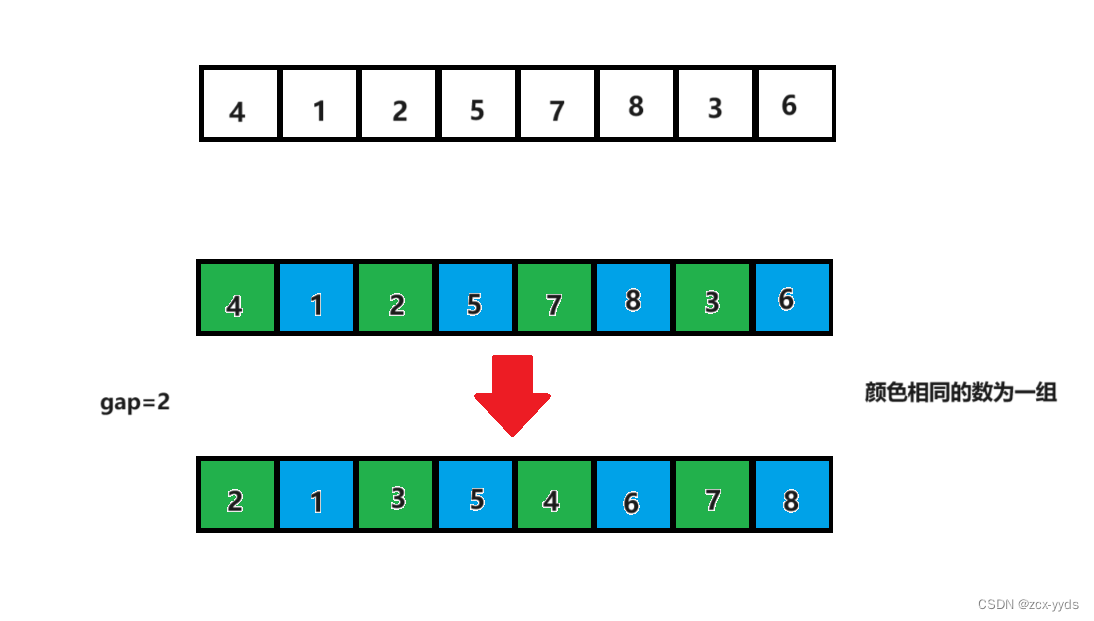
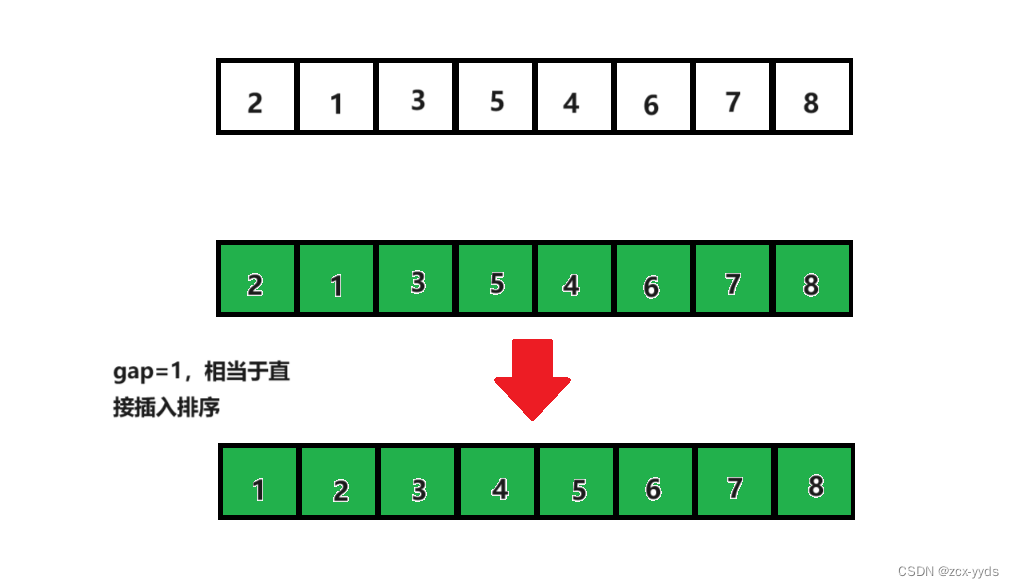
对每一组排序了之后，gap再除2变为1，此时相当于直接插入排序

3、程序代码

//希尔排序
void ShellSort(int* a, int n)
{
	//gap进入循环后会先除2
	int gap = n ;

	while (gap > 1)
	{
		gap /= 2;
		for (int i = 0; i < n - gap; i++)
		{
			int end = i;
			int tmp = a[end + gap];
			while (end >= 0)
			{
				if (tmp < a[end])
				{
					a[end + gap] = a[end];
				}
				else
				{
					break;
				}
				end -= gap;
			}
			a[end + gap] = tmp;
		}
	}	
}

希尔排序是不稳定的，它是对直接插入排序的优化，因为gap的取值方法不止一种，导致希尔排序的时间复杂度很难去计算

4、测试

//打印数组
void PrintArray(int* a, int n)
{
	for (int i = 0; i < n; i++)
	{
		printf("%d ", a[i]);
	}
	printf("\n");
}
//测试希尔排序
void TestShellSort()
{
    //任意建立一组无序的数
    int a[] = { 9,1,2,5,7,4,8,6,3,5,1,2,3,5,1,8,3 };
	ShellSort(a, sizeof(a) / sizeof(int));
	PrintArray(a, sizeof(a) / sizeof(int));
}

int main()
{
	printf("希尔排序：\n");
	TestShellSort();
	return 0;
}