文章目录
- 整体
- 记忆宫殿
- 角度/分类/串联线——从小到大
- 角度/分类/串联线2——求长度,面积,角度
- 局部
- 数字编码
- 口诀法
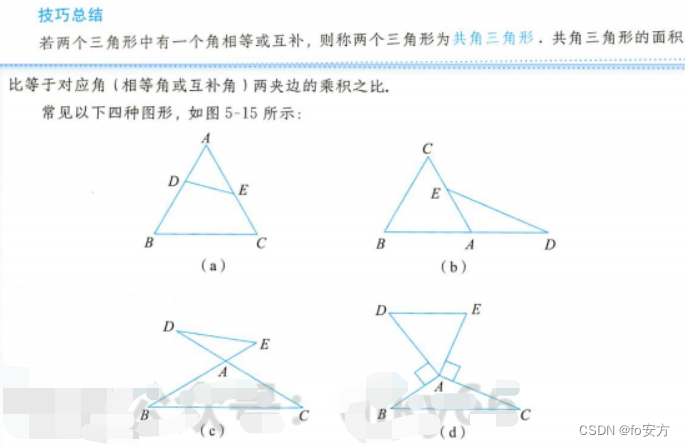
- 五大模型/共角定理、风筝模型、蝴蝶模型
- 转化图像法
- 特点法
- 公式推导法:公式推导掌握数学公式
- 射影定理
- 共角定理
- 燕尾定理
- 蝴蝶定理/模型
- 三角形的四心,内切圆半径,外接圆半径
- 汇总法
- 面积公式汇总
- 定理模型汇总/图形结合法
- 鸟头定理/共角模型记忆汇总
整体
整体要点依赖宫殿记忆
记忆宫殿
学习记忆——宫殿篇——记忆宫殿——记忆桩——单间+客厅+厨房+厕所+书房+院子空间够大,可以将“代数”和“几何”放进去,代数即几何,特别适合放一个空间。
不同的角度或者串联逻辑线,方便加到印象深刻的记忆桩中。知识点串联起来的线,可以使得有逻辑的放置物品,更容易的想起来顺序来。
角度/分类/串联线——从小到大
从三角形的周边的角,边,到中间的“心”,整体的“形状”,“面积”
- 角:三角关系,内角和定理。
- 边:三边关系,中线定理,角平分线。
(1)勾股定理:常见勾股数(3,4,5),(6,8,10),(5,12,13),(7,24,25),(8,15,17),(9,12,15)
(2)中线定理:AD为BC边上的中线, A B 2 + A C 2 = 2 ( A D 2 + B D 2 ) AB^2+AC^2=2(AD^2+BD^2) AB2+AC2=2(AD2+BD2)
塞瓦定理: - 边与角:边角关系,正弦定理,余弦定理。
(1)正弦定理: a s i n A = b s i n B = c s i n C = 2 R 外 \frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}=2R_外 sinAa=sinBb=sinCc=2R外, R 外 = a b c 4 S R_外=\frac{abc}{4S} R外=4Sabc
(2)余弦定理: { a 2 = b 2 + c 2 − 2 b c c o s A , b 2 = a 2 + c 2 − 2 a c c o s B , c 2 = a 2 + b 2 − 2 a b c o s C \begin{cases} a^2=b^2+c^2-2bccosA, \\ b^2=a^2+c^2-2accosB, \\ c^2=a^2+b^2-2abcosC \end{cases} ⎩ ⎨ ⎧a2=b2+c2−2bccosA,b2=a2+c2−2accosB,c2=a2+b2−2abcosC
{ c o s A = b 2 + c 2 − a 2 2 b c , c o s B = a 2 + c 2 − b 2 2 a c , c o s C = a 2 + b 2 − c 2 2 a b \begin{cases} cosA=\frac{b^2+c^2-a^2}{2bc}, \\ cosB=\frac{a^2+c^2-b^2}{2ac}, \\ cosC=\frac{a^2+b^2-c^2}{2ab} \end{cases} ⎩ ⎨ ⎧cosA=2bcb2+c2−a2,cosB=2aca2+c2−b2,cosC=2aba2+b2−c2
(3)张角定理:
(4)边比值:
等腰直角三角形的三边之比: 1 : 1 : 2 1:1:\sqrt{2} 1:1:2
内角为 3 0 o 30^o 30o、 6 0 o 60^o 60o、 9 0 o 90^o 90o的直角三角形三边之比为: 1 : 3 : 2 1:\sqrt{3}:2 1:3:2
等边三角形高与边的比为: 3 : 2 \sqrt{3}:2 3:2 - 心:四线五心(内心,外心,垂心,重心,中心)
(1)内心:角平分线的交点,是内切圆的圆心,到三边的距离相等。 一般三角形, S = r 2 ( a + b + c ) , S 为面积, r 为内切圆半径, a , b , c 是三边 一般三角形,S=\frac{r}{2}(a+b+c),S为面积,r为内切圆半径,a,b,c是三边 一般三角形,S=2r(a+b+c),S为面积,r为内切圆半径,a,b,c是三边; 一般三角形,内切圆半径 r = 2 S a + b + c 一般三角形,内切圆半径r=\frac{2S}{a+b+c} 一般三角形,内切圆半径r=a+b+c2S; 直角三角形,内切圆半径 r = a + b − c 2 直角三角形,内切圆半径r=\frac{a+b-c}{2} 直角三角形,内切圆半径r=2a+b−c; 直角三角形,内切圆半径 r = 3 a 6 直角三角形,内切圆半径r=\frac{\sqrt{3}a}{6} 直角三角形,内切圆半径r=63a。
(2)外心:三边的中垂线的交点,是外接圆的圆心,到三个顶点的距离相等。 S = a b c 4 R , S 为面积, R 为外接圆半径 S=\frac{abc}{4R},S为面积,R为外接圆半径 S=4Rabc,S为面积,R为外接圆半径。
(3)重心:三条中线的交点。重心将三角形分为三个面积相等的三角形,衷心将中线分成 2 : 1 2:1 2:1两段。已知三角形三个顶点的坐标( x 1 x_1 x1, y 1 y_1 y1)、( x 2 x_2 x2, y 2 y_2 y2)、( x 3 x_3 x3, y 3 y_3 y3),则重心坐标为( x 1 + x 2 + x 3 3 \frac{x_1+x_2+x_3}{3} 3x1+x2+x3, y 1 + y 2 + y 3 3 \frac{y_1+y_2+y_3}{3} 3y1+y2+y3)
(4)垂心:三条高的交点。锐角三角形的垂心在三角形内;直角三角形的垂心在直角顶点上;钝角三角形的垂心在三角形外。 - 面积:通用公式,特殊公式。/ 多少,最值。/ 定理:求长度定理,求面积定理。/ 五个面积公式。/利用底高,夹角,三边计算面积
(1)求面积:求面积汇总公式: S = 1 2 a h [ 底高 → 燕尾定理 ] = 1 2 a b s i n C [ 夹角 → 共角定理 ] = p ( p − a ) ( p − b ) ( p − c ) [ 三边 ] = r p [ 内心 ] = a b c 4 R [ 外心 ] S=\frac{1}{2}ah[底高→燕尾定理]=\frac{1}{2}absinC[夹角→共角定理]=\sqrt{p(p-a)(p-b)(p-c)}[三边]=rp[内心]=\frac{abc}{4R}[外心] S=21ah[底高→燕尾定理]=21absinC[夹角→共角定理]=p(p−a)(p−b)(p−c)[三边]=rp[内心]=4Rabc[外心],其中,h是a边上的高,∠C是a,b边所夹的角, p = 1 2 ( a + b + c ) p=\frac{1}{2}(a+b+c) p=21(a+b+c),r为三角形内切圆的半径,R为三角形外接圆的半径。
(2)面积比:五大模型:等面积模型,鸟头模型/共角模型,相似模型,燕尾模型,风筝模型,蝴蝶模型。
根据公式推导的原理,可以得出:
三角形底高面积公式→燕尾定理
三角形sin夹角面积公式→鸟头定理/共角模型
相似定理→射影定理,蝴蝶定理 - 面积与边:五大模型:等面积模型,鸟头模型/共角模型,相似模型,燕尾模型,风筝模型,蝴蝶模型。(有动物的定理都跟“面积比与线段比”有关)
(1)鸟头定理:两个三角形中有一个角相等或互补,两个三角形称为共角三角形,共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。(触发条件:出现共角或等角的三角形)【分为三大模型:共角模型,对顶角模型,补角模型。】
(2)燕尾定理:共顶点的两个形如燕尾的三角形面积比等于底边比。(触发条件:三角形内部有一个点与三顶点连线求面积)
(3)风筝定理:
(4)蝴蝶定理: - 形状:相似,全等。
等腰直角三角形:三边之比满足 1 : 1 : 2 1:1:\sqrt{2} 1:1:2。
等边三角形:三个内角相等或者四心合一。
(1)相似
① 相似三角形(相似图形)对应边的比相等(即为相似比)。
② 相似三角形(相似图形)的高、中线、角平分线的比也等于相似比。
③ 相似三角形(相似图形)的周长比等于相似比。
④ 相似三角形(相似图形)的面积比等于相似比的平方。
根据上述提到的“心”,想到是否可以用“身体”这个记忆桩进行记忆https://blog.csdn.net/stqer/article/details/132844351

头发
眼睛
鼻子
嘴巴
脖子
肩膀
前胸→心:五心
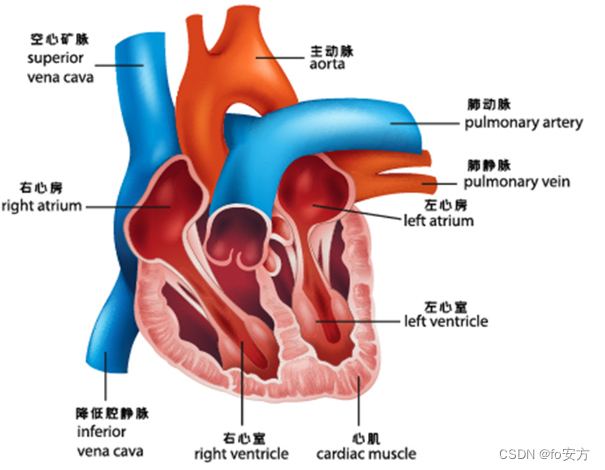
肚子
大腿
脚
角度/分类/串联线2——求长度,面积,角度
- 求长度
直角三角形求长度,优先勾股定理;
直角三角形中做高求长度,优先射影定理; - 求面积
(1)单个三角形:三大面积公式: S = 1 2 a h [ 利用底高 ] = 1 2 a b s i n C ( C 是 a , b 边所夹的角 ) [ 利用夹角 ] = p ( p − a ) ( p − b ) ( p − c ) ( p = 1 2 ( a + b + c ) ) [ 利用三边 ] S=\frac{1}{2}ah[利用底高]=\frac{1}{2}absinC(C是a,b边所夹的角)[利用夹角]=\sqrt{p(p-a)(p-b)(p-c)}(p=\frac{1}{2}(a+b+c))[利用三边] S=21ah[利用底高]=21absinC(C是a,b边所夹的角)[利用夹角]=p(p−a)(p−b)(p−c)(p=21(a+b+c))[利用三边]
S = 1 2 a h = 1 2 a b s i n C = p ( p − a ) ( p − b ) ( p − c ) = r p = a b c 4 R S=\frac{1}{2}ah=\frac{1}{2}absinC=\sqrt{p(p-a)(p-b)(p-c)}=rp=\frac{abc}{4R} S=21ah=21absinC=p(p−a)(p−b)(p−c)=rp=4Rabc,其中,h是a边上的高,∠C是a,b边所夹的角, p = 1 2 ( a + b + c ) p=\frac{1}{2}(a+b+c) p=21(a+b+c),r为三角形内切圆的半径,R为三角形外接圆的半径。
(2)两个三角形:
① 出现共角或等角的三角形,用鸟头模型。
② 三角形内部有一个点与三顶点连线求面积,用燕尾模型。 - 求角度
- 三角形的四心五线
局部
局部各个知识点,利用多种技巧进行记忆
数字编码
常见勾股数(1,1, 2 \sqrt{2} 2),(1, 3 \sqrt{3} 3,2),(3,4,5),(6,8,10),(5,12,13),(7,24,25),(8,15,17),(9,12,15):
3是弓,4是旗,5是钩/手掌,6是勺子,7是镰刀,8是葫芦,9球拍,10是衣领,12是婴儿,13是医生,15是鹦鹉,17是仪器,24盒子,25是二胡。
1,1,
2
\sqrt{2}
2:点两只蜡烛,找一只更好鸭。
1,
3
\sqrt{3}
3,2:
3,4,5:用手掌,拉弓和举旗。
6,8,10:
5,12,13:钩子勾住婴儿的是医生。用手掌勾住婴儿的是医生。
7,24,25:用镰刀打开盒子,里面放着二胡。
8,15,17:
9,12,15:球拍,婴儿,鹦鹉。婴儿用球拍打鹦鹉。
或者

3,4,5:SHW=是华为
6,8,10:GBYD=改变移动
面积公式: S = 1 2 a h [ 利用底高 ] = 1 2 a b s i n C ( C 是 a , b 边所夹的角 ) [ 利用夹角 ] = p ( p − a ) ( p − b ) ( p − c ) ( p = 1 2 ( a + b + c ) ) [ 利用三边 ] S=\frac{1}{2}ah[利用底高]=\frac{1}{2}absinC(C是a,b边所夹的角)[利用夹角]=\sqrt{p(p-a)(p-b)(p-c)}(p=\frac{1}{2}(a+b+c))[利用三边] S=21ah[利用底高]=21absinC(C是a,b边所夹的角)[利用夹角]=p(p−a)(p−b)(p−c)(p=21(a+b+c))[利用三边]
内角为
4
5
o
45^o
45o、
4
5
o
45^o
45o、
9
0
o
90^o
90o/等腰直角三角形的三边之比:
1
:
1
:
2
1:1:\sqrt{2}
1:1:2
内角为
3
0
o
30^o
30o、
6
0
o
60^o
60o、
9
0
o
90^o
90o的直角三角形三边之比为:
1
:
3
:
2
1:\sqrt{3}:2
1:3:2
内角为
6
0
o
60^o
60o、
6
0
o
60^o
60o、
6
0
o
60^o
60o等边三角形高与边的比为:
3
:
2
\sqrt{3}:2
3:2
30森林,45师傅,60榴莲,90酒瓶/精灵,直角z闪电,1蜡烛,根号3根号伞,2鸭子
两个师傅拿着酒瓶进行三边比,(两个人需要)两根蜡烛跟(一只)好鸭。
森林里面有个爱吃榴莲的精灵进行三边比,(一个精灵只需)一个蜡烛,跟(一把)好伞,鸭子。
三颗榴莲高边比,跟一把好伞,鸭子。
内心:角平分线的交点,是内切圆的圆心,到三边的距离相等。 一般三角形, S = r 2 ( a + b + c ) , S 为面积, r 为内切圆半径, a , b , c 是三边 一般三角形,S=\frac{r}{2}(a+b+c),S为面积,r为内切圆半径,a,b,c是三边 一般三角形,S=2r(a+b+c),S为面积,r为内切圆半径,a,b,c是三边; 一般三角形,内切圆半径 r = 2 S a + b + c 一般三角形,内切圆半径r=\frac{2S}{a+b+c} 一般三角形,内切圆半径r=a+b+c2S; 直角三角形,内切圆半径 r = a + b − c 2 直角三角形,内切圆半径r=\frac{a+b-c}{2} 直角三角形,内切圆半径r=2a+b−c; 直角三角形,内切圆半径 r = 3 a 6 直角三角形,内切圆半径r=\frac{\sqrt{3}a}{6} 直角三角形,内切圆半径r=63a。
口诀法
五大模型/共角定理、风筝模型、蝴蝶模型
三角形重心:重心连线二比一,面积分成六个一
共角模型:同角补角面积比,结果都是腰积比
射影定理:
影子长乘斜边长,等于直角边平方
斜边两半相互乘,等于斜边高平方
风筝模型:对角相乘面积等
蝴蝶模型:
梯形对角连一连,分成四个小三角
从小到大面积比,底的平方夹乘积
转化图像法
学习记忆——数学篇——转图像记忆法
S = 1 2 a h = 1 2 a b s i n C = p ( p − a ) ( p − b ) ( p − c ) = r p = a b c 4 R S=\frac{1}{2}ah=\frac{1}{2}absinC=\sqrt{p(p-a)(p-b)(p-c)}=rp=\frac{abc}{4R} S=21ah=21absinC=p(p−a)(p−b)(p−c)=rp=4Rabc,其中,h是a边上的高,∠C是a,b边所夹的角, p = 1 2 ( a + b + c ) p=\frac{1}{2}(a+b+c) p=21(a+b+c),r为三角形内切圆的半径,R为三角形外接圆的半径。
转换:“
p
=
1
2
(
a
+
b
+
c
)
p=\frac{1}{2}(a+b+c)
p=21(a+b+c)”-三边的一半,半周长,拌粥;r-内切圆半径,内切半斤;abc-边长乘积-边长成绩;R-外接半斤。
面积等于内切半斤(肉)拌粥;也等于=变成鸡初一时外接半斤(肉)。
引用:
S
=
1
2
a
h
[
底高
]
=
1
2
a
b
s
i
n
C
[
夹角
]
=
p
(
p
−
a
)
(
p
−
b
)
(
p
−
c
)
[
三边
]
=
r
p
[
内心
]
=
a
b
c
4
R
[
外心
]
S=\frac{1}{2}ah[底高]=\frac{1}{2}absinC[夹角]=\sqrt{p(p-a)(p-b)(p-c)}[三边]=rp[内心]=\frac{abc}{4R}[外心]
S=21ah[底高]=21absinC[夹角]=p(p−a)(p−b)(p−c)[三边]=rp[内心]=4Rabc[外心],其中,h是a边上的高,∠C是a,b边所夹的角,
p
=
1
2
(
a
+
b
+
c
)
p=\frac{1}{2}(a+b+c)
p=21(a+b+c),r为三角形内切圆的半径,R为三角形外接圆的半径。
内心:角平分线的交点,是内切圆的圆心,到三边的距离相等。
一般三角形,
S
=
r
2
(
a
+
b
+
c
)
,
S
为面积,
r
为内切圆半径,
a
,
b
,
c
是三边
一般三角形,S=\frac{r}{2}(a+b+c),S为面积,r为内切圆半径,a,b,c是三边
一般三角形,S=2r(a+b+c),S为面积,r为内切圆半径,a,b,c是三边;
外心:三边的中垂线的交点,是外接圆的圆心,到三个顶点的距离相等。
S
=
a
b
c
4
R
,
S
为面积,
R
为外接圆半径
S=\frac{abc}{4R},S为面积,R为外接圆半径
S=4Rabc,S为面积,R为外接圆半径。
特点法
常用角度的正弦、余弦、正切值:
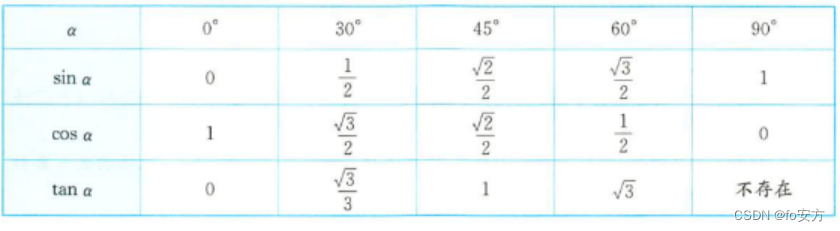

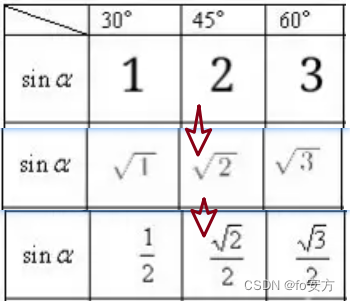
2分之:根号1、根号2、根号3
公式推导法:公式推导掌握数学公式
根据公式推导的原理,可以找出:
三角形底高面积公式→燕尾定理
三角形sin夹角面积公式→鸟头定理/共角模型
相似定理→射影定理,蝴蝶定理
射影定理
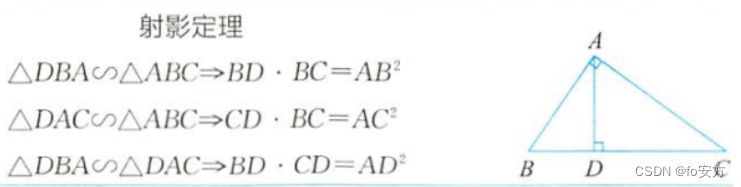
共角定理

S
=
1
2
a
h
[
底高
]
=
1
2
a
b
s
i
n
C
[
夹角
]
=
p
(
p
−
a
)
(
p
−
b
)
(
p
−
c
)
[
三边
]
=
r
p
[
内心
]
=
a
b
c
4
R
[
外心
]
S=\frac{1}{2}ah[底高]=\frac{1}{2}absinC[夹角]=\sqrt{p(p-a)(p-b)(p-c)}[三边]=rp[内心]=\frac{abc}{4R}[外心]
S=21ah[底高]=21absinC[夹角]=p(p−a)(p−b)(p−c)[三边]=rp[内心]=4Rabc[外心],其中,h是a边上的高,∠C是a,b边所夹的角,
p
=
1
2
(
a
+
b
+
c
)
p=\frac{1}{2}(a+b+c)
p=21(a+b+c),r为三角形内切圆的半径,R为三角形外接圆的半径。中的夹角面积公式可推出“共角定理”,“共角”与“夹角”有关,进而跟
S
=
1
2
a
b
s
i
n
C
[
夹角
]
S=\frac{1}{2}absinC[夹角]
S=21absinC[夹角]有关。
可以将“共角定理”也放到“面积汇总公式”中去,如下:
S = 1 2 a h [ 底高 ] = 1 2 a b s i n C [ 夹角 → 共角定理 ] = p ( p − a ) ( p − b ) ( p − c ) [ 三边 ] = r p [ 内心 ] = a b c 4 R [ 外心 ] S=\frac{1}{2}ah[底高]=\frac{1}{2}absinC[夹角→共角定理]=\sqrt{p(p-a)(p-b)(p-c)}[三边]=rp[内心]=\frac{abc}{4R}[外心] S=21ah[底高]=21absinC[夹角→共角定理]=p(p−a)(p−b)(p−c)[三边]=rp[内心]=4Rabc[外心],其中,h是a边上的高,∠C是a,b边所夹的角, p = 1 2 ( a + b + c ) p=\frac{1}{2}(a+b+c) p=21(a+b+c),r为三角形内切圆的半径,R为三角形外接圆的半径。
燕尾定理

与面积公式的:
S
=
1
2
a
h
[
底高
]
S=\frac{1}{2}ah[底高]
S=21ah[底高]有关系,可以将“燕尾定理”关联到面积公式中,可得:
S
=
1
2
a
h
[
底高
→
燕尾定理
]
S=\frac{1}{2}ah[底高→燕尾定理]
S=21ah[底高→燕尾定理],通过“底高”可以推出燕尾定理。
蝴蝶定理/模型
任意梯形被对角线分成面积为
S
1
S_1
S1,
S
2
S_2
S2,
S
3
S_3
S3,
S
4
S_4
S4的四部分,则有
S
1
:
S
2
:
S
4
:
S
3
=
a
2
:
a
b
:
a
b
:
b
2
S_1:S_2:S_4:S_3=a^2:ab:ab:b^2
S1:S2:S4:S3=a2:ab:ab:b2。
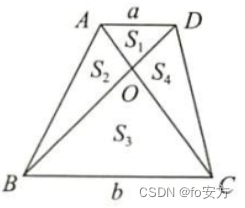
由相似定理可推出:蝴蝶定理
三角形的四心,内切圆半径,外接圆半径

汇总法
将同属性的事物放一起记忆,比如汇总同一个知识点的不同记忆技巧,放一起看,选一个你最喜欢的/最让你印象深刻的。
面积公式汇总
面积公式汇总: S = 1 2 a h [ 底高 ] = 1 2 a b s i n C [ 夹角 ] = p ( p − a ) ( p − b ) ( p − c ) [ 三边 ] = r p [ 内心 ] = a b c 4 R [ 外心 ] S=\frac{1}{2}ah[底高]=\frac{1}{2}absinC[夹角]=\sqrt{p(p-a)(p-b)(p-c)}[三边]=rp[内心]=\frac{abc}{4R}[外心] S=21ah[底高]=21absinC[夹角]=p(p−a)(p−b)(p−c)[三边]=rp[内心]=4Rabc[外心],其中,h是a边上的高,∠C是a,b边所夹的角, p = 1 2 ( a + b + c ) p=\frac{1}{2}(a+b+c) p=21(a+b+c),r为三角形内切圆的半径,R为三角形外接圆的半径。
定理模型汇总/图形结合法
平面几何五大模型
- 等面积模型:两个三角形高之比为 h 1 : h 2 h_1:h_2 h1:h2,底之比为 a 1 : a 2 a_1:a_2 a1:a2,面积之比为 S 1 : S 2 = a 1 h 1 : a 2 h 2 S_1:S_2=a_1h_1:a_2h_2 S1:S2=a1h1:a2h2
- 共角模型:
S
△
A
B
C
:
S
△
A
D
E
=
(
A
B
⋅
A
C
)
:
(
A
D
⋅
A
E
)
S_{△ABC}:S_{△ADE}=(AB·AC):(AD·AE)
S△ABC:S△ADE=(AB⋅AC):(AD⋅AE)
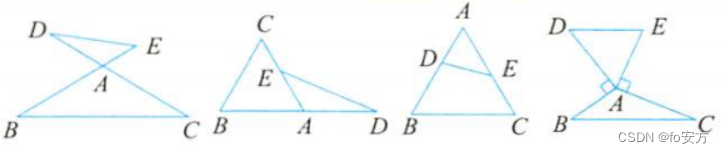
- 相似模型:
- 燕尾模型:
S △ A O B : S △ A O C = B D : D C S_{△AOB}:S_{△AOC}=BD:DC S△AOB:S△AOC=BD:DC
S △ A O B : S △ C O B = A E : C E S_{△AOB}:S_{△COB}=AE:CE S△AOB:S△COB=AE:CE
S △ B O C : S △ A O C = B F : A F S_{△BOC}:S_{△AOC}=BF:AF S△BOC:S△AOC=BF:AF
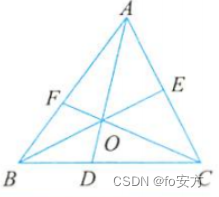
- 风筝模型:
S
1
:
S
4
=
S
2
:
S
3
S_1:S_4=S_2:S_3
S1:S4=S2:S3,
S
1
:
S
4
=
S
2
:
S
3
S_1:S_4=S_2:S_3
S1:S4=S2:S3
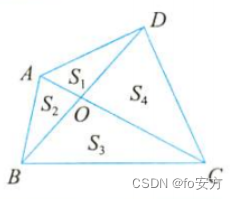
- 蝴蝶模型:任意梯形被对角线分成面积为 S 1 S_1 S1, S 2 S_2 S2, S 3 S_3 S3, S 4 S_4 S4的四部分,则有 S 1 : S 2 : S 4 : S 3 = a 2 : a b : a b : b 2 S_1:S_2:S_4:S_3=a^2:ab:ab:b^2 S1:S2:S4:S3=a2:ab:ab:b2。
鸟头定理/共角模型记忆汇总
-
图形结合法: S △ A B C : S △ A D E = ( A B ⋅ A C ) : ( A D ⋅ A E ) S_{△ABC}:S_{△ADE}=(AB·AC):(AD·AE) S△ABC:S△ADE=(AB⋅AC):(AD⋅AE)

-
公式推导法:
夹角面积公式 S = 1 2 a b s i n C [ 夹角 ] S=\frac{1}{2}absinC[夹角] S=21absinC[夹角]可推出“共角定理”,“共角”与“夹角”有关,可以将“共角定理”也放到“面积汇总公式”中去,如下:
S = 1 2 a h [ 底高 ] = 1 2 a b s i n C [ 夹角 → 共角定理 ] S=\frac{1}{2}ah[底高]=\frac{1}{2}absinC[夹角→共角定理] S=21ah[底高]=21absinC[夹角→共角定理] -
口诀法:
共角模型:同角补角面积比,结果都是腰积比
入栏需看——学习记忆