文章目录
- 前言
- 一、常见的排序算法
- 二、归并排序的基本思想
- 三、归并排序
- 3.1 归并排序的递归版本
- 3.2 归并排序的非递归版本
- 四、归并排序的特性总结
前言
手撕排序算法第七篇:归并排序!
从本篇文章开始,我会介绍并分析常见的几种排序,例如像插入排序,冒泡排序,希尔排序,选择排序,快速排序,堆排序,归并排序等等!
这篇文章我先来给大家手撕一下归并排序!
大家可以点下面的链接去阅读其他的排序算法:
C语言手撕排序算法
正文开始!
一、常见的排序算法
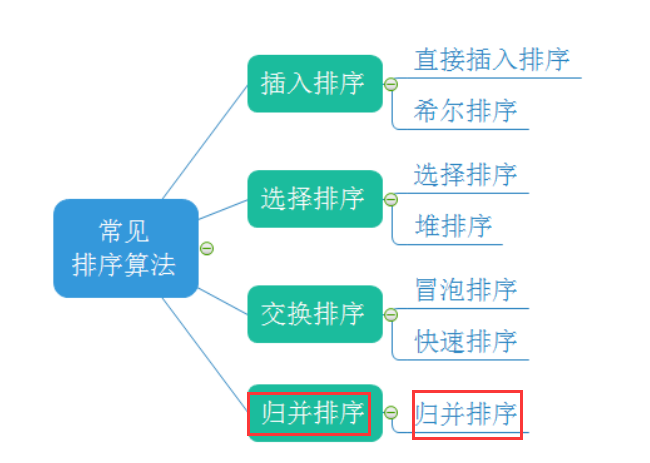
二、归并排序的基本思想
归并排序(MERGE-SORT)是建立在归并操作上的一种有序的排序算法,该算法是采用分治法(Divide and Conquer)是一个非常典型的应用。将已经有序的子序列合并,得到有序的序列;即先使每个子序列有序,再使子序列有序。若将两个有序表合并成一个有序表,称为二路归并。
核心步骤根据图来理解:
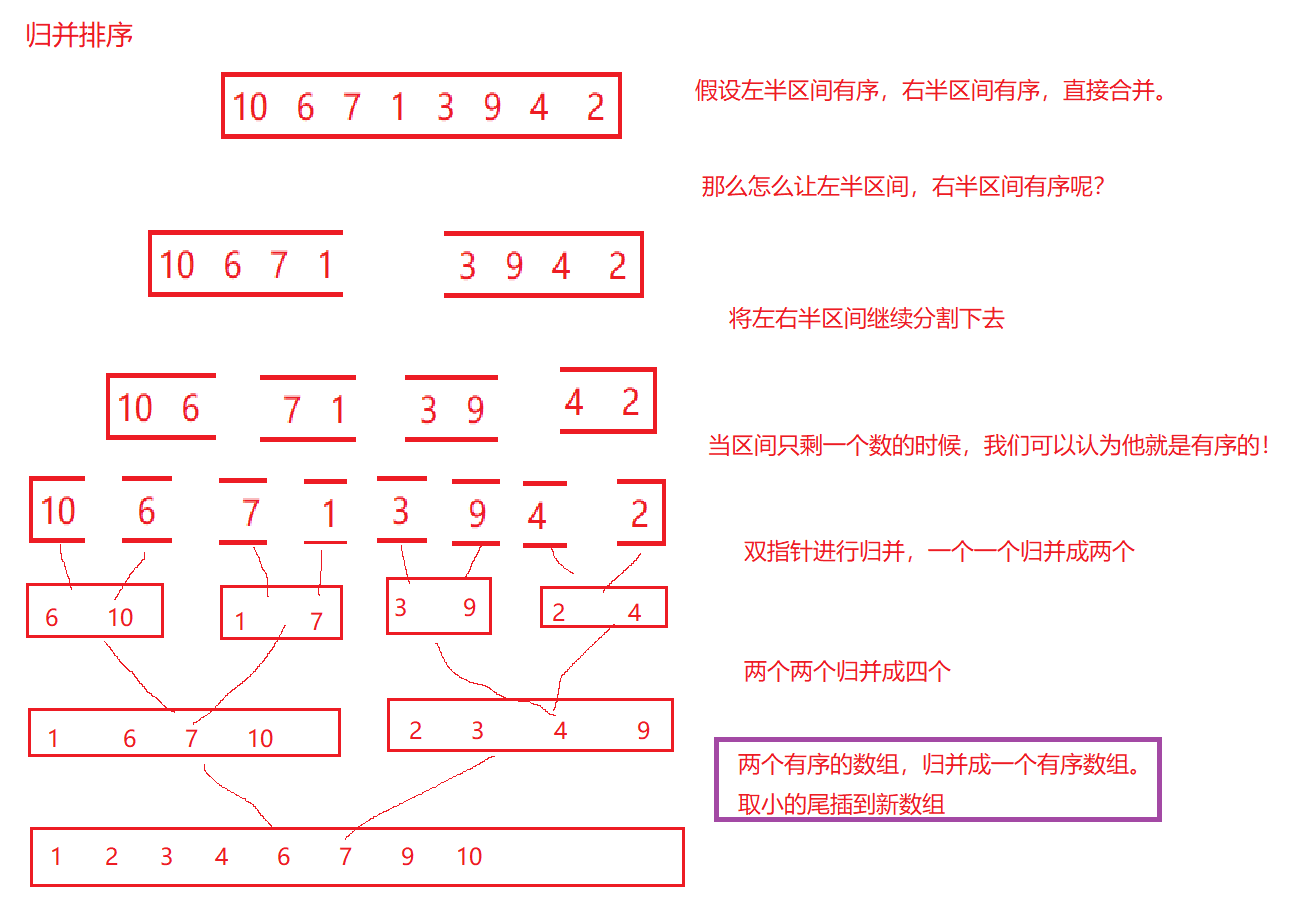
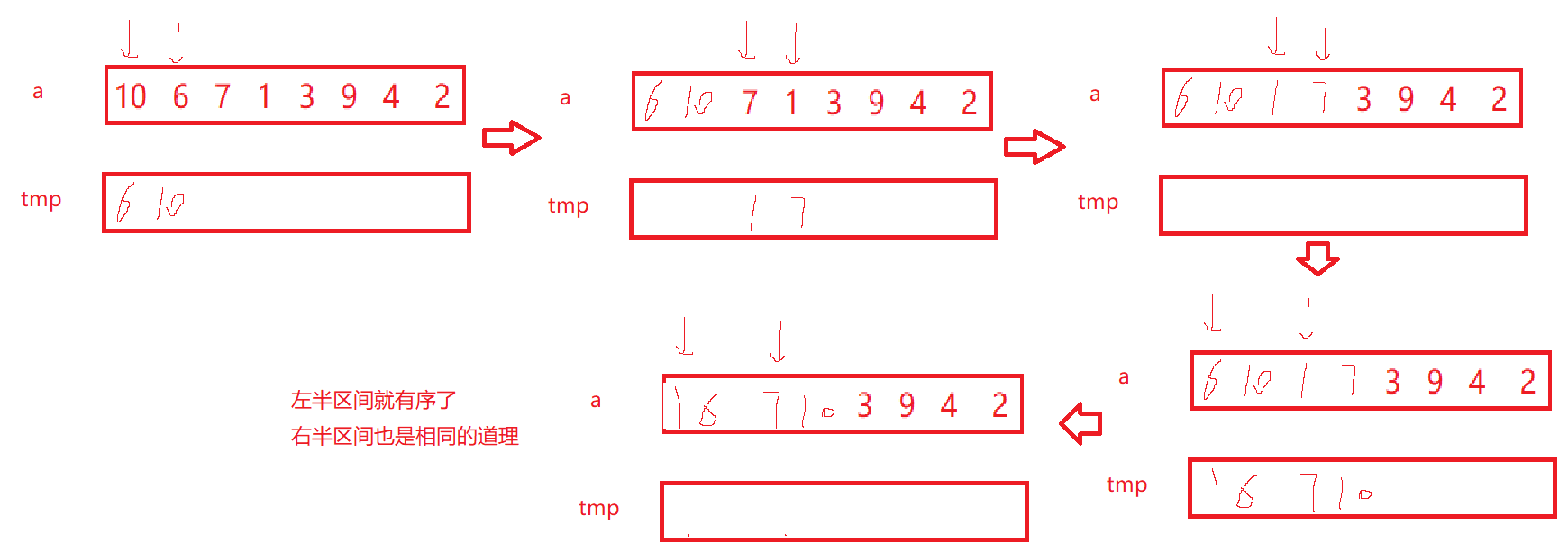
三、归并排序
3.1 归并排序的递归版本
void _MergeSort(int* a,int begin,int end,int* tmp)
{
if (begin >= end)
return;
int mid = (begin + end) >> 1;
//[begin,mid][mid+1,end]
_MergeSort(a,begin,mid,tmp);
_MergeSort(a,mid+1,end,tmp);
//归并[begin,mid][mid+1,end]
int begin1 = begin, end1 = mid;
int begin2 = mid+1, end2 = end;
int index = begin;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[index++] = a[begin1++];
}
else
{
tmp[index++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[index++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[index++] = a[begin2++];
}
//memcpy(a+begin,tmp+begin,(end-begin+1)*sizeof(int));
for (int i = begin; i <= end; i++)
{
a[i] = tmp[i];
}
}
void MergeSort(int* a,int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
assert(tmp);
_MergeSort(a,0,n-1,tmp);
free(tmp);
}
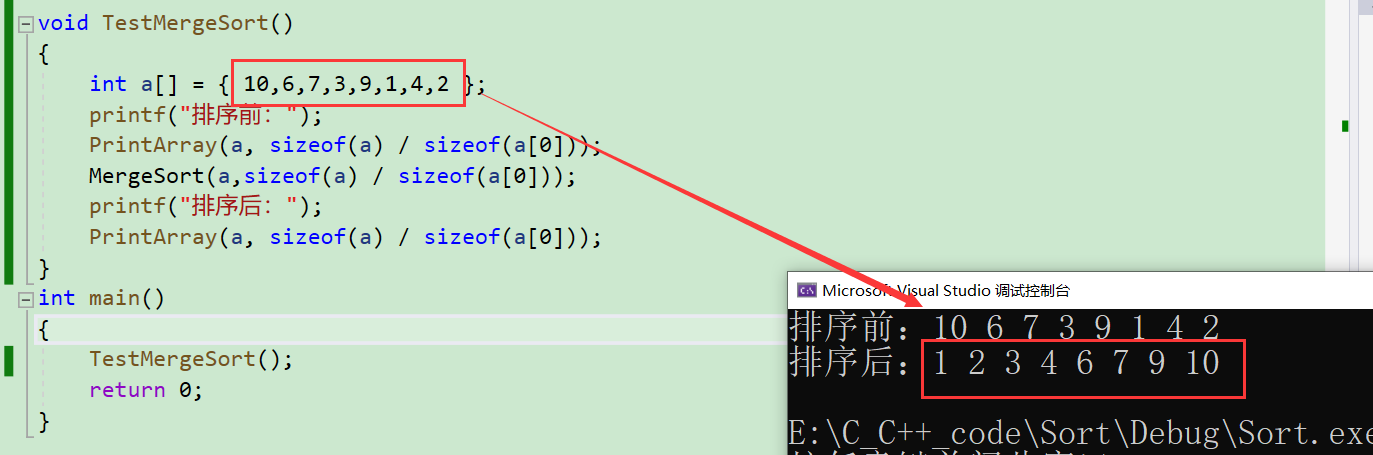
void TestMergeSort()
{
int a[] = { 10,6,7,3,9,1,4,2 };
printf("排序前:");
PrintArray(a, sizeof(a) / sizeof(a[0]));
MergeSort(a,sizeof(a) / sizeof(a[0]));
printf("排序后:");
PrintArray(a, sizeof(a) / sizeof(a[0]));
}
int main()
{
TestMergeSort();
return 0;
}
3.2 归并排序的非递归版本
画图分析如下:
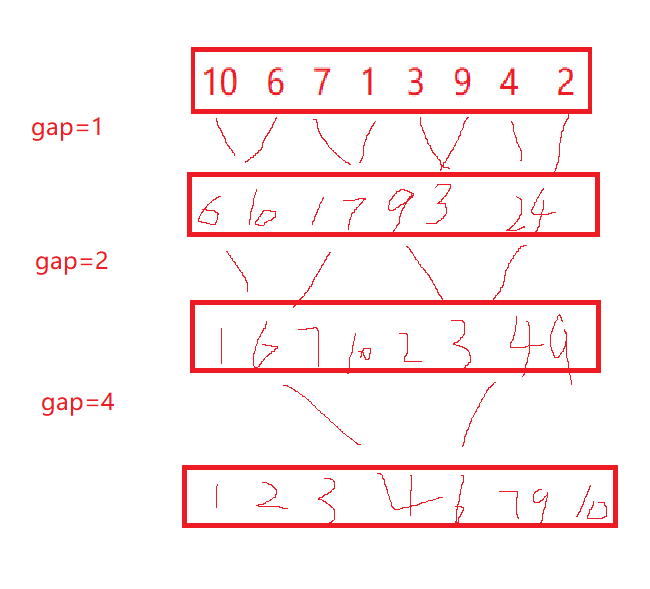
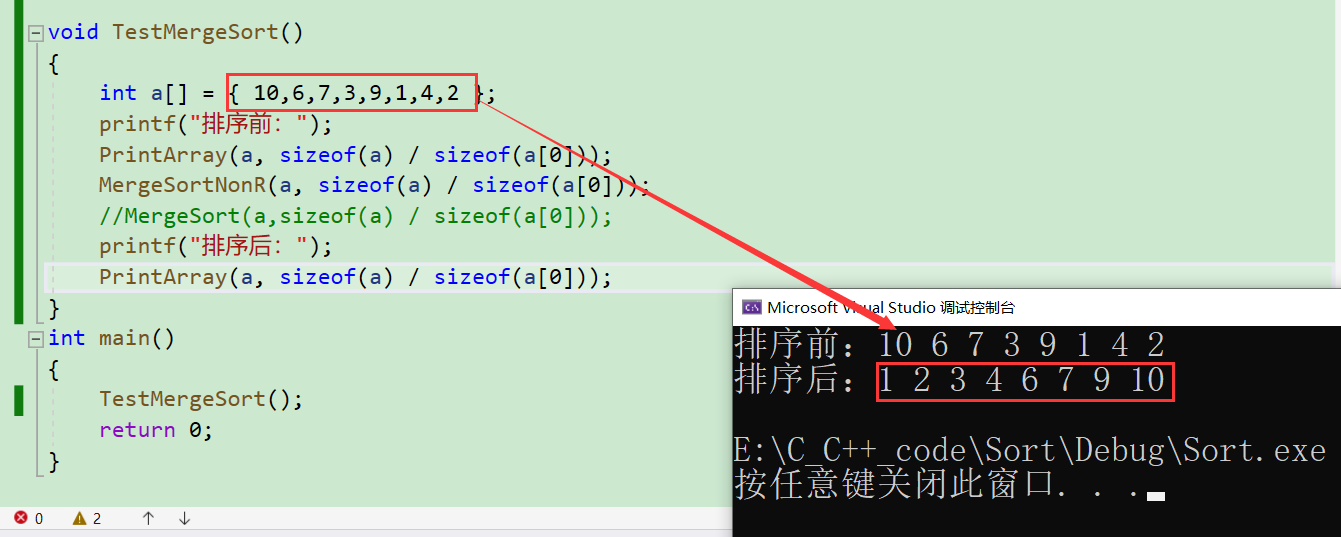
我们可以发现利用上述的思想就可以实现非递归排序。
但是在这里随意加一个数字,程序就崩溃了,这是为什么呢?
先来实验结果:
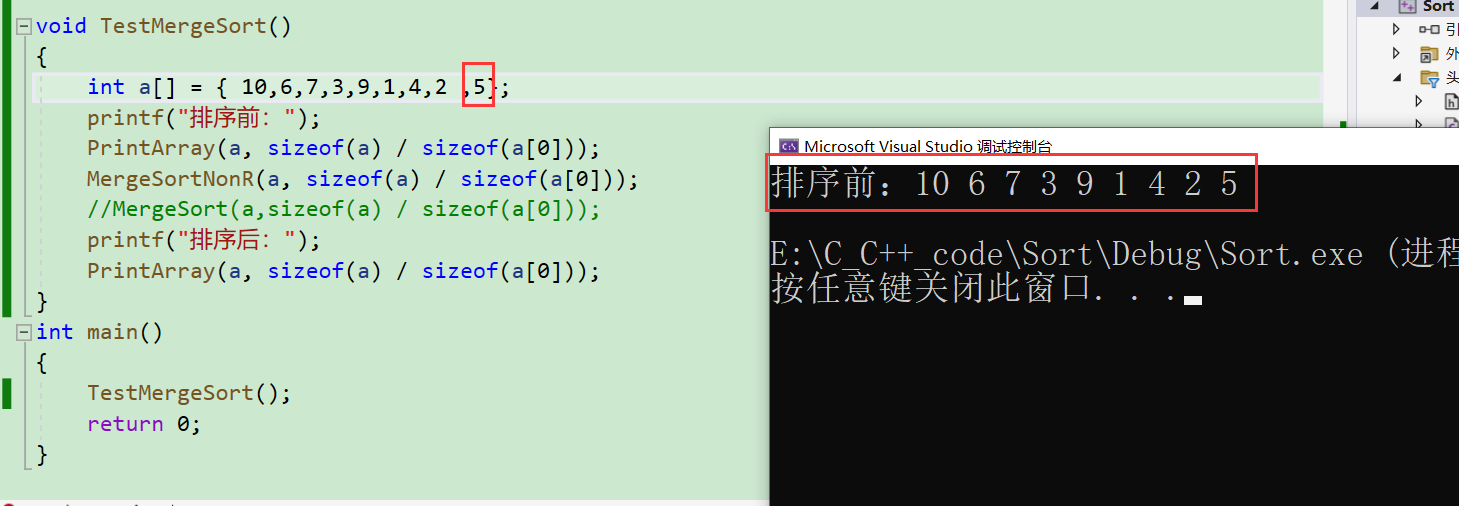
我先利用6个数给大家讲讲,数太多了,分析起来不容易理解!

在这里只有可能end1,begin2,end2可能会越界,所以在归并之前控制约束条件即可!
完整代码如下
//归并排序的非递归版本
void MergeSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
assert(tmp);
int gap = 1;
while (gap<n)
{
//间距为gap的是一组,两两归并
for (int i = 0; i < n; i += 2*gap)
{
int begin1 = i, end1 = i+gap-1;
int begin2 = i+gap, end2 = i+2*gap-1;
int index = i;
//end1越界,修正即可
if (end1 >= n)
{
end1 = n - 1;
}
//begin2越界,证明后半区间不存在
if (begin2 >= n)
{
begin2 = n;
end2 = n-1;
}
//begin2存在,end2越界,修正end2即可
if (begin2 < n && end2 >= n)
{
end2 = n - 1;
}
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[index++] = a[begin1++];
}
else
{
tmp[index++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[index++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[index++] = a[begin2++];
}
}
memcpy(a , tmp , n * sizeof(int));
gap *= 2;
}
free(tmp);
}
void TestMergeSort()
{
int a[] = { 10,6,7,3,9,1};
printf("排序前:");
PrintArray(a, sizeof(a) / sizeof(a[0]));
MergeSortNonR(a, sizeof(a) / sizeof(a[0]));
printf("排序后:");
PrintArray(a, sizeof(a) / sizeof(a[0]));
}
int main()
{
TestMergeSort();
return 0;
}
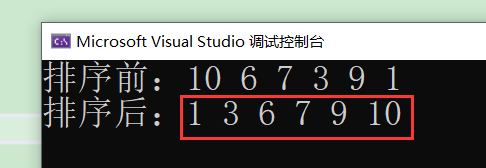
此时归并排序的非递归版本就实现啦!
四、归并排序的特性总结
- 归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多实在解决在磁盘中的外排序问题。
- 时间复杂度:O(N*logN).
- 空间复杂度:O(N).
- 稳定性:稳定.
(本章完!)