链接: 647. 回文子串
链接: 516.最长回文子序列
链接: 动态规划总结

647. 回文子串

理解dp数组的含义很重

class Solution {
    public int countSubstrings(String s) {
        char[] chars = s.toCharArray();
        boolean[][] dp = new boolean[s.length()][s.length()];
        
        int res = 0;
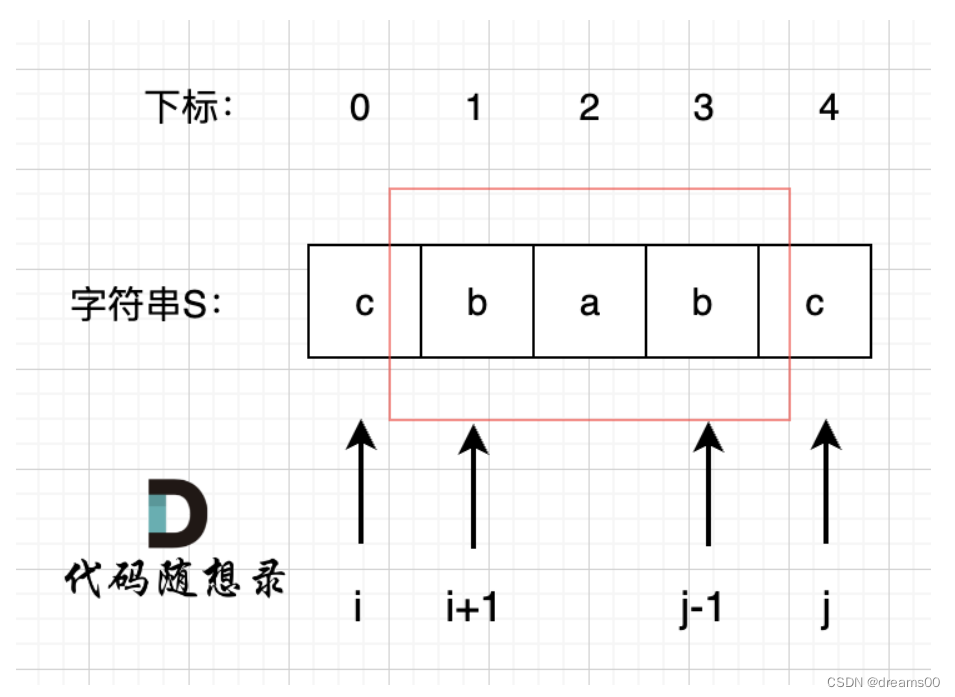
        // 遍历顺序为从下往上，从左往右，为了确保dp[i+1][j-1]首先被遍历到
        for(int i = s.length() - 1; i >= 0; i-- ){
            for(int j = i; j < s.length(); j++){
                if(chars[i] == chars[j]){
                    if(j - i <= 1){// 情况一 和 情况二
                        res++;
                        dp[i][j] = true;
                    }else if(dp[i+1][j-1]){ // 情况三
                        res++;
                        dp[i][j] = true;
                    }
                }
            }
        }

        return res;
    }
}

516.最长回文子序列

class Solution {
    public int longestPalindromeSubseq(String s) {
        int len = s.length();
        int[][] dp = new int[len + 1][len + 1];

        for(int i = len -1; i >= 0; i--){
            dp[i][i] = 1;
            for(int j = i+1; j < len; j++){
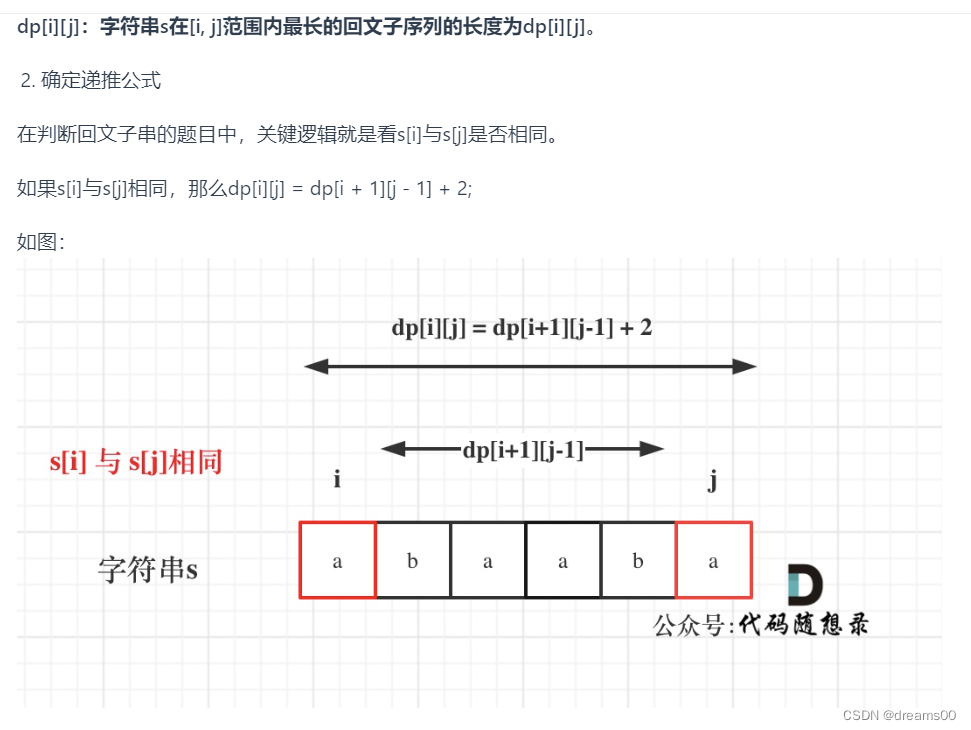
                if(s.charAt(i) == s.charAt(j)){
                    dp[i][j] = dp[i+1][j-1] + 2;
                }else{
                    dp[i][j] = Math.max(Math.max(dp[i][j-1], dp[i+1][j]), dp[i][j]);
                }
            }
        }

        return dp[0][len - 1];
    }
}