2023.9.20

        感觉是目前做过dp题里最难的一题了...

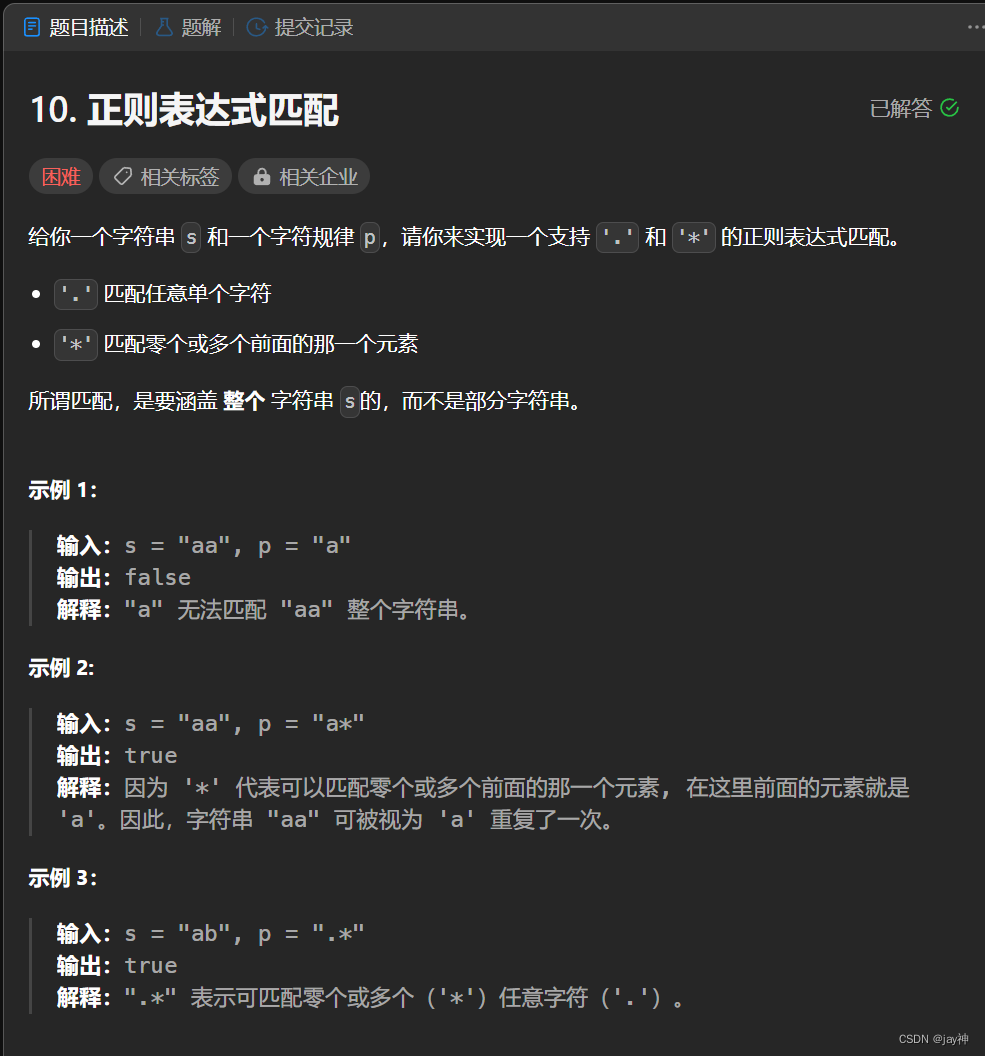
        本题首要的就是需要理解题意，翻了评论区我才发现之前一直理解的题意是错的。 我原来理解的 “ *匹配0次” 是指：*直接消失，不会影响到前面的字符。  但是*和前一个字符其实是连体的，所以说：*如果匹配0次，那么前一个字符就没了，消失了；*如果匹配1次，那么才相当于*消失了，不影响前面的字符；也就是说： *如果匹配n次，相当于前一个字符会出现n次。

        理解了题意之后再来用dp算法做这道题。本题用的是二维bool型dp数组，dp[i][j]含义是：字符串s的前i个字符 和 字符串p的前j个字符 能否匹配。

        再来看核心的递推公式。遍历的时候分为两种情况：

①s和p 的当前字符相等(这个相等包括p的当前字符是“_”,也算一种相等嘛！)：那么可以想象一下，当前这两个字符相等了，像消消乐一样两字符消掉，两个指针各退一步，指向各自的前一个字符，当前dp数组的状态 转化为 之前dp数组的状态。即：dp[i][j] = dp[i - 1][j - 1];

②s和p 的当前字符不相等：两字符不相等了，还有补救措施，那就是p的字符如果为*的话，还有机会匹配。 那么此时又分为两种子情况：

• 当p的当前字符为"*"时：此时需要先判断一下*前面的字符和s的当前字符相不相等。如果不相等，说明*只能带着前面的字符一起消失了，即匹配0个：dp[i][j] = dp[i][j - 2];  如果相等的话：那么*可以匹配0次、也可以匹配1次、也可以匹配多次，即dp[i][j] = dp[i][j - 1] || dp[i][j - 2] || dp[i - 1][j];
• 当p的当前字符不为“*”时：那么直接就是false就行了，不过构建dp数组时是将所有位置都初始化为false了，所以这一步可以省略。

        最后，dp[0][0]需要初始化为true，因为空字符串肯定是能匹配的嘛！ 但是运行的时候有一个案例通不过：s=“aab”，p=“c*a*b” 。 翻看了评论区：有个方法就是分别在s和p之前加个空格：即

        s = " " + s;

        p = " " + p;

        最后上代码：

class Solution {
public:
    bool isMatch(string s, string p) {
        s = " " + s; 
        p = " " + p;
        vector<vector<bool>> dp(s.size() + 1, vector<bool>(p.size() + 1, false));
        dp[0][0] = true;
        for (int i = 1; i <= s.size(); i++) 
        {
            for (int j = 1; j <= p.size(); j++) 
            {
                //字符相同，或者p字符有万能符号。 (万能符号也可以理解为两字符相等)
                if (s[i - 1] == p[j - 1] || p[j - 1] == '.') 
                {
                    dp[i][j] = dp[i - 1][j - 1];
                } 
                else if (p[j - 1] == '*') 
                {
                    if (s[i - 1] == p[j - 2] || p[j - 2] == '.') 
                    {
                        dp[i][j] = dp[i][j - 1] || dp[i][j - 2] || dp[i - 1][j];//分别对应*匹配1次、0次、多次的情况。
                    } 
                    else 
                    {
                        dp[i][j] = dp[i][j - 2]; //p字符串*号前面的字符 和 s字符串当前字符 不相等，只能让*匹配0次。
                    }
                }
            }
        }
        return dp[s.size()][p.size()];
    }
};