一篇文章彻底弄懂单调栈！！！

前言

最近梳理完中间件后荔枝一边学项目一边刷算法，一刷了代码随想录中的字符串、双指针、栈和队列以及单调栈。其中感觉比较有难度的还是单调栈嘿，因此有必要(水)梳理一篇文章来复盘一下单调栈的相关知识~ 希望复盘完后可以有所收获！

文章目录

前言

一、单调栈

二、经典例题

2.1 Leecode739. 每日温度

2.2 Leecode42. 接雨水

2.3 Leecode84. 柱形图中最大的矩形

总结

一、单调栈

相信大家跟荔枝一样都了解过栈这种数据结构吧嘿嘿嘿，栈是一种先进后出的数据结构，在C++中可以使用stack容器适配器来自行选择这种数据结构的底层实现，比如list、vector、deque等。STL默认是采用双端队列Deque来匹配栈的底层的，这里就不过多赘述了。单调栈，顾名思义就是一个单调的栈，它其实就是栈这种数据结构的变种，栈中的元素或按照从小到大顺序排序、或者按照从大到小的顺序排序。也就是说，默认情况下有两种单调栈：单调递增的栈、单调递减的栈。

应用场景：

单调栈一般用在这样的场景：在一组元素nums中，找到任意元素右边第一个最大|小的元素。当然也可以是拿来找左边的。

可能有些小伙伴可能会说：直接暴力出来不就行了，但是直接暴力还是有可能超时滴，单调栈的时间复杂度是O(n)噢。

跟着代码随想录顺序刷，第一道单调栈的题目是Leecode739. 每日温度，这道题目是单调栈系列的模板题，

二、经典例题

2.1 Leecode739. 每日温度

题目描述：

给定一个整数数组 temperatures ，表示每天的温度，返回一个数组 answer ，其中 answer[i] 是指对于第 i 天，下一个更高温度出现在几天后。如果气温在这之后都不会升高，请在该位置用 0 来代替。

输入样例：

temperatures = [73,74,75,71,69,72,76,73]

输出样例：

[1,1,4,2,1,1,0,0]

看完题目，那么我们要选择单调递增的单调栈还是单调递减的单调栈来模拟呢？荔枝觉得还是需要自己手动模拟一下，模拟一遍大概整个实现过程也就了解了。首先荔枝来手动模拟递增的单调栈。

递增单调栈

我们给出一组数据来模拟单调栈解题地过程

首先我们需要定义一个栈来维护记录每一个元素在原容器中的下标，一个vector容器来记录我们需要的结果。在遍历开始之前需要先往stack中push原vector容器template中的第一个元素，这是为了方便后面的比较逻辑。for循环的遍历将从1开始，为了保证栈是单调递增的，如果当前遍历的元素大于stack栈顶元素下标所对应的元素，我们需要将栈顶元素弹出，不过在弹出之前我们可以发现，对于栈顶元素我们要求的最近的最大值其实就是我们当前遍历的元素，根据题目要求的是距离最近的更高温度，那我们就需要实时更新我们的result，因此就有result [stack.top()] = i-stack.top();当前遍历的元素小于或者等于stack栈顶元素下标所对应的元素时，符合单调递增的要求，因此直接push()就可以咯。所以模拟一遍之后我们发现，使用单调递增的单调栈可以用来寻找数组各个元素的右边最近更大元素！

class Solution {
public:
    //单调栈来实现
    vector<int> dailyTemperatures(vector<int>& temperatures) {
        stack<int> stack;
        vector<int> result(temperatures.size(),0);
        //先把头元素加进去
        stack.push(0);
        for(int i=1;i<temperatures.size();i++){
            if(temperatures[i]==temperatures[stack.top()]){
                stack.push(i);
            }else if(temperatures[i]<temperatures[stack.top()]){
                stack.push(i);
            }else{
                while(!stack.empty() && temperatures[i]>temperatures[stack.top()]){
                    result[stack.top()] = i-stack.top();
                    stack.pop();
                }
                stack.push(i);
            }
        }
        return result;
    }
};

递减单调栈

看完递增单调栈的模拟，我们继续试着模拟一下递减单调栈的过程。同样为了保证栈是单调递减的，一次对于每一个遍历的元素i，如果template[i]大于或等于栈顶元素所对应的值，就直接push进栈中即可；如果小于栈顶元素所对应的值，我们需要将栈顶元素弹出，在弹出之前，我们依旧比较容易就可以得出：当前遍历的元素其实就是栈中压着的大于该元素的最近右边最小值！还是比较好理解滴，因为栈中是单调递减的，栈中的某个元素a如果比现在遍历的元素b小，那么在while循环执行完后自然会将a压入b的上方。因此回到上面的题目中，我们得到的result其实是求每个天气的下一个更低温度。

demo示例

class Solution {
public:
    //单调栈来实现
    vector<int> dailyTemperatures(vector<int>& temperatures) {
        stack<int> stack;
        vector<int> result(temperatures.size(),0);
        //先把头元素加进去
        stack.push(0);
        for(int i=1;i<temperatures.size();i++){
            if(temperatures[i]==temperatures[stack.top()]){
                stack.push(i);
            }else if(temperatures[i]>temperatures[stack.top()]){
                stack.push(i);
            }else{
                while(!stack.empty() && temperatures[i]<temperatures[stack.top()]){
                    result[stack.top()] = i-stack.top();
                    stack.pop();
                }
                stack.push(i);
            }
        }
        return result;
    }
};

2.2 Leecode42. 接雨水

题目描述：

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

输入：
height = [0,1,0,2,1,0,1,3,2,1,2,1]

输出
6

要想计算能够接到的雨水的数量，我们必须求出图中蓝色区域对应的长和宽。对于当前遍历的元素，我们以其为依据，分别求出左边和右边的最近更高值，这就回到了上一个问题的场景 —— 每日温度的求解。我们需要注意的是这里对于左边的最近更高值的处理：由于求右边的最近更高值采用的是递增的单调栈，当前遍历的元素如果比栈顶下标所对应的元素更高，那么栈顶下面的元素就可能是我们要求的下一个左边最近更高值。因此我们需要保存栈顶元素并弹出该元素，这样才能得到栈顶下面的元素。

代码示例：

class Solution {
public:
    int trap(vector<int>& height) {
        stack<int> sta;
        sta.push(0);
        int sum = 0;
        for(int i=1;i<height.size();i++){
            if(height[i] < height[sta.top()]){
                sta.push(i);
            }else if(height[i] == height[sta.top()]){
                sta.push(i);
            }else{
                while(!sta.empty() && height[i]>height[sta.top()]){
                    int m = sta.top();
                    sta.pop();
                    if(!sta.empty()){
                        int h = min(height[i],height[sta.top()]) - height[m];
                        int w = i-sta.top()-1;
                        sum += h*w;
                    }
                }
                sta.push(i);
            }
        }
        return sum;

    }
};

demo中其实相对于每日温度改变的其实也比较少哈哈~

2.3 Leecode84. 柱形图中最大的矩形

题目描述：
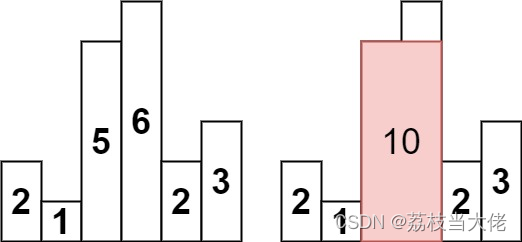
给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

输入：

heights = [2,1,5,6,2,3]

输出：

10

求柱形图中最大矩形其实是一道跟接雨水问题相似的题目，只不过求的是凸起的最大面积，因此我们中间的元素一定是比两侧的大，所以使用的一定是递减的单调栈。区别于接雨水问题，这道题目是以栈顶元素为基准去找左右两边的第一个小于它的数left，right，right-left-1的值就是以该基准轴的高度为主的矩形区域的宽度。而高度一定就是我们现在的基准——栈顶元素，因此这里我们也需要一个变量来记录栈顶元素的大小以及在原数组的下标。

demo示例：

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        //这里需要在前后加上0避免在单调递减栈中阻塞的情况
        stack<int> sta;
        int result = 0;
        heights.insert(heights.begin(),0);
        heights.push_back(0);
        sta.push(0);
        //本题目采用的是单调递减栈
        for(int i=1;i<heights.size();i++){
            if(heights[i]>heights[sta.top()]){
                sta.push(i);
            }else if(heights[i] == heights[sta.top()]){
                sta.push(i);
            }else{  
                while(!sta.empty() && heights[i] < heights[sta.top()]){
                    int mid = sta.top();
                    sta.pop();
                    if(!sta.empty()){
                        int left = sta.top();
                        int right = i;
                        int h = heights[mid];
                        int w = right-left-1;
                        result = max(result,w*h);
                    }
                }
                sta.push(i);
            }
        }
        return result;
    }
};