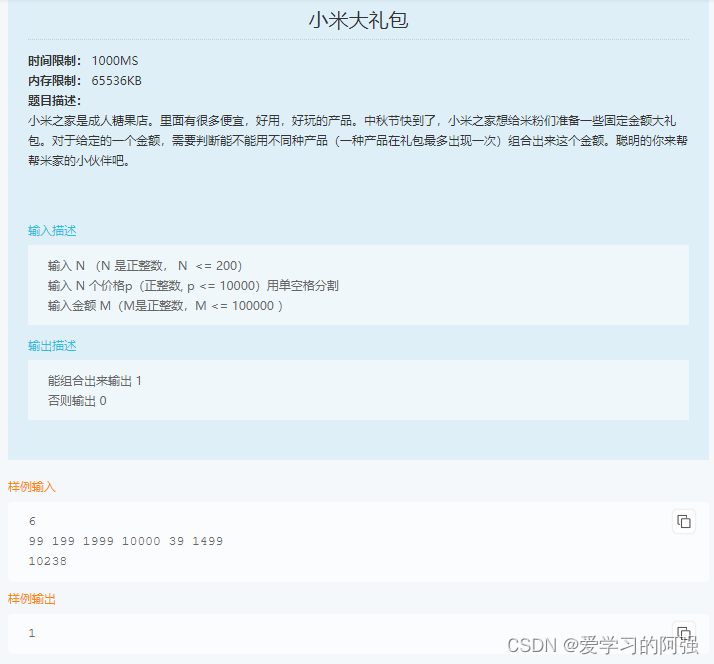
这段代码的主要思路是使用动态规划来构建一个二维数组 dp，其中 dp[i][j] 表示前 i 个产品是否可以组合出金额 j。通过遍历产品列表和可能的目标金额，不断更新 dp 数组中的值，最终返回 dp[N][M] 来判断是否可以组合出目标金额 M。如果 dp[N][M] 为 true，则表示可以组合出目标金额，否则表示无法组合出目标金额。

#include <iostream>
#include <vector>
#include <limits>

using namespace std;


bool miHomeGiftBag(vector<int> p, int M) {
    int N = p.size(); // 获取产品列表中产品的数量
    vector<vector<bool>> dp(N + 1, vector<bool>(M + 1, false)); // 创建一个二维动态规划数组，dp[i][j] 表示前 i 个产品是否能够组合出金额 j
    dp[0][0] = true; // 初始化，金额为0时总是可以组合出来

    for (int i = 1; i <= N; i++) { // 遍历产品列表
        for (int j = 0; j <= M; j++) { // 遍历可能的目标金额
            dp[i][j] = dp[i - 1][j]; // 初始情况，不使用当前产品 i
            if (j - p[i - 1] >= 0) { // 如果当前目标金额 j 大于等于当前产品的价格
                // 尝试使用当前产品 i，判断前 i-1 个产品是否可以组合出目标金额 j - p[i-1]
                dp[i][j] = dp[i - 1][j - p[i - 1]] || dp[i][j];
            }
        }
    }
    return dp[N][M]; // 返回 dp[N][M]，表示前 N 个产品是否可以组合出目标金额 M
}

int main() {
    bool res;

    int _p_size = 0;
    cin >> _p_size;
    cout << _p_size << endl;

    vector<int> _p;
    int _p_item;
    for(int _p_i=0; _p_i<_p_size; _p_i++) {
        cin >> _p_item;
        cin.ignore (std::numeric_limits<std::streamsize>::max(), '\n');
        _p.push_back(_p_item);
    }

    int _M;
    cin >> _M;
    cin.ignore (std::numeric_limits<std::streamsize>::max(), '\n');

    res = miHomeGiftBag(_p, _M);
    cout << res << endl;

    return 0;

}