量子计算基础知识

1.什么是量子计算机？

量子计算机是基于量子力学原理构建的机器，采用了一种新的方法来处理信息，从而使其具有超强的功能。量子计算机使用Qubits处理信息。

2. 什么是量子系统？

一个量子系统指的是由量子力学规则描述和控制的物理系统。在量子力学中，物理系统的状态不再是经典物理中的确定性值，而是由一个称为波函数的数学对象描述的概率分布（粒子的状态不是确定的，而是以概率的形式存在。）。波函数可以用来计算量子系统在不同状态下的概率和测量结果。波函数告诉我们在不同状态下发现粒子的概率，例如它在某个位置的概率或具有某个能量的概率。

一个量子系统可以处于多个态的叠加状态，这与经典物理中的叠加不同。量子叠加的概念意味着在观测之前，系统可以同时处于多个可能的状态，并且这些状态之间会发生干涉。

量子系统的演化是通过薛定谔方程描述的，该方程描述了波函数随时间的变化。通过对量子系统的操作和测量，可以利用量子叠加和纠缠的性质来进行量子计算、量子通信和量子模拟等应用。

量子系统可以由一个或多个量子粒子组成，例如电子、光子或原子等。这些粒子的行为受到量子力学的规则和原理的约束，如叠加原理、量子纠缠和量子态的坍缩等。

2.1 密度矩阵

密度矩阵的引入是为了描述量子系统在纯态和混合态之间的过渡，以及处理涉及量子测量和量子统计的情况。在传统的量子力学中，我们使用波函数来描述系统的态，但当系统处于混合态时，单一的波函数描述不够完整。密度矩阵的引入提供了一种更一般的描述方式，能够同时包含纯态和混合态的信息。

密度矩阵它是一个厄米、正定的矩阵，通常用ρ表示。密度矩阵可以用来描述一个量子系统的状态，无论是处于纯态还是混合态。在纯态情况下，密度矩阵是一个投影矩阵，只有一个非零特征值为1，其余特征值为0。它可以表示系统处于一个确定的量子态，例如一个粒子的自旋向上。在混合态情况下，密度矩阵是一个非投影矩阵，即具有多个非零特征值的矩阵。它可以表示系统处于多个量子态的叠加状态，这些量子态具有一定的概率分布。

密度矩阵不仅包含了量子态的纯度信息，还包含了量子态之间的相干性和相关性信息。通过对密度矩阵的运算，可以计算出各种物理量的期望值，并进一步推导出系统的性质和行为。

3. 噪声中尺度量子NISQ

噪声中的尺度量子是指在量子计算中受到噪声和误差影响的系统。尺度量子通常用于描述量子比特或量子门操作的性能和可靠性。

在实际的量子计算中，量子系统容易受到环境干扰、量子比特之间的耦合、测量误差等各种噪声的影响。这些噪声会导致量子比特的退相干、非理想的量子门操作和测量结果的误差等问题，限制了量子计算的可靠性和精度。

尺度量子考虑的是在噪声影响下的量子计算的尺度和效能。它通常涉及以下几个方面：

量子比特保真度（Fidelity）：量子比特的保真度是指量子比特实际状态与理想状态之间的相似度。在噪声中，保真度衡量了量子比特的退相干程度和受到噪声的影响程度。
量子门操作的保真度：量子门操作是对量子比特进行操作和演化的基本操作。在噪声中，量子门操作的保真度衡量了实际操作与理想操作之间的相似度，即量子门的准确性和精度。
量子纠错：量子纠错是一种技术手段，用于通过特定的算法和编码来纠正量子比特受到的噪声和误差。尺度量子研究中的一项重要任务是设计和优化有效的量子纠错方案，提高量子计算的可靠性和容错性。

3.1 退相干

退想干：量子比特的量子态由一个纯态演化为一个混合态。当量子比特处于纯态时，其量子态可以表示为一个复数的幅度和相位的组合。而当量子比特退相干时，其量子态变为一个混合态，其表示为一组概率分布，其中每个分布对应一个纯态的贡献。这意味着在退相干状态下，量子比特的量子信息和量子叠加态的特性会减弱，而经典概率的影响会增加。

4 量子原生

量子原生是指直接在量子计算机上执行的原始量子操作和量子门操作，而不是将问题转化为经典计算机上的量子模拟或优化算法。量子原生计算强调在量子硬件上使用原生的量子门操作和量子测量，以利用量子计算机的优势来解决特定的问题。

在量子原生计算中，问题的表述和算法设计与量子系统的物理特性密切相关。它可以涉及通过量子逻辑门和量子测量来构建量子电路，使用量子比特的叠加态和纠缠态进行计算，以及利用量子优势来解决特定的问题，如优化、模拟、机器学习等。

量子原生计算的主要优势是它允许直接利用量子计算机的潜力，通过充分利用量子比特之间的量子相互作用和量子叠加的性质，来执行计算和解决问题。这种方法可以在一些特定的应用领域中提供潜在的加速和优势，例如量子化学模拟、优化问题、机器学习等。

然而，量子原生计算也面临着一些挑战，包括量子比特的退相干、量子错误率、噪声和干扰等。解决这些挑战需要设计和优化量子原生算法，开发噪声抑制技术，并利用量子纠错等方法来提高计算的可靠性和稳定性。

5 什么是量子化？

日常生活中，描述一个物体的状态参数基本上都是连续的，比如说爬楼梯时，位于第几层，我们用海拔参数测量，可以测量得出3.3米。因为这些参数可以被分割成更小的部分，3.3米之后还能分的更细，如3.33米、3.333米等等。然而无限分割下去，直到不得不靠几个原子，这种单位去描述物体的长度时，量子效应就出场了。薛定谔方程告诉人们，一定会遇到不可分割的最小单位，这种最小单位统称为量子。这种现象被称为量子化。

量子化是指将经典物理系统或现象转化为符合量子力学规则的描述和处理方式的过程。在经典物理中，我们使用连续的数值来描述物理量，例如位置、速度或能量等。然而，在量子力学中，物理量是以离散的方式存在的，它们的取值被量子化为一系列离散的可能结果。

一个常见的例子是电子的能级。在经典物理中，电子的能量可以是任意值，但在量子物理中，电子的能量是量子化的，只能取特定的离散值，称为能级。当电子从一个能级跃迁到另一个能级时，它的能量变化是不连续的，而是以量子的形式进行跃迁（原子的光谱只会有几个峰值，而不是连续的谱线，这代表了原子内电子的能量，只会出现几种情况，电子不可能具有几种情况之外的中间值，这就叫能量的量子化。）。

6 什么是量子态?什么是态矢？

6.1 量子态的概念

量子态是描述量子系统的状态的概念。在量子力学中，一个物理系统可以处于多个可能的状态之一，而量子态就是描述这个系统所处状态的数学对象。量子态可以同时具有多个可能的状态，而不仅仅是单一的0或1。

量子态通常用波函数来表示。波函数是一个复数函数，它包含了关于量子系统在不同状态下的概率幅。波函数的平方模的平均值给出了观测到系统处于某个状态的概率。

概率幅：用于描述量子系统状态，是一个复数，它与态矢（或波函数）相关联。量子态可以同时具有多个可能的状态，而不仅仅是单一的0或1。概率幅是这些不同状态的复数振幅，用于描述量子比特处于每个可能状态的可能性。当量子比特处于叠加态时，它的量子态可以表示为不同状态的概率幅的叠加。例如，对于一个单量子比特，它可以处于状态和的叠加态，表示为，其中是复数概率幅。这意味着量子比特同时具有成为和两个状态的可能性。
相位：是概率幅的复数部分的角度，它描述了量子态的相对相位差。相位的变化可以影响概率幅的描写，但不会改变测量结果的概率分布。相位差是相对于一个参考相位而言的，通常我们选择参考相位为零。
量子态具有叠加的性质，这意味着系统可以处于多个可能的状态的叠加态。叠加态表示了系统同时具有多个状态的概率分布，直到我们对其进行测量，才能得到一个具体的结果。

通俗来说电子处于不同的能级就说明它处在不同的量子态，这样就可以区分出来不同的量子态。
态矢（State vector），也被称为量子态矢量或量子态，是用于描述量子系统状态的数学对象。在量子力学中，态矢是表示一个物理系统可能的状态的向量。

态矢通常用符号 $∣ ψ ⟩$ 表示，其中 $ψ$ 是一个数学符号，表示量子系统所处的状态。概率幅表示为 $⟨ ψ^{'} ∣ ψ ⟩$ ，其中 $∣ ψ^{'} ⟩$ 表示另一个可能的量子态。这个概率幅的模长的平方，即 $ψ'|ψ⟩|^2$ ，给出了测量时系统从态 $∣ ψ ⟩$ 转变到态 $∣ ψ^{'} ⟩$ 的概率。

6.2 量子态的具体介绍

在量子理论中，描述量子态的向量称为态矢，态矢分为左矢和右矢。
右矢（ket）:
$ψ⟩=[c_1,c_2,...,c_n]^T$
左矢（bra）:
$ψ|=[c_1^*,c_2^*,...,c_n^*]$
采用竖线和尖括号的组合描述一个量子态，其中每一个分量都是复数，右上角标T表示转置。这种形式表示量子态是一个矢量。右矢表示一个n×1的列矢量，左矢表示一个1×n的行矢量。另外，在讨论同一个问题时，如果左矢和右矢在括号内的描述相同的话，那么这两个矢量互为转置共轭。
两个态矢的内积和外积操作如下：
给定任意的两个量子态的矩阵（坐标）表示如下：
$α⟩=[a_1,a_2,...,a_n]^T$
$β⟩=[b_1,b_2,...,b_n]^T$
内积：

$α|β⟩=∑_{i=1}^na_i^* b_i^*$

量子力学中用波函数来描述一个量子态，而内积则是用来计算两个波函数之间的相似度的。内积的结果是一个复数，它描述了两个波函数之间的相似度。如果内积的结果为0，则说明两个波函数是正交的，即它们在空间中没有重叠部分。
外积：
$|α⟩⟨β|={[a_ib_j^*]}_{n*n}=|α⟩\otimes⟨β|$
其中*表示复共轭。

6.3 克罗内克积

A是 $m * n$ 的矩阵，B是 $p * q$ 的矩阵

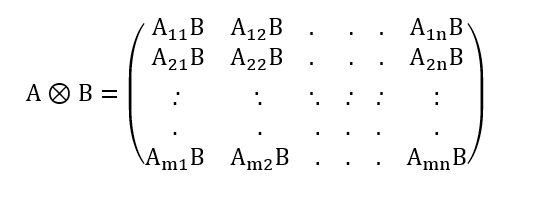
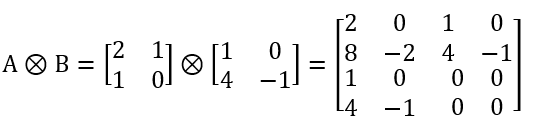
关于个人

An AI algorithm engineer. & open-source enthusiast.

🌱 Currently working in Hefei, China.
💬 If you have any questions about my blog, code, or project, please contact my email: Jakesun2020@163.com or 3895925098qq.com
⭐ Welcome to WeChat official account: 自然语言处理CS
⭐ Welcome to blog: 自然语言处理CS
⭐ Welcome to Zhihu: 自然语言处理CS
⭐ Welcome to QQ group:自然语言处理CS or search for QQ group number: 909675022