课程地址和说明

线性代数实现p4
本系列文章是我学习李沐老师深度学习系列课程的学习笔记，可能会对李沐老师上课没讲到的进行补充。
本节是第二篇

矩阵计算

矩阵的导数运算

此处参考了视频：矩阵的导数运算
为了方便看出区别，我将所有的向量都不按印刷体加粗，而是按手写体在向量对应字母上加箭头的方式展现。

标量方程对向量的导数

在一元函数中，求一个函数的极值点，一般令导数为0（该点切线斜率为0），求得驻点，最后通过极值点定义或推论判断其是否为极值点，也就是如下过程：

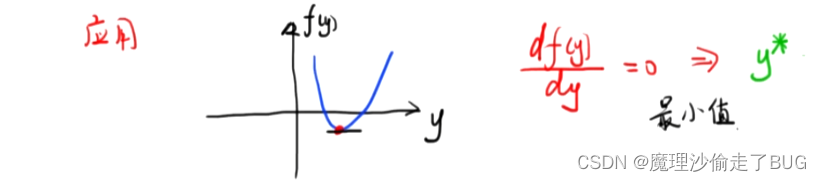
求多元函数极值的方法如下：

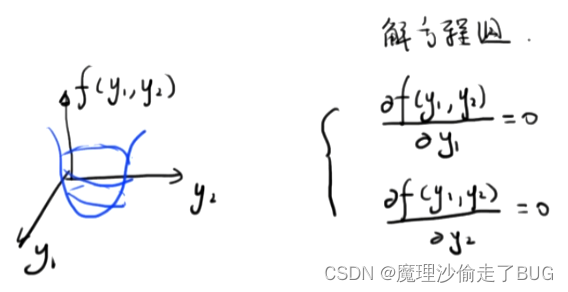
（这个图中给的自变量记成了$y$，实际上记成$x$更顺眼）

• 假设这个多元函数有$m$个变量，即$f(x_1,x_2,...,x_m)$，那么求其极值的偏导数方程组中的方程就有$m$个，这样写起来有一些麻烦，于是我们将用一种简洁的方式表达它，我们将所有这$m$个变量写成一个列向量的形式即$\overrightarrow{x}={\left[\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_m\end{array}\right]}_{m\times 1}$，此时我们将多元函数$f(x_1,x_2,...,x_m)$转化为一个自变量是一个向量的方程即$f(\overrightarrow{x})$
  【注意】此处$\overrightarrow{x}$是一个由多个自变量汇总而成的$m$维列向量（$m\times 1$），而$f(\overrightarrow{x})$是函数值，是一个标量，所以对其求偏导数就是标量对向量求导。

• 此时我们可以定义标量方程对向量的偏导数形式（有两种）为：
  (1)分母布局（Denominator Layout）：
  $$\frac{\partial f(\overrightarrow{x})}{\partial \overrightarrow{x}}={\left[\begin{array}{c}\frac{\partial f(\overrightarrow{x})}{\partial x_1}\\ \frac{\partial f(\overrightarrow{x})}{\partial x_2}\\ ⋮\\ \frac{\partial f(\overrightarrow{x})}{\partial x_m}\end{array}\right]}_{m\times 1}$$
  其中，$\frac{\partial f(\overrightarrow{x})}{\partial \overrightarrow{x}}$为$m\times 1$的列向量。
  (2)分子布局（Numerator Layout）：
  $$\frac{\partial f(\overrightarrow{x})}{\partial \overrightarrow{x}}={\left[\begin{array}{cccc}\frac{\partial f(\overrightarrow{x})}{\partial x_1},& \frac{\partial f(\overrightarrow{x})}{\partial x_2},& \dots ,& \frac{\partial f(\overrightarrow{x})}{\partial x_m}\end{array}\right]}_{1\times m}$$
  其中，$\frac{\partial f(\overrightarrow{x})}{\partial \overrightarrow{x}}$为$1\times m$的行向量。
  不同的资料采用的布局不一样，分子布局与分母布局互为转置，虽然在李沐老师的课程中标量对向量的导数采用了分子布局，但是为了方便推导一些结论，我们采用分母布局，注意分母布局和分子布局的结论互为转置。

• 【例】已知$f(x_1,x_2)=x_1^2+x_2^2$，其中$\overrightarrow{x}=\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]$，求$\frac{\partial f(\overrightarrow{x})}{\partial \overrightarrow{x}}$
  【答】$\frac{\partial f(\overrightarrow{x})}{\partial \overrightarrow{x}}=\left[\begin{array}{c}\frac{\partial f(\overrightarrow{x})}{\partial x_1}\\ \frac{\partial f(\overrightarrow{x})}{\partial x_2}\end{array}\right]=\left[\begin{array}{c}2x_1\\ 2x_2\end{array}\right]$

向量方程对向量的导数

设有如下函数，它本身就是一个向量，然后它的自变量也是向量（由多个自变量组成的向量），即：
$$\overrightarrow{f}(\overrightarrow{x})={\left[\begin{array}{c}{f}_1(\overrightarrow{x})\\ f_2(\overrightarrow{x})\\ ⋮\\ f_n(\overrightarrow{x})\end{array}\right]}_{n\times 1},\overrightarrow{x}=\left[\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_m\end{array}\right]$$
其中，$\overrightarrow{f}(\overrightarrow{x})$是一个$n\times 1$的列向量，$\overrightarrow{x}$是一个$m\times 1$的列向量。
此时我们将其偏导数形式定义为：

• (1)分母布局：
  $$\frac{\partial {\overrightarrow{f}(\overrightarrow{x})}_{n\times 1}}{\partial {\overrightarrow{x}}_{m\times 1}}=\left[\begin{array}{c}\frac{\partial f(\overrightarrow{x})}{\partial x_1}\\ \frac{\partial f(\overrightarrow{x})}{\partial x_2}\\ ⋮\\ \frac{\partial f(\overrightarrow{x})}{\partial x_m}\end{array}\right]={\left[\begin{array}{cccc}\frac{\partial f_1(\overrightarrow{x})}{\partial x_1}& \frac{\partial f_2(\overrightarrow{x})}{\partial x_1}& \dots & \frac{\partial f_n(\overrightarrow{x})}{\partial x_1}\\ \frac{\partial f_1(\overrightarrow{x})}{\partial x_2}& \frac{\partial f_2(\overrightarrow{x})}{\partial x_2}& \dots & \frac{\partial f_n(\overrightarrow{x})}{\partial x_2}\\ ⋮& ⋮& \ddots & ⋮\\ \frac{\partial f_1(\overrightarrow{x})}{\partial x_m}& \frac{\partial f_2(\overrightarrow{x})}{\partial x_m}& \dots & \frac{\partial f_n(\overrightarrow{x})}{\partial x_m}\end{array}\right]}_{m\times n}$$
  (2)分子布局：
  $$\frac{\partial {\overrightarrow{f}(\overrightarrow{x})}_{n\times 1}}{\partial {\overrightarrow{x}}_{m\times 1}}=\left[\begin{array}{c}\frac{\partial f_1(\overrightarrow{x})}{\partial \overrightarrow{x}}\\ \frac{\partial f_2(\overrightarrow{x})}{\partial \overrightarrow{x}}\\ \dots \\ \frac{\partial f_n(\overrightarrow{x})}{\partial \overrightarrow{x}}\end{array}\right]={\left[\begin{array}{cccc}\frac{\partial f_1(\overrightarrow{x})}{\partial x_1}& \frac{\partial f_1(\overrightarrow{x})}{\partial x_2}& \dots & \frac{\partial f_1(\overrightarrow{x})}{\partial x_m}\\ \frac{\partial f_2(\overrightarrow{x})}{\partial x_1}& \frac{\partial f_2(\overrightarrow{x})}{\partial x_2}& \dots & \frac{\partial f_2(\overrightarrow{x})}{\partial x_m}\\ ⋮& ⋮& \ddots & ⋮\\ \frac{\partial f_n(\overrightarrow{x})}{\partial x_1}& \frac{\partial f_n(\overrightarrow{x})}{\partial x_2}& \dots & \frac{\partial f_n(\overrightarrow{x})}{\partial x_m}\end{array}\right]}_{n\times m}$$

• 【例】已知$\overrightarrow{f}(\overrightarrow{x})=\left[\begin{array}{c}{f}_1(\overrightarrow{x})\\ f_2(\overrightarrow{x})\end{array}\right]={\left[\begin{array}{c}{x}_1^2+x_2^2+x_3\\ x_3^2+2x_1\end{array}\right]}_{2\times 1}$，$\overrightarrow{x}=\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right]$，求$\frac{\partial \overrightarrow{f}(\overrightarrow{x})}{\partial \overrightarrow{x}}$
  【答】按分母布局：$\frac{\partial \overrightarrow{f}(\overrightarrow{x})}{\partial \overrightarrow{x}}=\left[\begin{array}{c}\frac{\partial f(\overrightarrow{x})}{\partial x_1}\\ \frac{\partial f(\overrightarrow{x})}{\partial x_2}\\ \frac{\partial f(\overrightarrow{x})}{\partial x_3}\end{array}\right]=\left[\begin{array}{cc}\frac{\partial f_1(\overrightarrow{x})}{\partial x_1}& \frac{\partial f_2(\overrightarrow{x})}{\partial x_1}\\ \frac{\partial f_1(\overrightarrow{x})}{\partial x_2}& \frac{\partial f_2(\overrightarrow{x})}{\partial x_2}\\ \frac{\partial f_1(\overrightarrow{x})}{\partial x_3}& \frac{\partial f_2(\overrightarrow{x})}{\partial x_3}\end{array}\right]=\left[\begin{array}{cc}2x_1& 2\\ 2x_2& 0\\ 1& 2x_3\end{array}\right]$
  按分子布局：$\frac{\partial \overrightarrow{f}(\overrightarrow{x})}{\partial \overrightarrow{x}}=\left[\begin{array}{c}\frac{\partial f_1(\overrightarrow{x})}{\partial \overrightarrow{x}}\\ \frac{\partial f_2(\overrightarrow{x})}{\partial \overrightarrow{x}}\end{array}\right]=\left[\begin{array}{ccc}\frac{\partial f_1(\overrightarrow{x})}{\partial x_1}& \frac{\partial f_1(\overrightarrow{x})}{\partial x_2}& \frac{\partial f_1(\overrightarrow{x})}{\partial x_3}\\ \frac{\partial f_2(\overrightarrow{x})}{\partial x_1}& \frac{\partial f_2(\overrightarrow{x})}{\partial x_2}& \frac{\partial f_2(\overrightarrow{x})}{\partial x_3}\end{array}\right]=\left[\begin{array}{ccc}2x_1& 2x_2& 1\\ 2& 0& 2x_3\end{array}\right]$